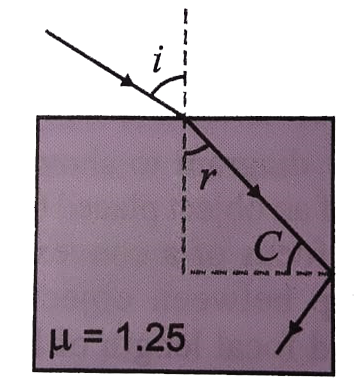
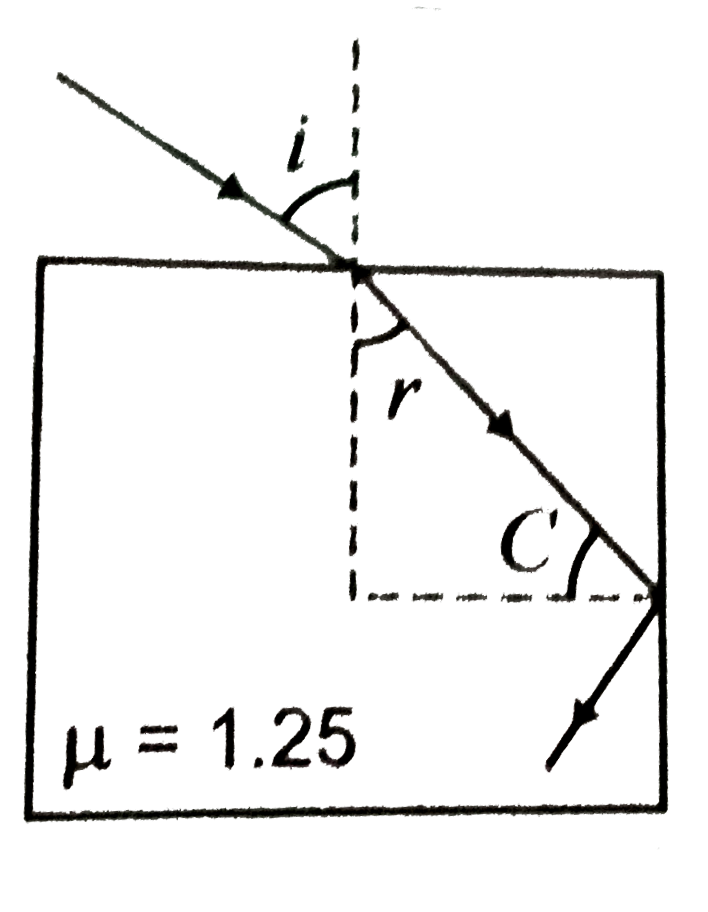
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is
cos−1(34)
sin−1(34)
tan−1(34)
cot−1(34)
The correct Answer is:B
Let the light sufferes total internal reflection at the vertical surface where the critical angle is θc as shown in Fig.

sinθc=μ1μ2=11.25=45
Here, θ1=90∘−θc
so sinθ1=sin90∘−θc=cosθc=35
For refraction at the horizontal surface
μ1μ2=sinθsinθ1
or 1.251=sinθ3/5
or sinθ=35×1.25=34
or θ=sin−1(3/4)
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Problems for practice
Explore 4 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Comprehension 1
Explore 1 Video
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Value based questions
Explore 3 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
Knowledge Check
For a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.
 A1.732B1.5C1.31D1.6
A1.732B1.5C1.31D1.6A ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
Asin−1(Iμ)Btan−1(1μ)Csin−1(μ−1μ)Dcos−1(1μ)In the diagram shown a ray of light is incidetn on the interface between1&2at angle slightly greater than critical angle.The light suffers total internal reflections at this surface .After that the light ray falls at the interface at this interface .After that the light ray falls at the interface reflection..Which of the following relations should hold true?
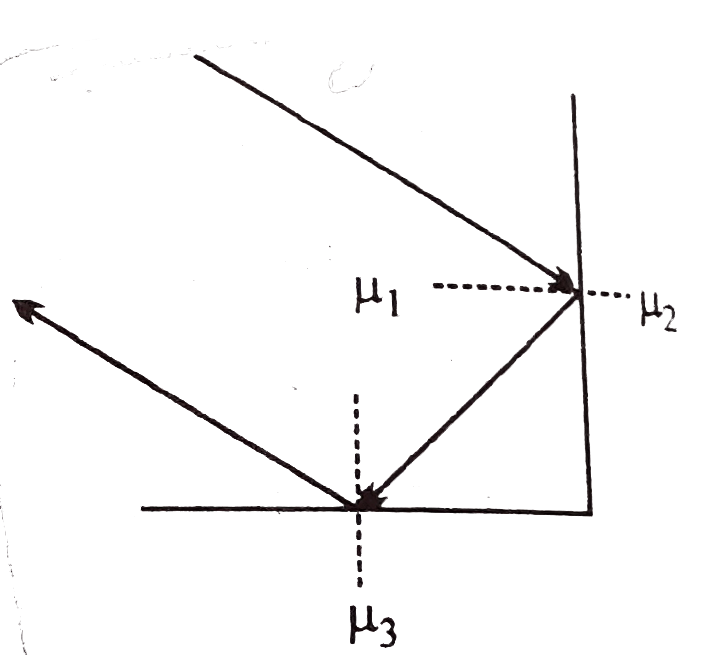 Aμ1<μ2<μ3Bμ21−μ22<μ23Cμ21−μ32<μ22Dμ21+μ22<μ23
Aμ1<μ2<μ3Bμ21−μ22<μ23Cμ21−μ32<μ22Dμ21+μ22<μ23
In Fig. find the maximum angle i for which light suffers total internal reflection at the vertical surface.
View SolutionA light rays is incident on a prism of prism angle A and refractive index μ. Show that the smallest value of the angle of incidence for which the reflected ray does not suffer total internal reflection at the second face, i.e. just comes out of it, is given by
i=sin−1[(μ2−1)1/2sinA−cosA].
View SolutionIn the figure shown for an angle of incidence i at the top of the surface, what is the minimum refractive index for total internal reflection at the vertical surface.
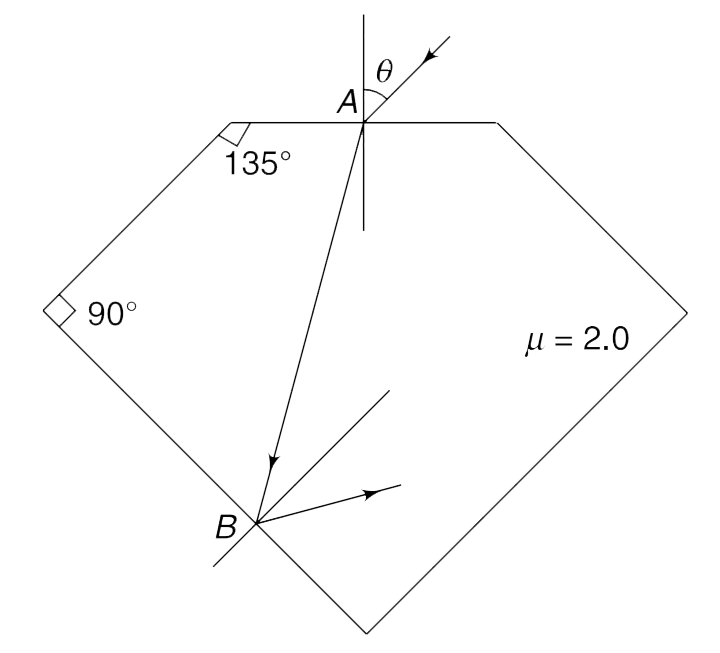
View SolutionLight is incident at point A on one of the faces of a diamond crystal (μ=2.0). Find the maximum allowed value of angle of incidence θ so that light suffers total internal reflection at point B.
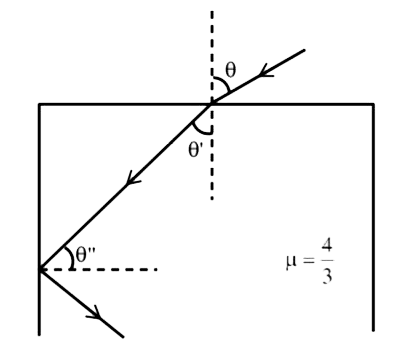
View SolutionA ray of light entering from air into a denser medium of refractive index 43, as shown in figure
The light ray suffers total internal reflection at the adjacent surface as shown. The maximum value of angle θ should be equal to :
View Solution


 .
.