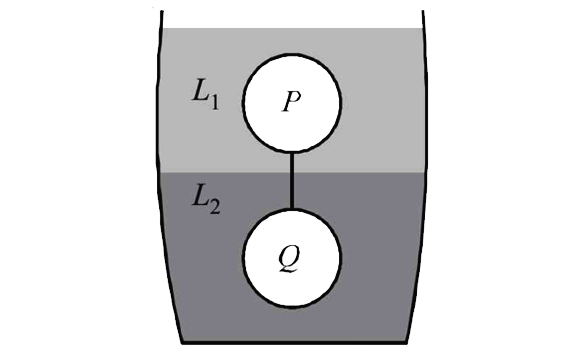
Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut(see figure). If sphere P alone in L2 has terminal velocity →Vp and Q alone in L1 has terminal velocity →VQ, then
∣∣∣vPvQ∣∣∣=η1η2
→vP→vQ=η2η1
→vP.→vQ>0
→vP.→vQ<0
The correct Answer is:B, D
As terminal velocity v=2r2(ρ−σ)g9η
where ρ,σ be the density of spherical body of radius r and density of liquid respectively. η is the coefficient of viscosity of liquid. Then 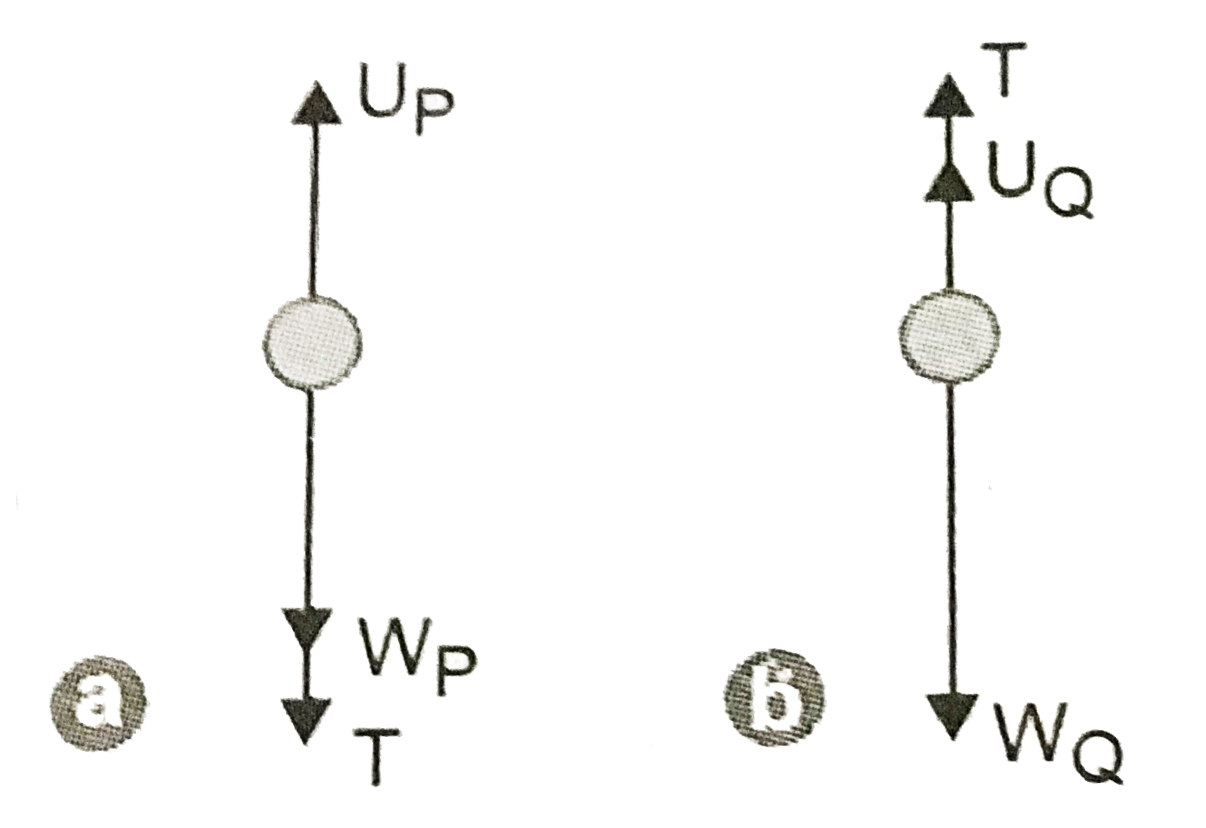
v∝(ρ−σ)η
As per question, if sphere P alone is in liquid L2 has terminal velocity →vP and Q alone in liquid L1 has terminal velocity →vQ, then
vPvQ=(ρ1−σ2)/η1(ρ2−σ1)/η2=(ρ1−σ2)/η2(ρ2−σ1)/η1 .....(i)
As the system is floating in equilibrium. Let UP,UQ are the upthrust on P and Q respectively.
UP−WP=T=WQ−UQ
or UP+UQ=WP+WQ
or σ1Vg+σ2Vg=ρ1Vg+ρ2Vg
or σ1+σ2=ρ1+ρ2 or ρ1−σ2=σ1−ρ2 .....(ii)
From (i) and (ii) ,vpvQ=−η2η1 or |→vP|∣∣→vQ∣∣=|η2|η1∣
∴ option (b) is true.
As →vP and →vQ are of opposite sign
∴→vP.→vQ<0 . Thuse, option (d) is corrected.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
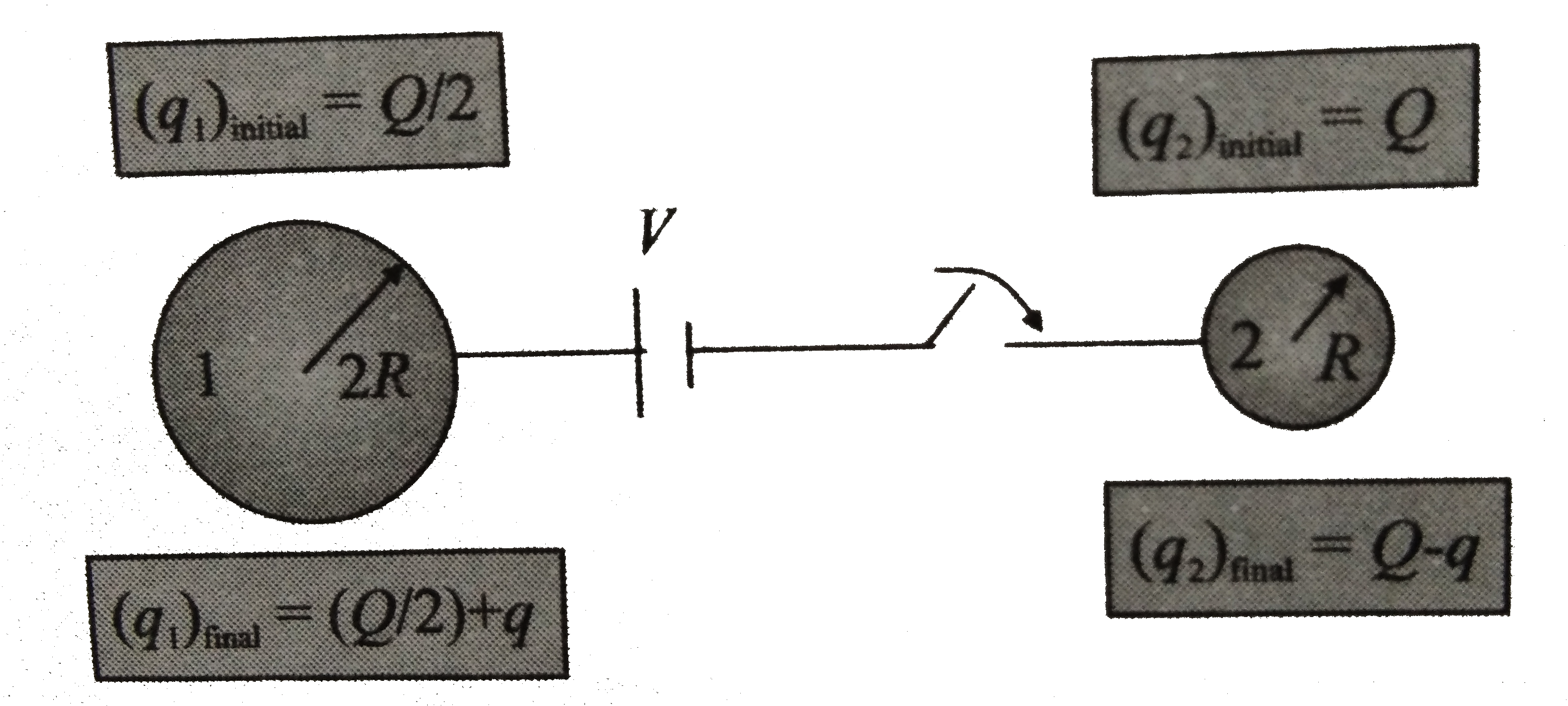
There are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
View SolutionConsider two solid spheres P and Q each of density 8gmcm−3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gmcm−3 and viscosity η=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm−3 and viscosity η=2 poiseulles. The ratio of the terminal velocities of P and Q is
View Solution
Knowledge Check
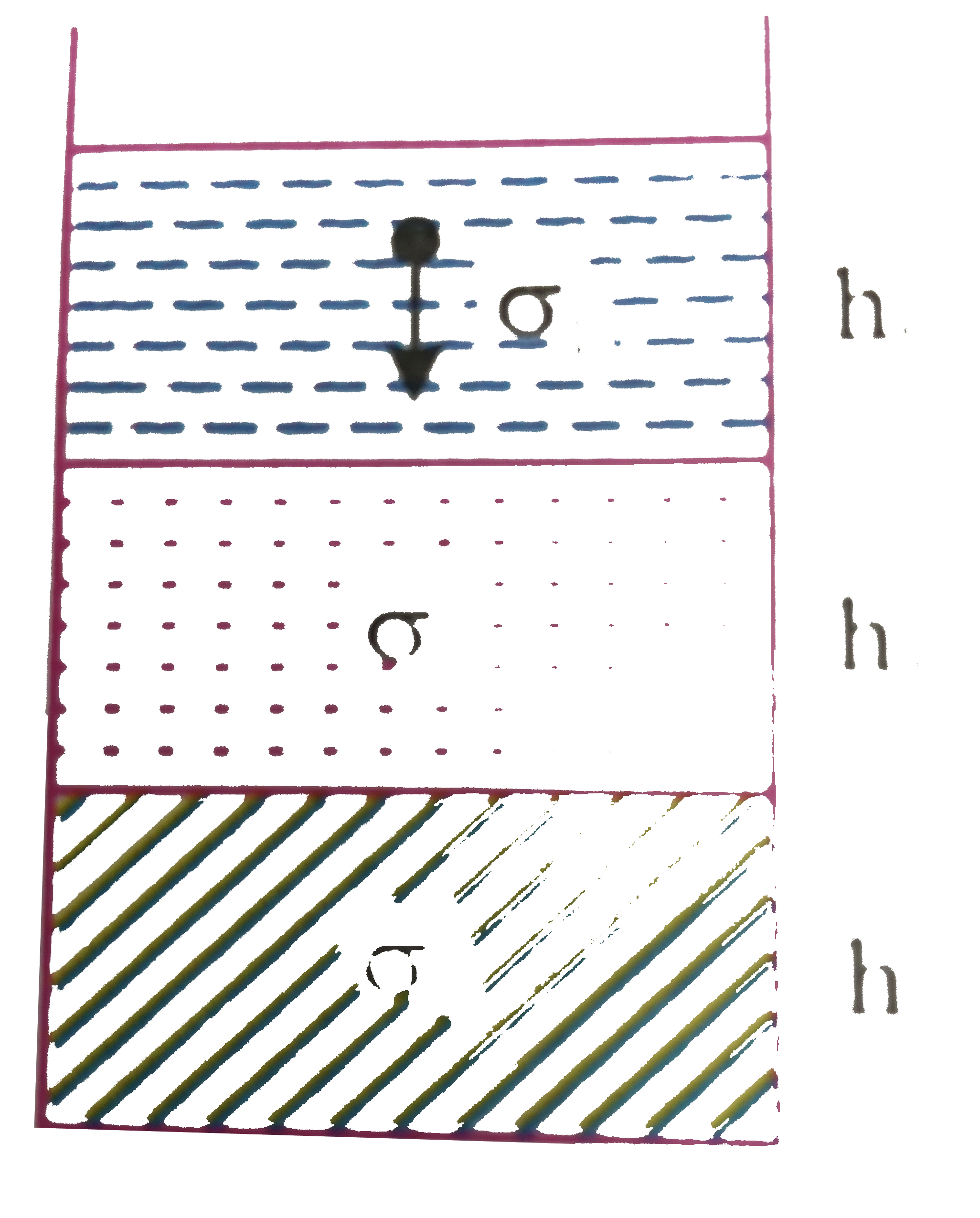
A ball moves successively through three liquids, at rest as shown, of densities σ1,σ2 and σ3 and viscosity coefficient η1,η2 and η3 and respectively with the same terminal velocity thenAη3>η2>η1Bσ1η1=σ2η2=σ3η3Cη1η3>η3η2Dη2σ1−η1σ2η3σ1−η1σ3=η2−η1η3−η1Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1Two wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
Aρ1l1+ρ2l2l1+l2Bρ1l2+ρ2l1l1−l2Cρ1l2+ρ2l1l1+l2Dρ1l1+ρ2l2l1−l2
The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo wires of same radius having lengths l1, and l2 and resistivities ρ1 and ρ2 are connected in series. The equivalent resistivity will be
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo wires of equal diameters of resistivies ρ1 and ρ2 and lengths l and l respectively are joined in series. The equivalent resistivity of the combination is
View SolutionTwo spherical conductors of radii R1andR2 are separated by a distance much larger than the radius of eighter sphere. The spheres are connected by a conducting wire as shown in (Fig. 3.128). If the charges on the spheres in equilibrium are q1andq2, respectively, what is the ratio of the field strength at the surfaces of the spheres ?
 .
.
View Solution
