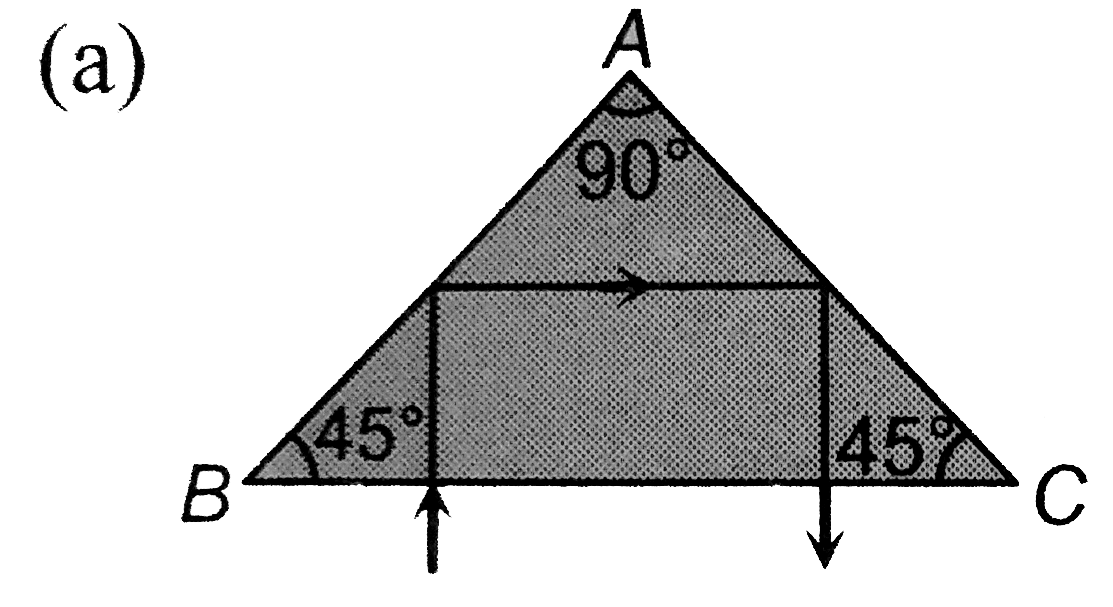
The refractive index of a material of a prism of angles 45∘−45∘−90∘ is 1.5. The path of the ray of light incident normally on the hypotenuse side is shown in


The correct Answer is:A
To solve the problem, we need to analyze the path of a ray of light incident normally on the hypotenuse of a prism with angles 45°, 45°, and 90° and a refractive index of 1.5. We will also check for total internal reflection (TIR) conditions.
1. Identify the Prism and Its Properties:
- The prism has angles of 45°, 45°, and 90°.
- The refractive index (μ) of the prism material is given as 1.5.
2. Determine the Critical Angle (C):
- The critical angle can be calculated using the formula:
sinC=1μ
- Substituting the value of μ:
sinC=11.5=23
- Therefore, the critical angle C is:
C=sin−1(23)
3. Calculate the Value of the Critical Angle:
- Using a calculator or trigonometric tables, we find:
C≈41.81∘
- This value is less than 45°, which is the angle of incidence on the prism's hypotenuse.
4. Analyze the Incident Ray:
- Since the ray is incident normally on the hypotenuse, the angle of incidence i is 0°.
- The angle of refraction r can be calculated using Snell's law:
n1sini=n2sinr
- Here, n1=1 (air), n2=1.5, and i=0°:
1⋅sin(0)=1.5⋅sinr⟹sinr=0⟹r=0°
- The ray will pass straight into the prism without bending.
5. Refraction at the Other Surface:
- When the ray reaches the second surface of the prism (the 45° angle), the angle of incidence is 45°.
- We need to check if this angle is greater than the critical angle:
- Since 45°>41.81°, TIR will occur.
6. Total Internal Reflection:
- The ray will undergo total internal reflection at the 45° surface.
- The angle of reflection will also be 45°.
7. Path of the Ray:
- After reflecting off the 45° surface, the ray will exit the prism through the hypotenuse.
- The angle of incidence at the hypotenuse will again be 45°, which is greater than the critical angle, leading to TIR.
8. Final Path:
- The ray will reflect off the 45° surface and exit the prism at an angle of 45° with respect to the normal at the hypotenuse.
Conclusion:
The path of the ray of light incident normally on the hypotenuse of the prism will undergo total internal reflection at the 45° surfaces and exit at an angle of 45°.
- The prism has angles of 45°, 45°, and 90°.
- The refractive index (μ) of the prism material is given as 1.5.
- The critical angle can be calculated using the formula:
sinC=1μ
- Substituting the value of μ:
sinC=11.5=23
- Therefore, the critical angle C is:
C=sin−1(23)
- Using a calculator or trigonometric tables, we find:
C≈41.81∘
- This value is less than 45°, which is the angle of incidence on the prism's hypotenuse.
- Since the ray is incident normally on the hypotenuse, the angle of incidence i is 0°.
- The angle of refraction r can be calculated using Snell's law:
n1sini=n2sinr
- Here, n1=1 (air), n2=1.5, and i=0°:
1⋅sin(0)=1.5⋅sinr⟹sinr=0⟹r=0°
- The ray will pass straight into the prism without bending.
- When the ray reaches the second surface of the prism (the 45° angle), the angle of incidence is 45°.
- We need to check if this angle is greater than the critical angle:
- Since 45°>41.81°, TIR will occur.
- The ray will undergo total internal reflection at the 45° surface.
- The angle of reflection will also be 45°.
- After reflecting off the 45° surface, the ray will exit the prism through the hypotenuse.
- The angle of incidence at the hypotenuse will again be 45°, which is greater than the critical angle, leading to TIR.
- The ray will reflect off the 45° surface and exit the prism at an angle of 45° with respect to the normal at the hypotenuse.
The path of the ray of light incident normally on the hypotenuse of the prism will undergo total internal reflection at the 45° surfaces and exit at an angle of 45°.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Optical Instruments
55 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Problems Based On Mixed Concepts
37 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Refraction At Curved Surface
64 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
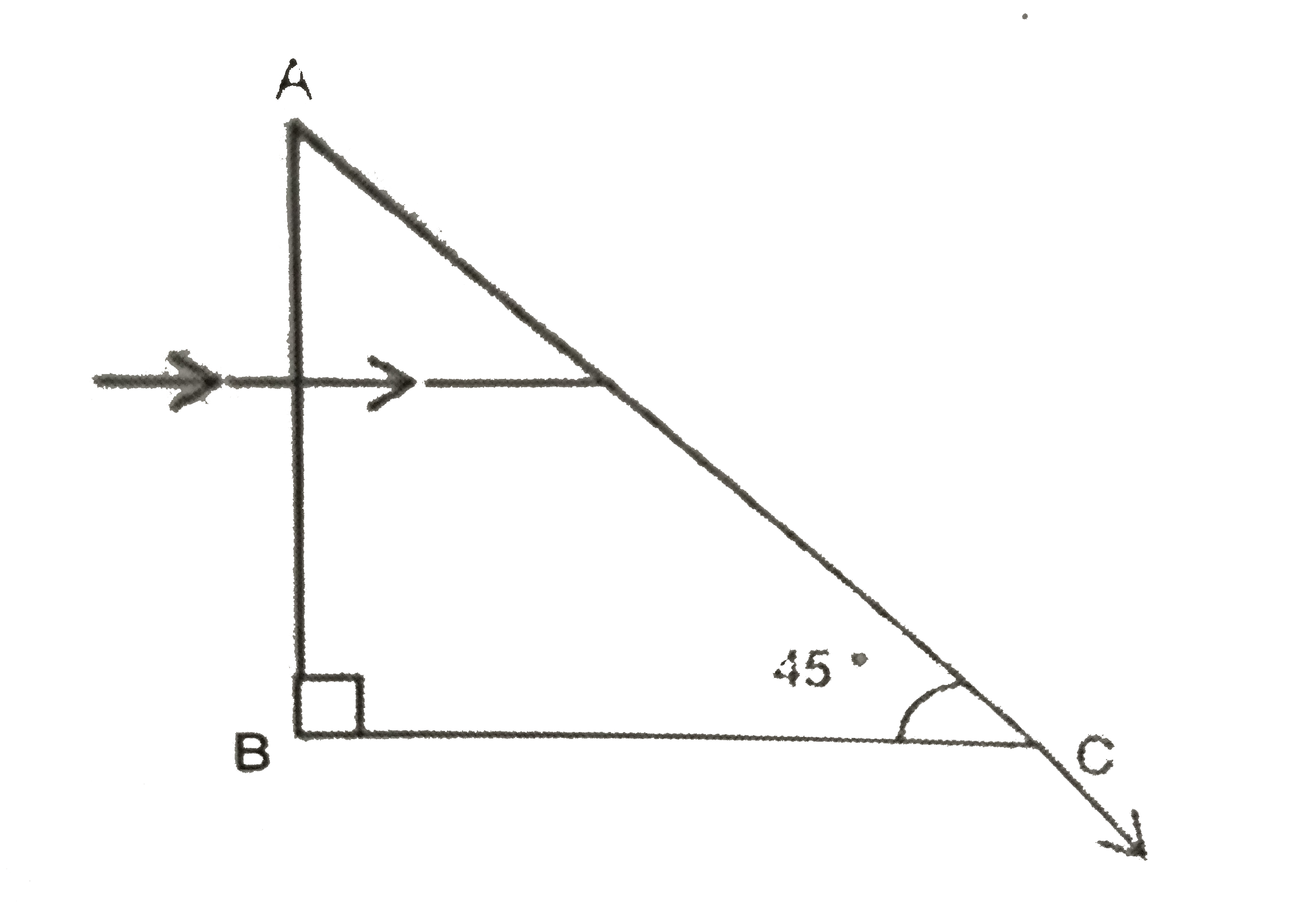
What is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
View SolutionThe refractive index of the material of a prism of refracting angle 45∘ is 1.6 for a certain monochromatic ray. What will be the minimum angle of incidence of this ray on the prism so that no TIR takes place as the ray comes out of the prism.
View Solution
Knowledge Check
The refractive index of material of a prism of angles 45∘, −45∘, and −90∘ is 1.5. The path of the ray of light incident normally on the gypotenuse side shown in
A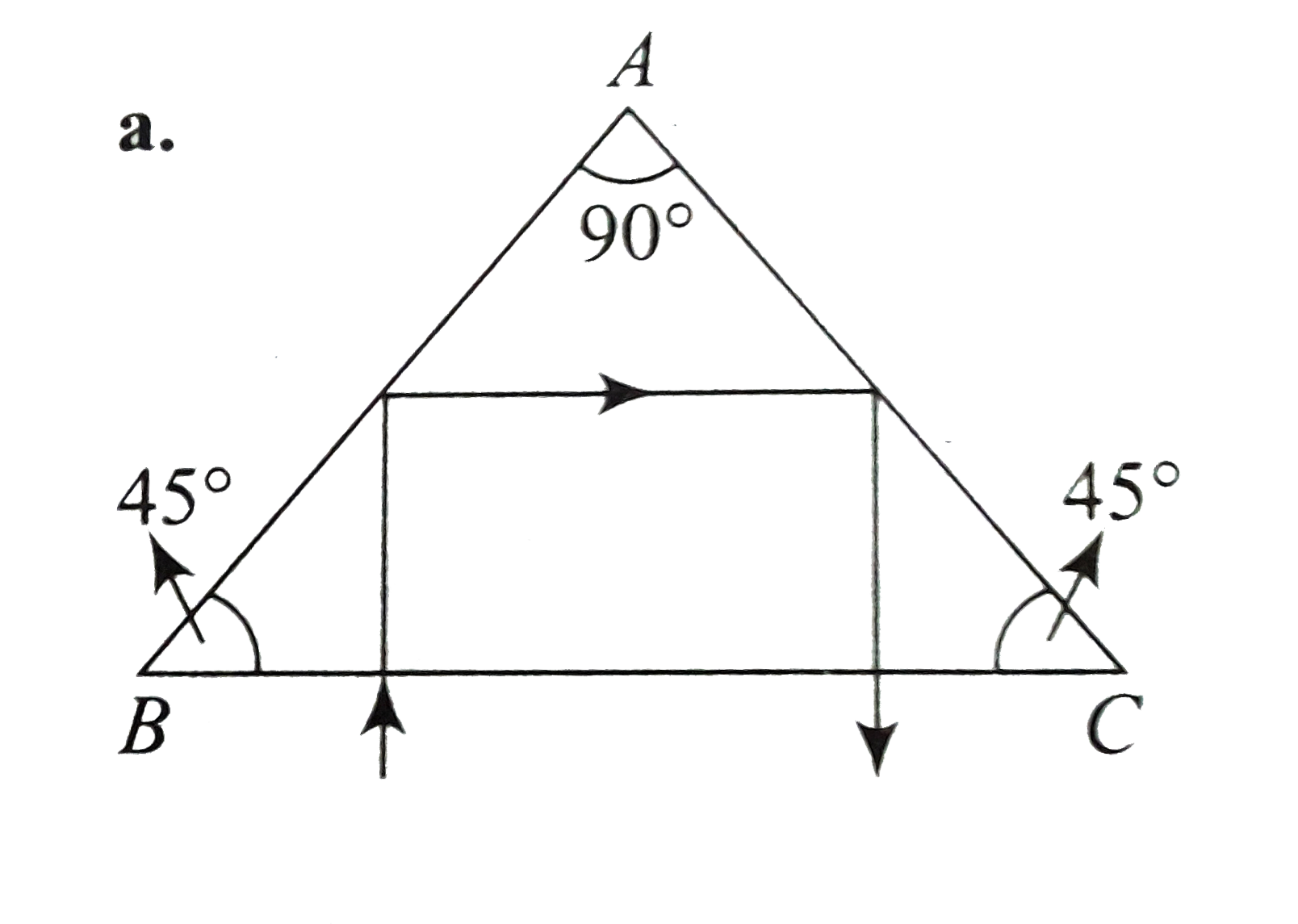 B
B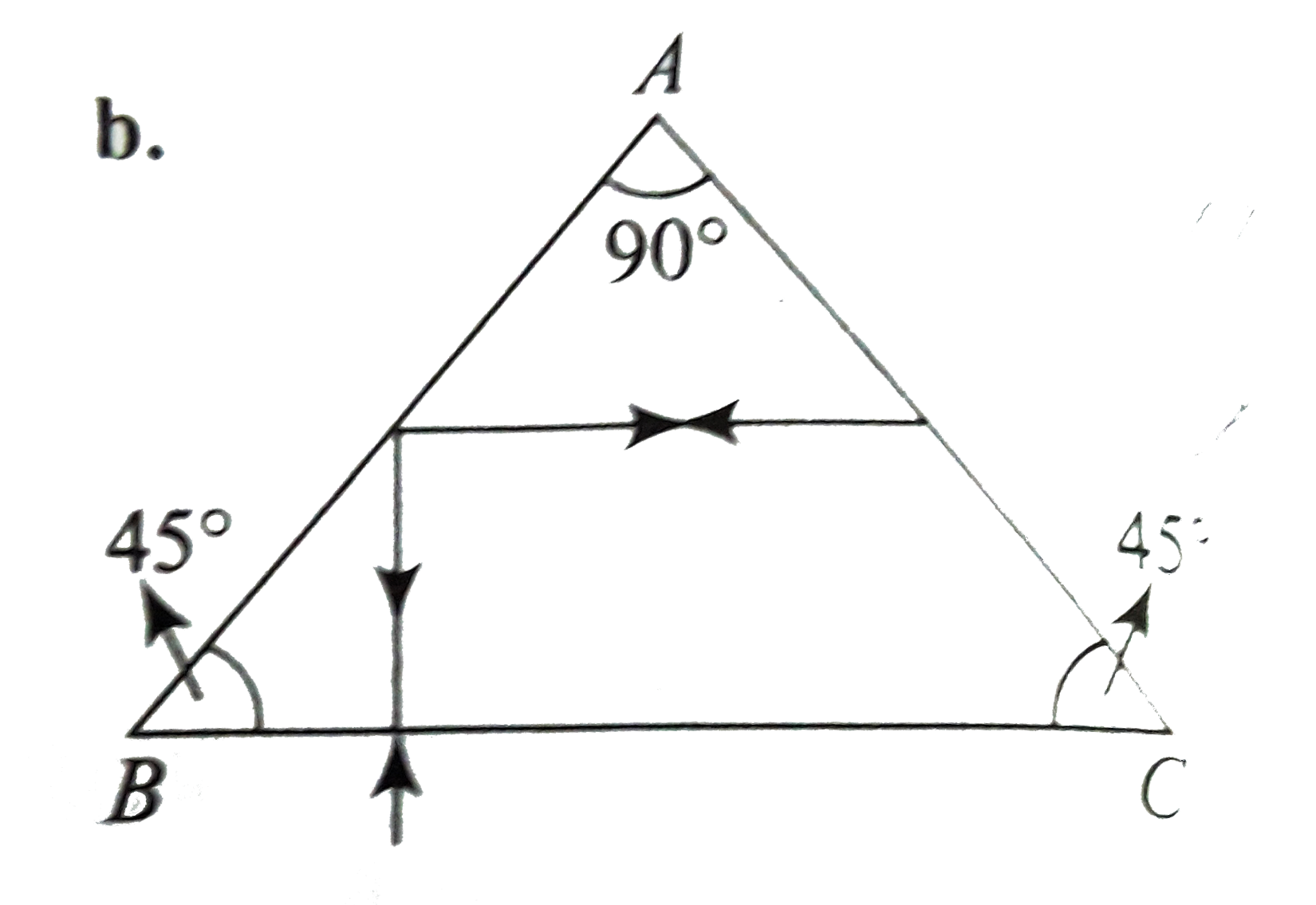 C
C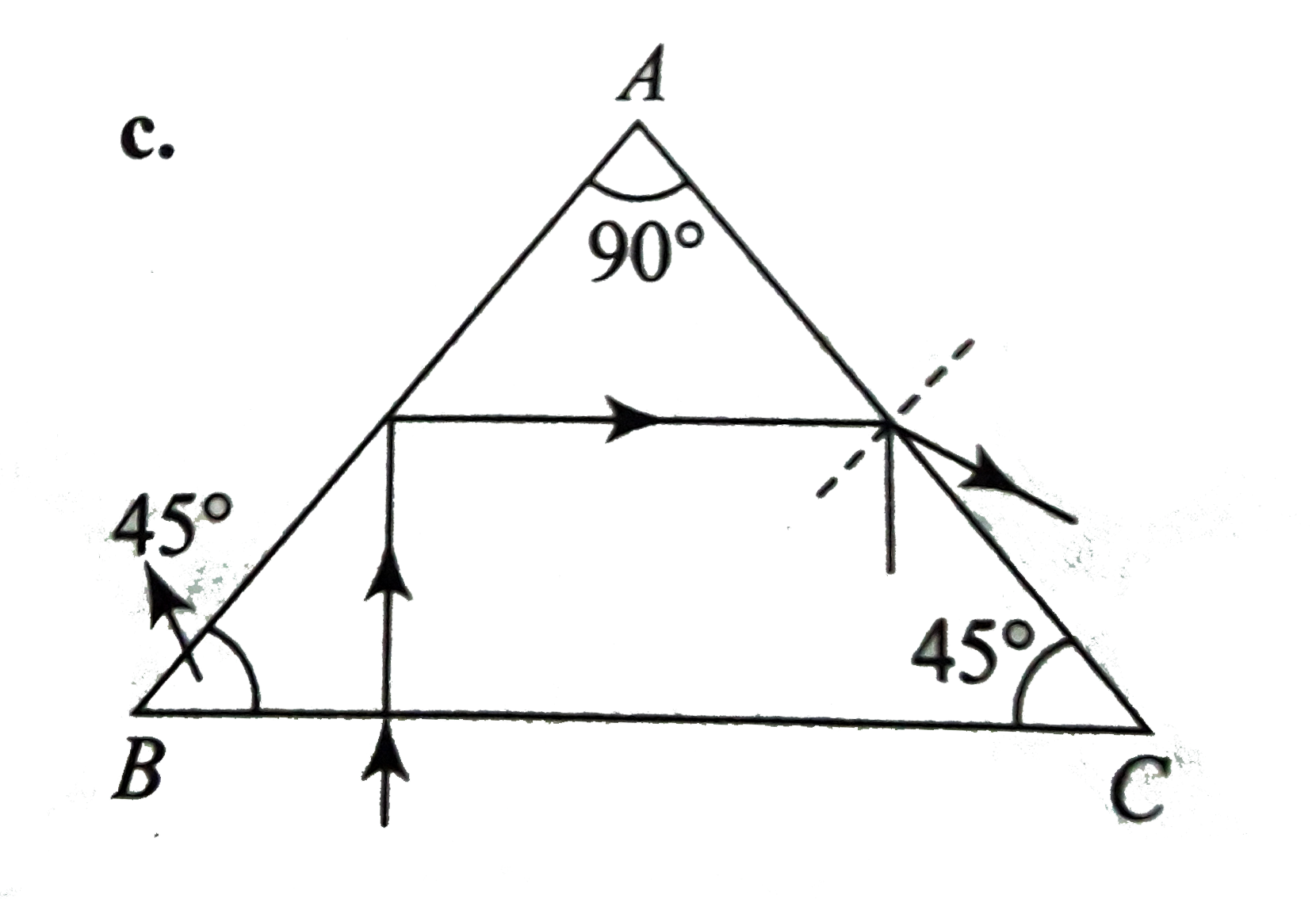 D
D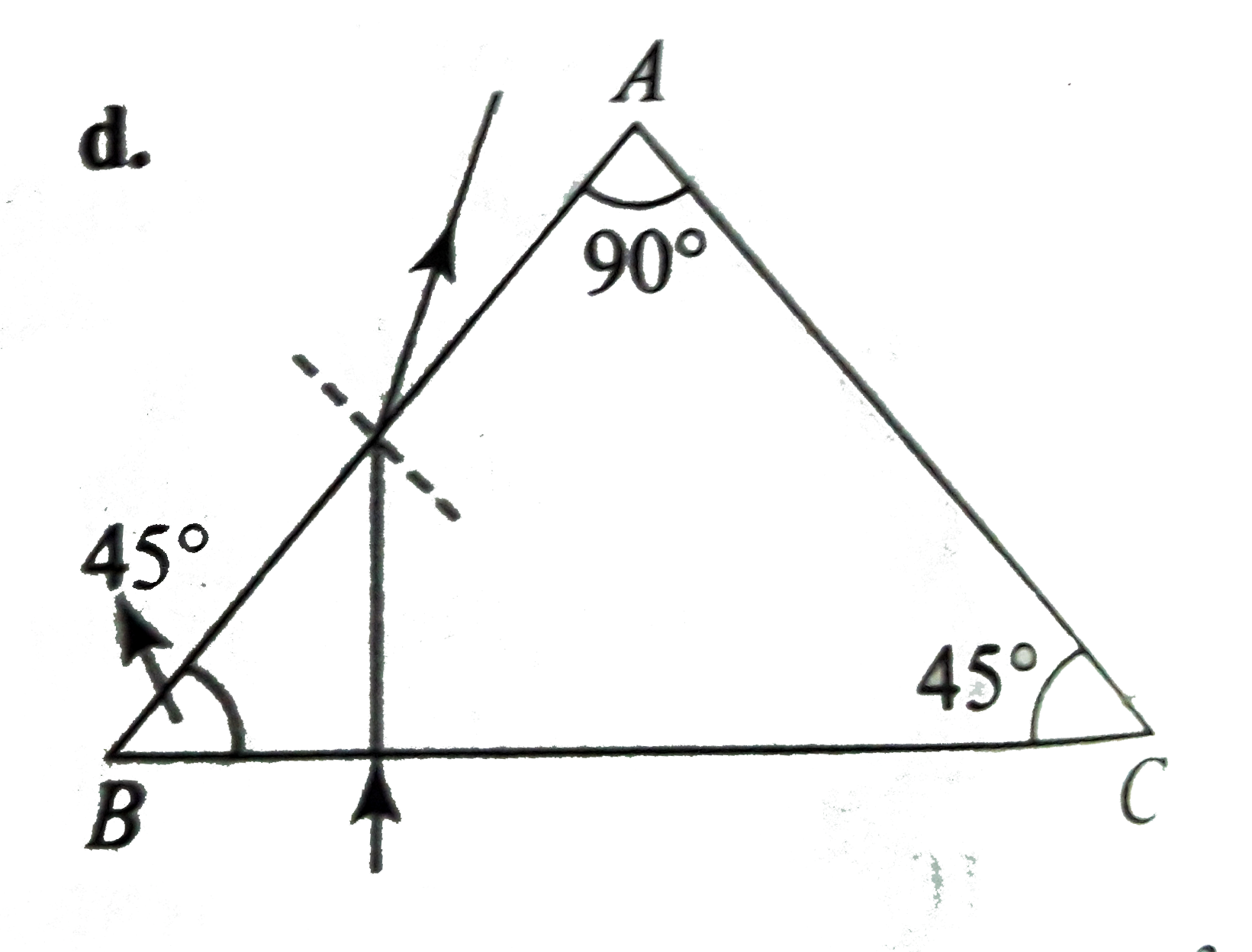
One of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
A√2B√3C3/2D2A ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
Asin−1(Iμ)Btan−1(1μ)Csin−1(μ−1μ)Dcos−1(1μ)
(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
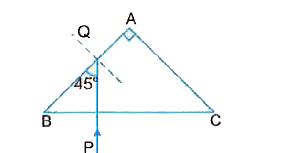
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
View SolutionA prism having a refracting angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown. A horizontal ray of light is incident on the prism. What is the angle of incidence at the mirror ?
View SolutionA ray of light is incident on a medium of refractive index √2 at an angle of incidence of 45∘. The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
View SolutionOne of the refracting surfaces of a prism of angle 30∘ is silvered. A ray of light incident at angle of 60∘ retraces its path. The refractive index of the material of prism is
View SolutionP is small angled prism of angle 3∘ made of a material of refractive index 1.5. A ray of light is incident normally to the mirror as shown in figure. M is a plane mirror. The angle of deviation for the ray reflected from the mirror M with respect to the incident ray is :

View Solution
