A closely wound coil of 100 turns and area of cross-section 1cm3 has a coefficient of self-induction 1mH. The magnetic induction in the centre of the core of the coil when a current of 2A flows in it, will be
0.022Wbm−2
0.4Wbm−2
0.8WbM−2
1Wbm−2
The correct Answer is:A
To find the magnetic induction in the center of a closely wound coil when a current flows through it, we can follow these steps:
1. Identify Given Values:
- Number of turns (N) = 100 turns
- Area of cross-section (A) = 1 cm² = 1×10−4m2
- Coefficient of self-induction (L) = 1 mH = 1×10−3H
- Current (I) = 2 A
2. Calculate the Radius of the Coil:
- The area of a circle is given by the formula:
A=πr2
- Rearranging for radius (r):
r=√Aπ=√1×10−4π≈√3.183×10−5≈5.64×10−3m
3. Use the Formula for Magnetic Field (B) at the Center of the Coil:
- The formula for the magnetic field at the center of a coil is:
B=μ0NI2r
- Where μ0 (permeability of free space) is approximately 4π×10−7T m/A.
4. Substitute the Values into the Formula:
- Plugging in the values:
B=(4π×10−7)×100×22×(5.64×10−3)
5. Simplify the Expression:
- The 2 in the numerator and denominator cancels out:
B=(4π×10−7)×100(5.64×10−3)
- Calculate:
B≈(4×3.14×10−7×100)(5.64×10−3)
B≈1.256×10−55.64×10−3≈0.00223T
6. Final Result:
- The magnetic induction (B) in the center of the coil when a current of 2 A flows through it is approximately:
B≈0.00223T or 2.23mT
- Number of turns (N) = 100 turns
- Area of cross-section (A) = 1 cm² = 1×10−4m2
- Coefficient of self-induction (L) = 1 mH = 1×10−3H
- Current (I) = 2 A
- The area of a circle is given by the formula:
A=πr2
- Rearranging for radius (r):
r=√Aπ=√1×10−4π≈√3.183×10−5≈5.64×10−3m
- The formula for the magnetic field at the center of a coil is:
B=μ0NI2r
- Where μ0 (permeability of free space) is approximately 4π×10−7T m/A.
- Plugging in the values:
B=(4π×10−7)×100×22×(5.64×10−3)
- The 2 in the numerator and denominator cancels out:
B=(4π×10−7)×100(5.64×10−3)
- Calculate:
B≈(4×3.14×10−7×100)(5.64×10−3)
B≈1.256×10−55.64×10−3≈0.00223T
- The magnetic induction (B) in the center of the coil when a current of 2 A flows through it is approximately:
B≈0.00223T or 2.23mT
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Inductor Circuits
31 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Applications Of Emi
58 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A very long straight solenoid has a cross section radius R. A number of turns per unit length is equal to n. Find the magnetic induction at the centre of the coil when a current I flows thougth it.
View SolutionThe moving coil of a galvanometer 4 cm long and 1.5 cm wide, made of 200 turns of thin wire, works in a magnetic field with induction of 0.1 T. The plane of the coil is parallel to lines of induction. Find the torque acting on the coil when a current of 1 mA flows in it.
View Solution
Knowledge Check
A closlly wound coil of 1000 turns and cross sectional area 2×10−4m2 carries a current of 1.0 A.The magnetic moment of the coil is
A0.1Am2B0.2AM2C0.4Am2D0.6Am2A rectangular coil of 20 turns and area of cross-section 25cm2 has a resistance of 100ohm. If a magnetic field which is perpendicular to the plane of the coil changes at the rate of 1000 tesla per second, the current in the coil is
A1.0 ampereB50 ampereC0.5 ampereD5.0 ampereA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
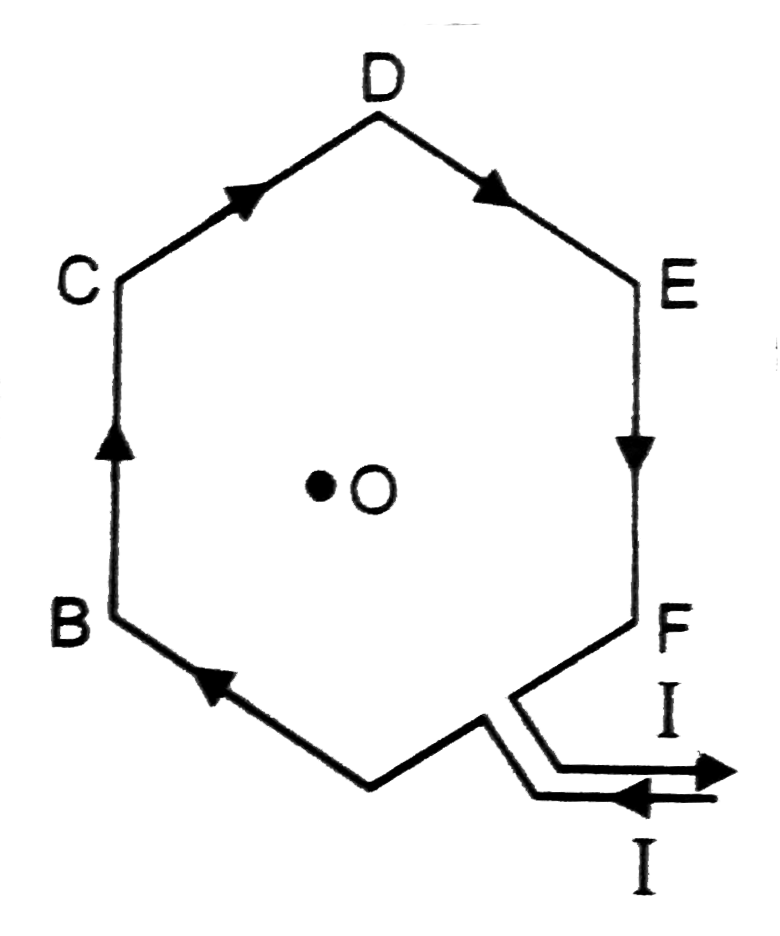 Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πa
Aμ0I3√3πaB√3μ0IπaC3√3μ0IπaDμ0I√3πa
A current I is flowing in an octagonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
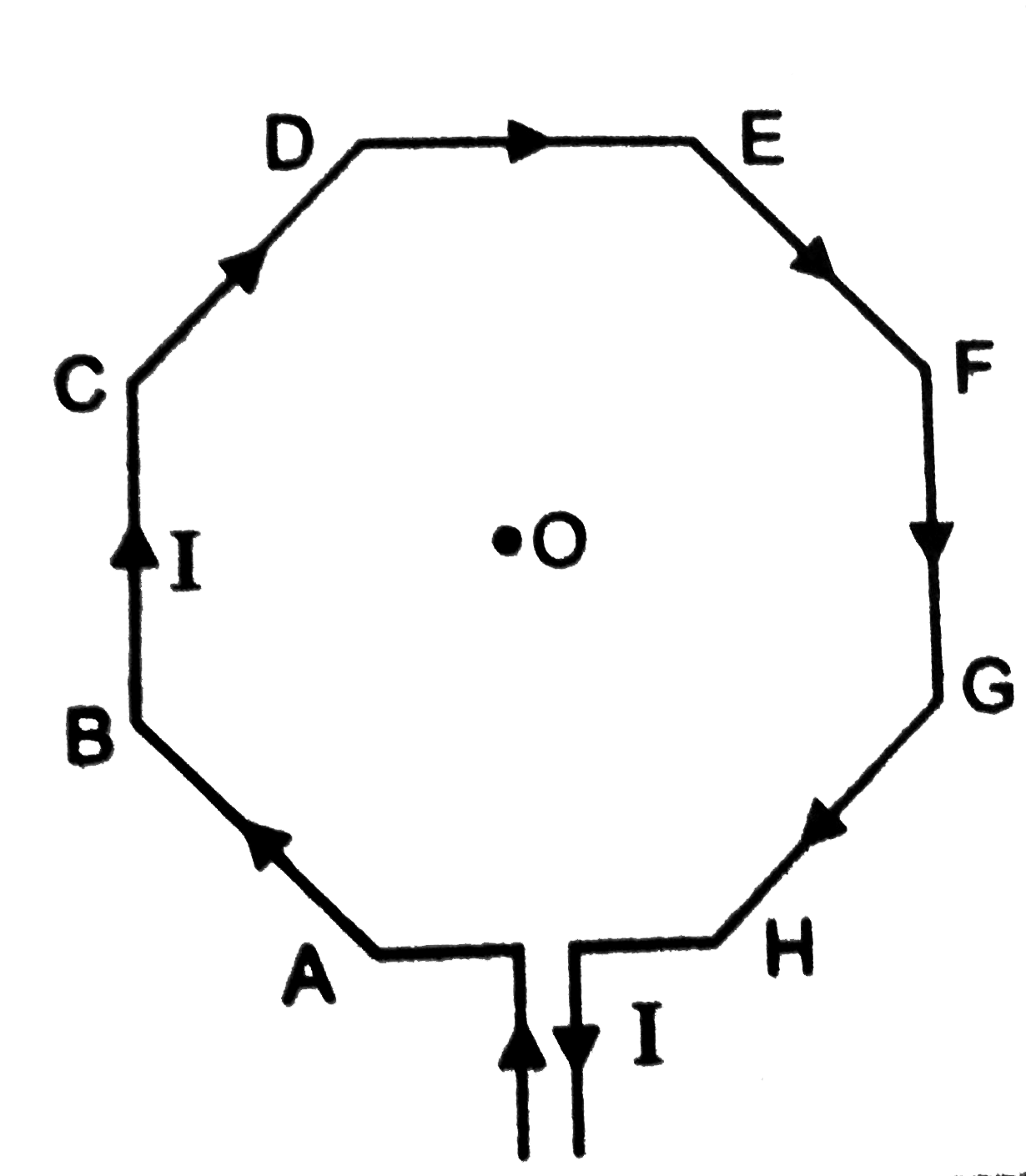
View SolutionAn air core solenoid has 1000turns and is one metre long. Its cross-sectional area is 10cm2. Its self-inductance is
View SolutionA coil of self inductance 80 mH carries a current of 2A. What is the energy stored in the coil?
View SolutionA rectangular coil of 20 turns and area of cross - section 25 sq. cm has a resistance of 100Ω. If a magnetic field which is perpendicular to the plane of coil changes at a rate of 1000 tesla per second, the current in the coil is
View SolutionA current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be

View Solution
