An $(α)$ -particle and a proton are both simultaneously projected in opposite direction into a region of constant magnetic field perpendicular to the direction of the field. After some time it is found that the velocity of the $(α)$ -particle has changed in a direction by $45^{\circ}$ . Then at this time, the angle between velocity vectors of $(α)$ -particle and proton is

A

$90^{\circ}$

B

$45^{\circ}$

C

$135^{\circ}$

D

none

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$ω = q B / m, ω_{p} = e B / m, ω_{α} = \frac{2 e B}{4 m} = 2 ω_{p}$

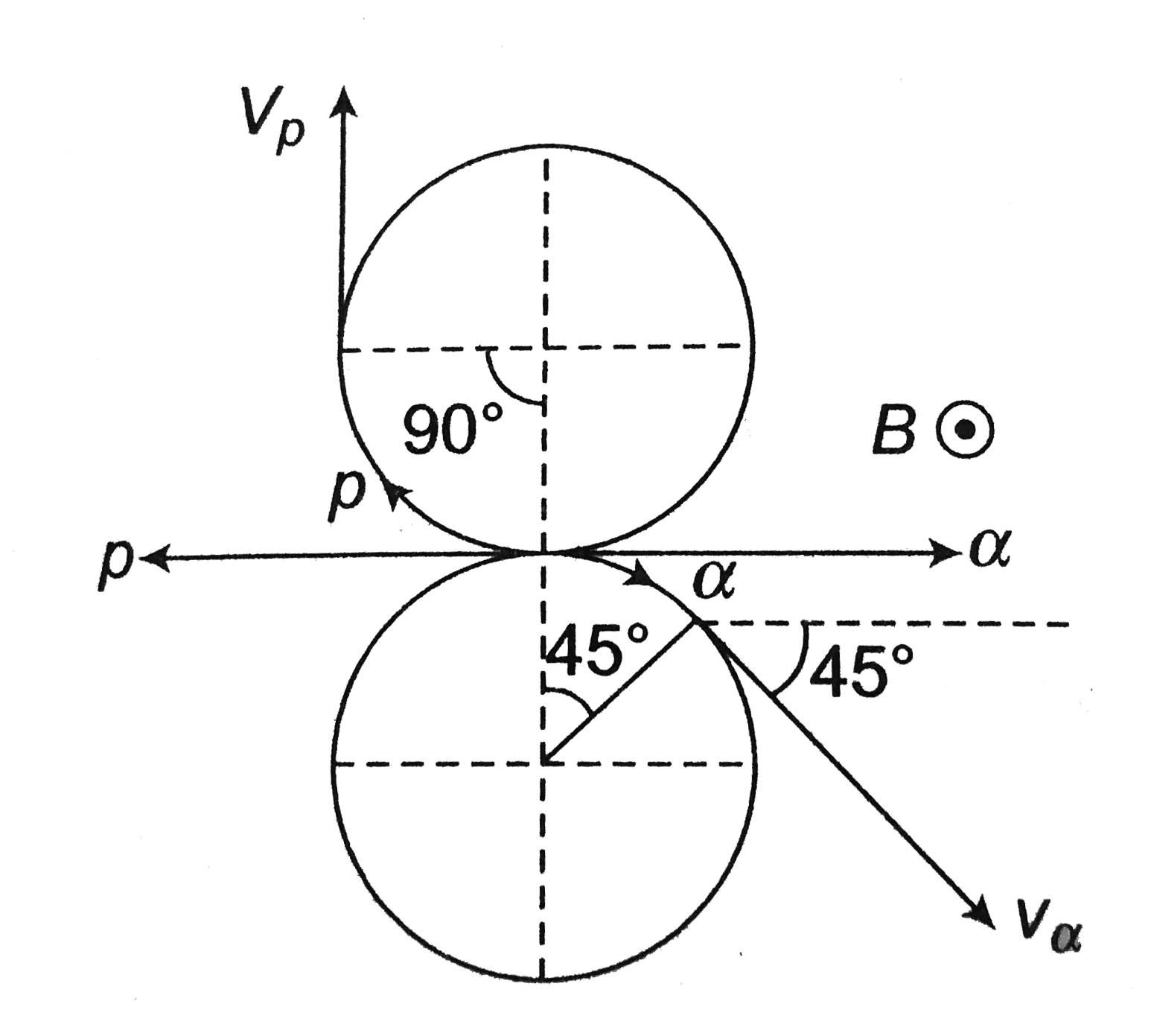
So proton will cover double angle in same time a that of $α$ -particle. Clearly from figure angle between $v_{α}$ and $v_{p}$ is $135^{\circ}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An $α$ particle and a proton travel with same velocity in a magnetic field perpendicular to the direction of their veloccites find the ratio of the radii of their circular path
A $4 : 1$
B $1 : 4$
C $2 : 1$
D $1 : 2$
Question 2 - Select One
A proton and an electron are projected into a region of uniform magnetic field in a direction perpendicular to the field. If they have the same initial velocities then
AThey move in circular paths of same radii
BThey experience equal force
CThe trajectory of the electron is more curved
DTheir velocity remain equal to each other through out the motion
Question 3 - Select One
An alpha particle and a proton travel with same velocity in a magnetic field perpendicular to the direction of their velocities. The ratio of the radii of their circular paths is
A $4 : 1$
B $1 : 4$
C $2 : 1$
D $1 : 2$

A2Z-SOURCE AND EFFECT OF MAGNETIC FIELD-Section D - Chapter End Test

Home
Ask Doubt
Profile