A uniform magnetic field B and a uniform electric field E act in a common region. An electron is entering this region of space. The correct arrangement for it to escape undeviated is
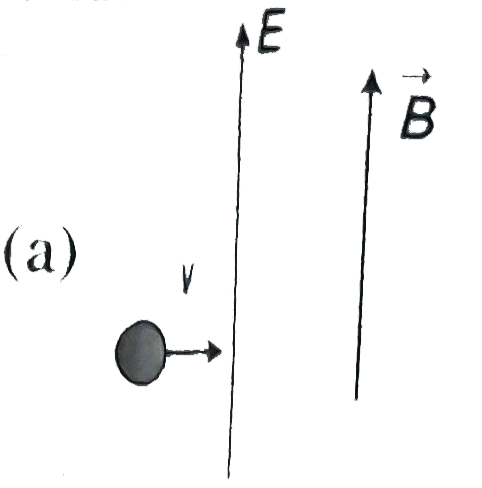

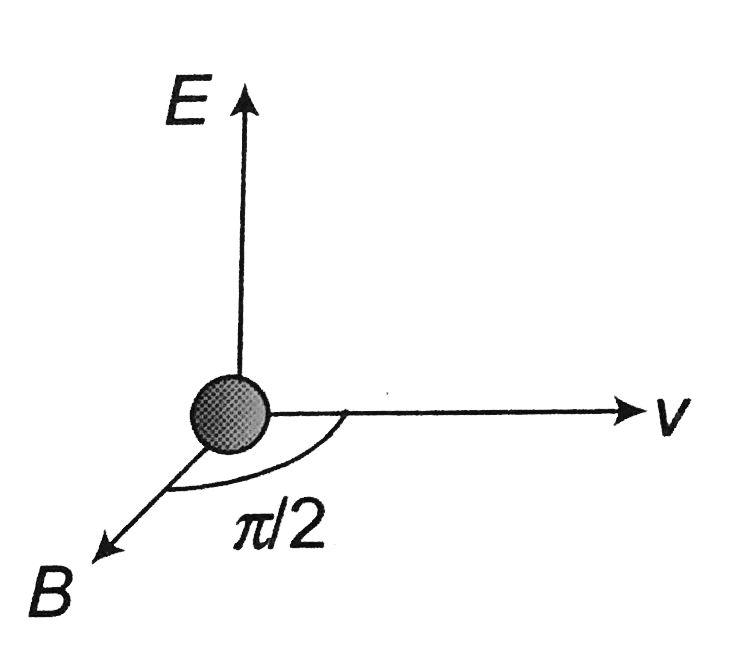

The correct Answer is:C
To determine the correct arrangement for an electron to escape undeviated in the presence of uniform electric and magnetic fields, we can follow these steps:
1. Understand the Forces Acting on the Electron:
- The force due to the electric field E acting on the electron is given by:
FE=Q⋅E
- The force due to the magnetic field B acting on the electron when it is moving with velocity v is given by:
FB=Q⋅(v×B)
- Here, Q is the charge of the electron (which is negative).
2. Condition for Undeviated Motion:
- For the electron to move undeviated, the net force acting on it must be zero. This means that the electric force must be equal in magnitude and opposite in direction to the magnetic force:
FE+FB=0⇒FE=−FB
3. Direction of Forces:
- The electric force FE acts in the direction of the electric field E.
- The magnetic force FB acts in the direction given by the right-hand rule (for a positive charge), but since we are dealing with an electron (negative charge), the direction of FB will be opposite to that predicted by the right-hand rule.
4. Analyzing Each Arrangement:
- Option A: If E is in one direction and B is perpendicular to it, the forces will not cancel. Hence, this option is not valid.
- Option B: Similar analysis shows that the forces will not balance. Hence, this option is not valid.
- Option C: If the electric field E is in one direction and the magnetic field B is perpendicular to it, the forces can balance if they are in opposite directions. This option is valid.
- Option D: The forces will not cancel out as they are not in opposite directions. Hence, this option is not valid.
5. Conclusion:
- The only arrangement that allows the electron to escape undeviated is Option C.
Final Answer:
The correct arrangement for the electron to escape undeviated is Option C.
- The force due to the electric field E acting on the electron is given by:
FE=Q⋅E
- The force due to the magnetic field B acting on the electron when it is moving with velocity v is given by:
FB=Q⋅(v×B)
- Here, Q is the charge of the electron (which is negative).
- For the electron to move undeviated, the net force acting on it must be zero. This means that the electric force must be equal in magnitude and opposite in direction to the magnetic force:
FE+FB=0⇒FE=−FB
- The electric force FE acts in the direction of the electric field E.
- The magnetic force FB acts in the direction given by the right-hand rule (for a positive charge), but since we are dealing with an electron (negative charge), the direction of FB will be opposite to that predicted by the right-hand rule.
- Option A: If E is in one direction and B is perpendicular to it, the forces will not cancel. Hence, this option is not valid.
- Option B: Similar analysis shows that the forces will not balance. Hence, this option is not valid.
- Option C: If the electric field E is in one direction and the magnetic field B is perpendicular to it, the forces can balance if they are in opposite directions. This option is valid.
- Option D: The forces will not cancel out as they are not in opposite directions. Hence, this option is not valid.
- The only arrangement that allows the electron to escape undeviated is Option C.
The correct arrangement for the electron to escape undeviated is Option C.
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Force On A Current Carrying Conductor In Magnetic Field
42 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Dipole
32 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
An electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity then
View Solution
Knowledge Check
A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the region such that its velocity is pointed along the direction of fields, then the electron
AWill turn towards left of direction of motionBWill turn towards right of direction of motionCSpeed will decreaseDSpeed will increaseA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the region such that its velocity is pointed along the direction of fields, then the electron
Awill turn towards right of direction of motionBspeed will decreaseCspeed will increaseDwill turn towards left of direction of motionA uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the same direction then the electron
Aspeed will increaseBwill turn towards left of direction of motionCwill turn towards right of direction of motionDspeed will decrease
A uniform electric field and a uniform magnetic field exist in a region in the same direction. An electron is projected with a velocity pointed I the same direction. Then the electron will:
View SolutionA uniform electric field and a uniform magneitc field exist in a region in the same direction An electron is projected with velocity pointed in the same direction the electron will
View SolutionA particle moves in a region having a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field directjion. The path of the particle will be
View SolutionQuestion Stimulus :- In a certain region, a uniform magnetic field exists in the direction from south to north. An electron enters the field from east to west. The force experienced by the electron due to the field is
View SolutionAn electron traveling in a uniform electric field passes from a region of potential V1 to a region of higher potential V2. Then

View Solution
