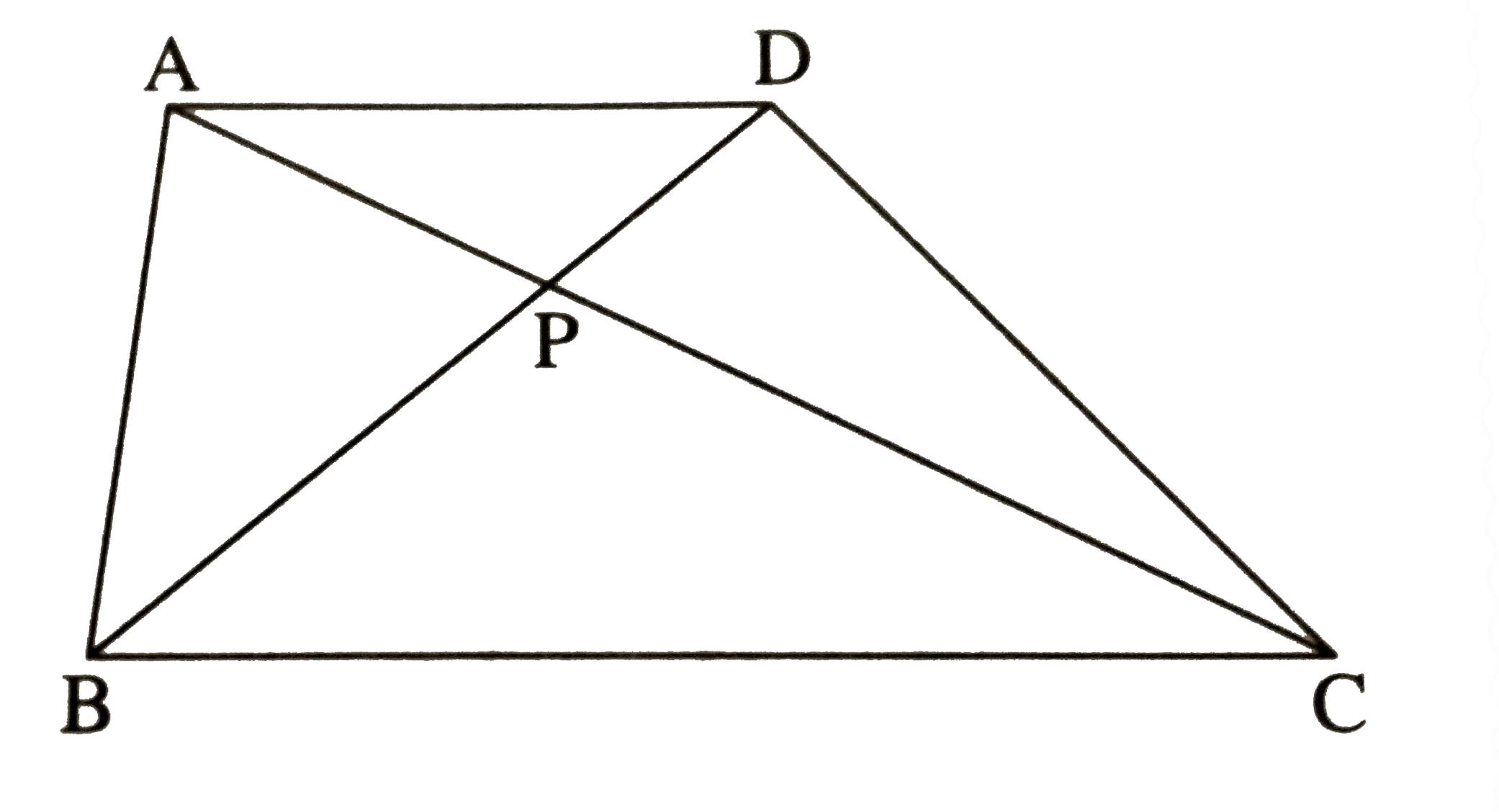
In □ABCD , side BC∣∣ side AD. Digonals AC and BD intersect each other at P. If AP=13AC then prove DP=12BP.
Step by step video & image solution for In squareABCD , side BC|| side AD. Digonals AC and BD intersect each other at P. If AP=(1)/(3)AC then prove DP=(1)/(2)BP. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Additonal Problems for Practice(Based on Practice Set 1.4)
8 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Chapter Assessment
19 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Additonal Problems for Practice(Based on Practice Set 1.2)
11 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
Knowledge Check
In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)In a quadrilateral ABCD, with unequal sides if the diagonals AC and BD intersect at right angles, then
AAB2+BC2=CD2+DA2BAB2+CD2=BC2+DA2CAB2+AD2=BC2+CD2DAB2+BC2=2(CD2+DA2)
In the figure, seg AC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View SolutionIn the figure, set aC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
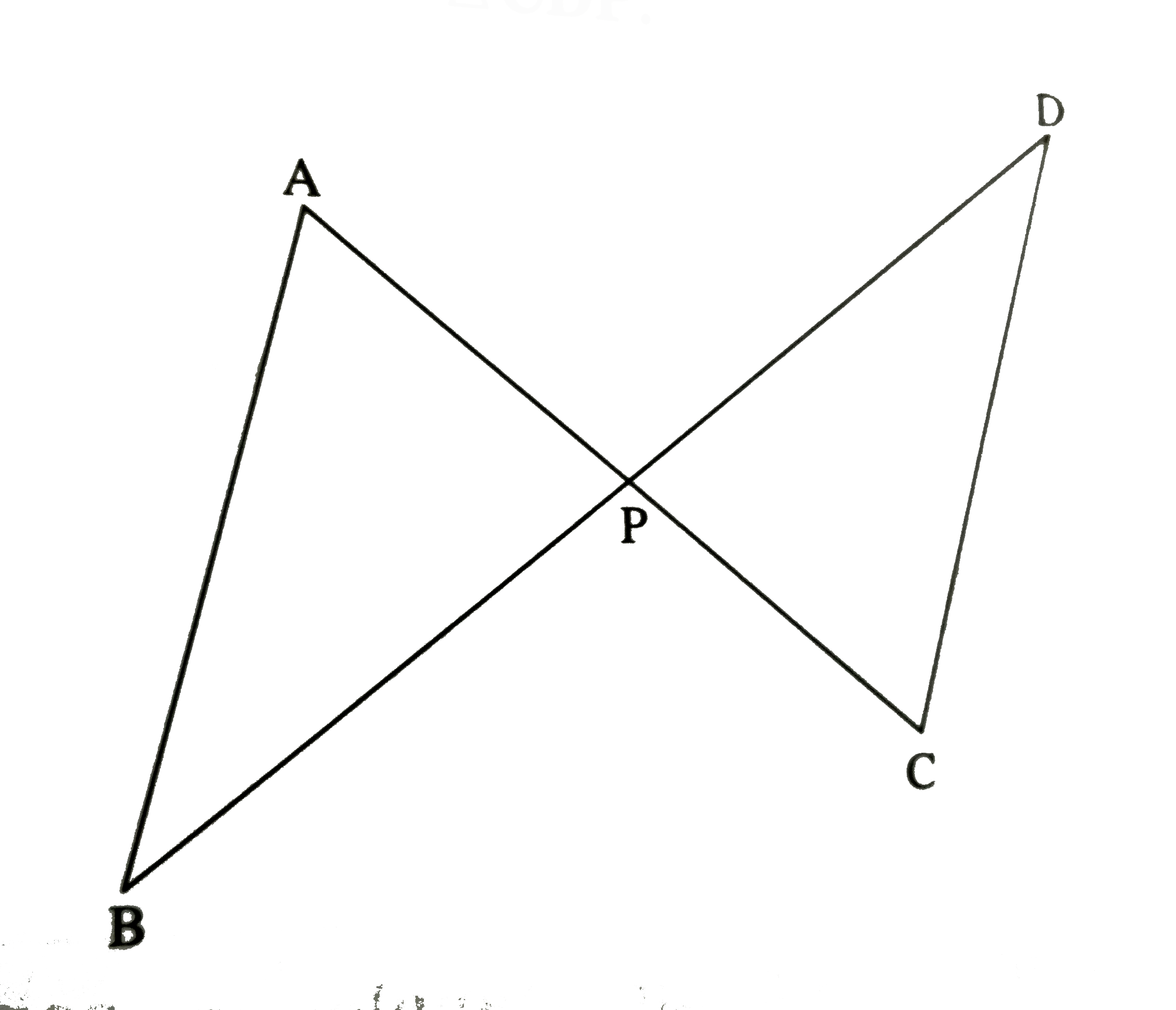
View SolutionIn a trapezium ABCD, AB is parallel to DC. The diagonals AC and BD intersect at P. If AP:PC=4:(4x−4) and BP:PD=(2x−1):(2x+4), then what is the value of x ?
View SolutionIn trapezium AC and BD intersect each other at point P. Then prove that A(ΔABP)A(ΔCPD)=AB2CD2.
View Solutionif ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solution