In the figure A−D−C and B−E−C seg DE∣∣ side AB. If AD=5,DC=3,BC=6.4 then find BE.
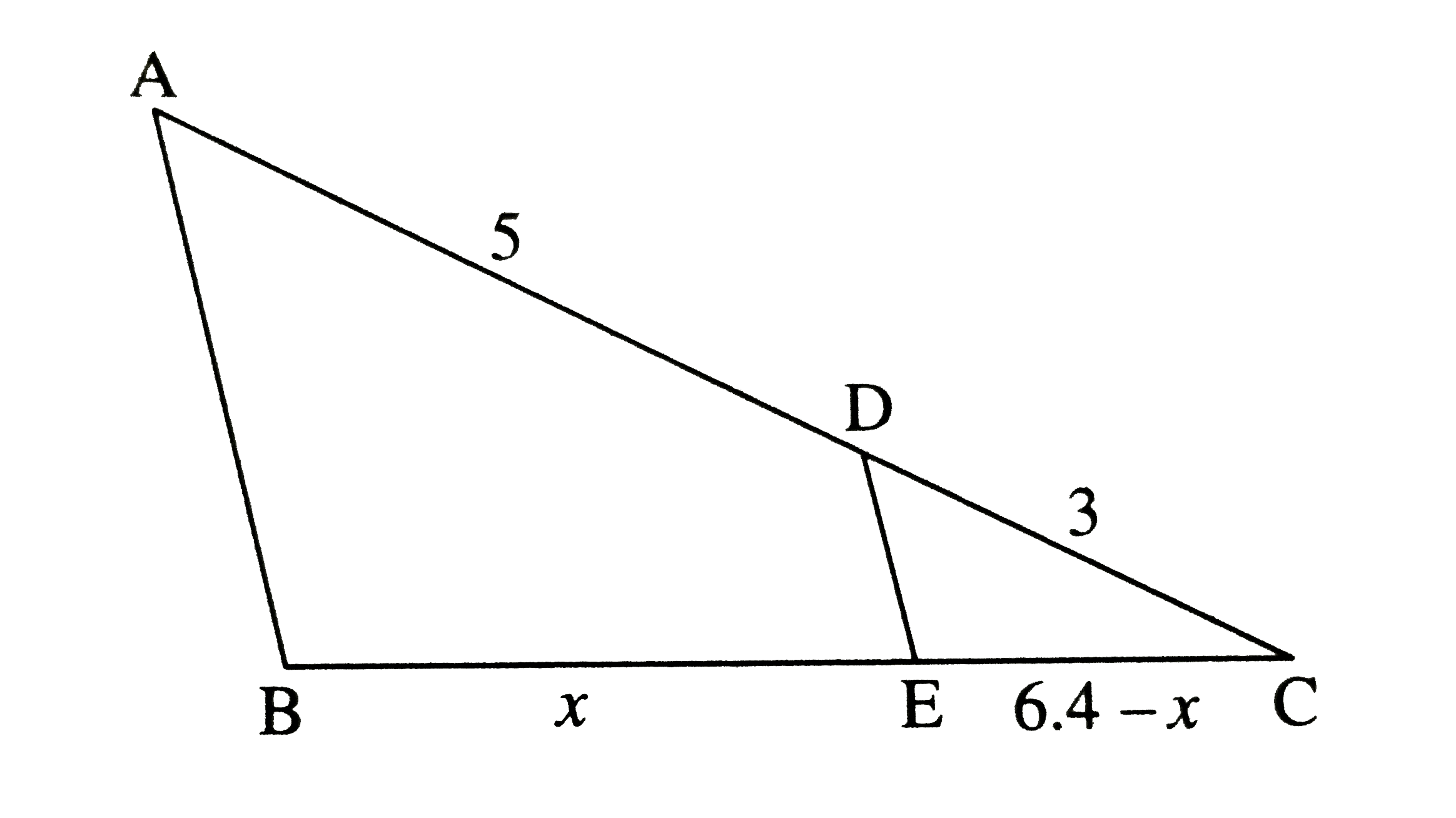
The correct Answer is:∴ x = 328=4
Step by step video solution for In the figure A-D-C and B-E-C seg DE|| side AB. If AD=5, DC=3, BC=6.4 then find BE. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Multiple Choice Questions
28 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Additonal Problems for Practice( Basid on Practice Set 1.1)
11 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Problem Set - 1
19 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
If A:B = 5: 6 and B:C = 4:7, then find A:B:C
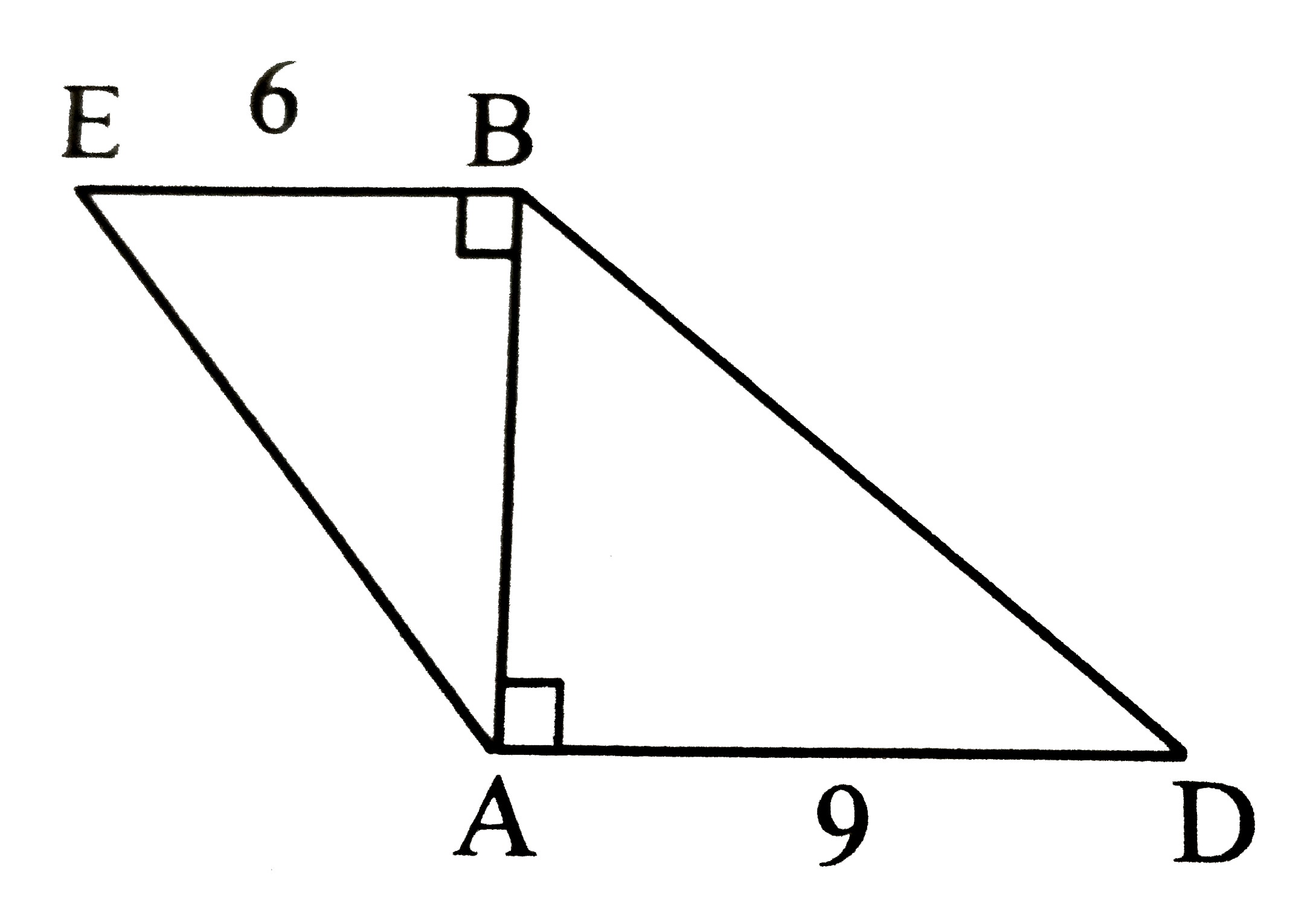
View SolutionIn the given figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and AD = 9, then find A(ΔABE)A(ΔBAD).
View SolutionIn the ΔABC, D and E are points on side AB and AC respectively such that DE II BC. If AE=2cm, AD=3cm and BD=4.5cm, then find CE.
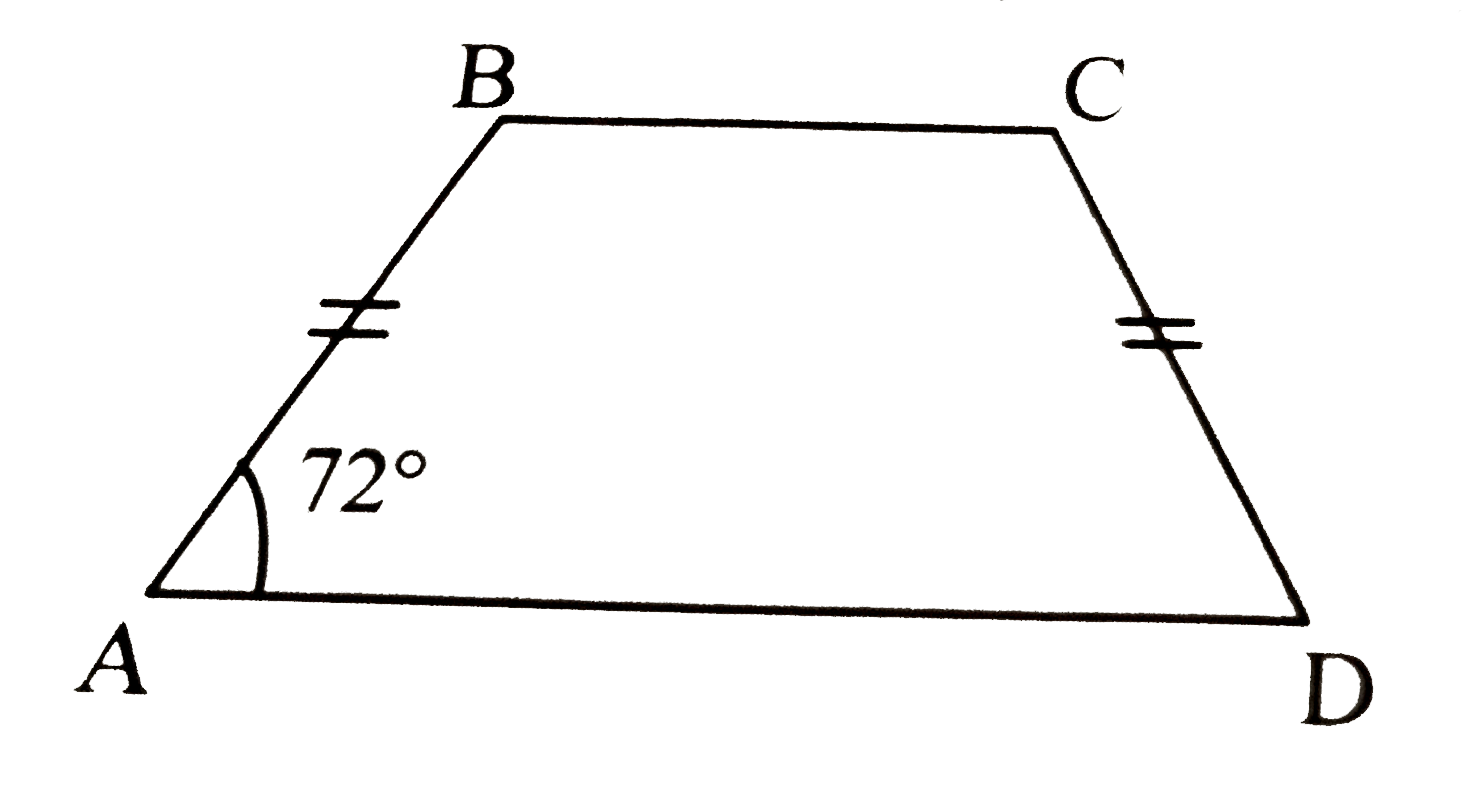
View SolutionIn trapezium ABCD, side BC ∣∣ side AD, side AB ≅ side DC. If ∠A=72∘ , then find the measures of ∠B and ∠D .
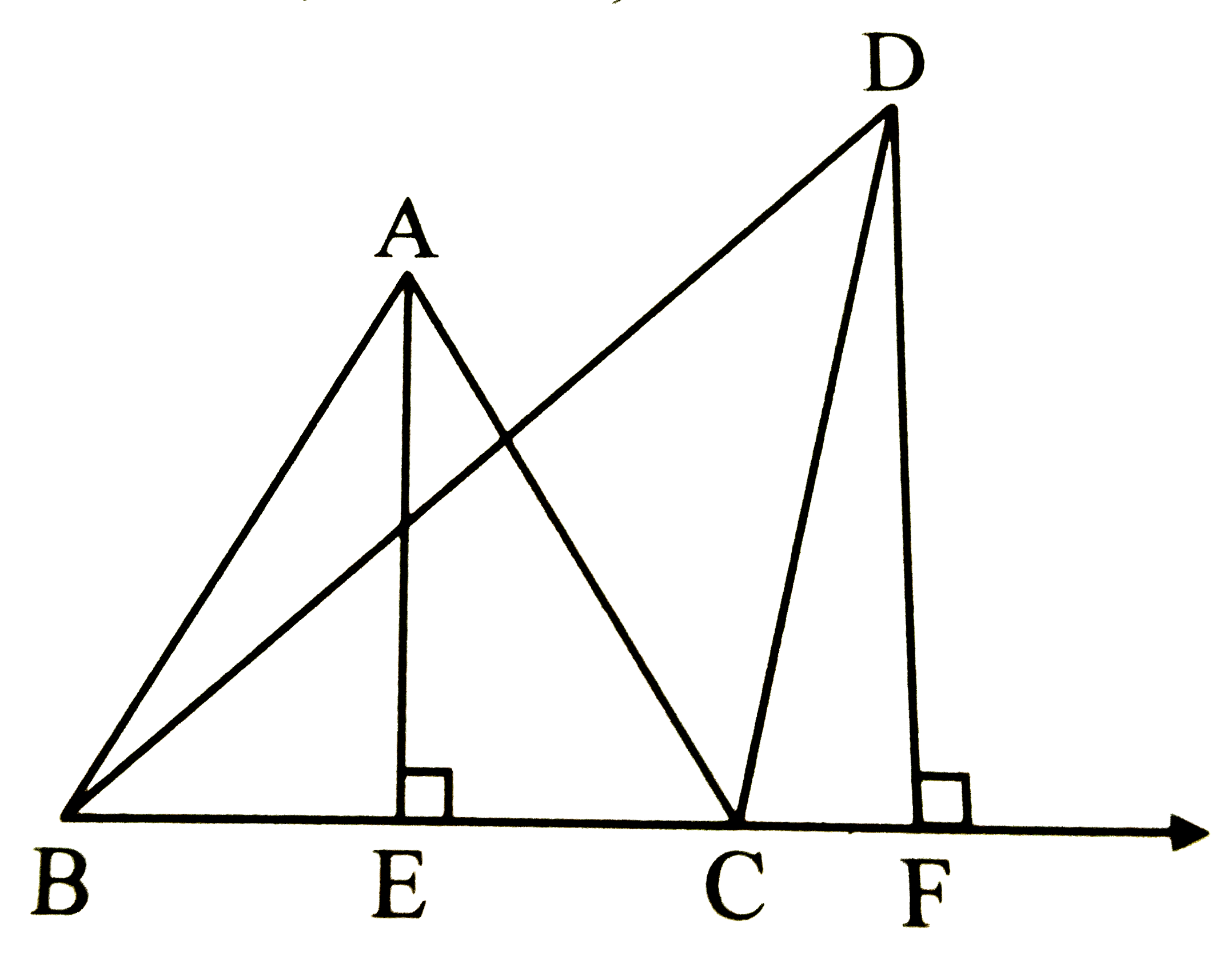
View SolutionIn given figure, seg AE ⊥ seg BC, seg DF ⊥ line BC,
AE = 4, DF = 6, then find A(ΔABC)A(ΔDBC).
View SolutionIn the following figure, seg AB⊥seg BC, seg DC⊥seg BC.
If AB = 2 and DC = 3, find A(ΔABC)A(ΔDCB).
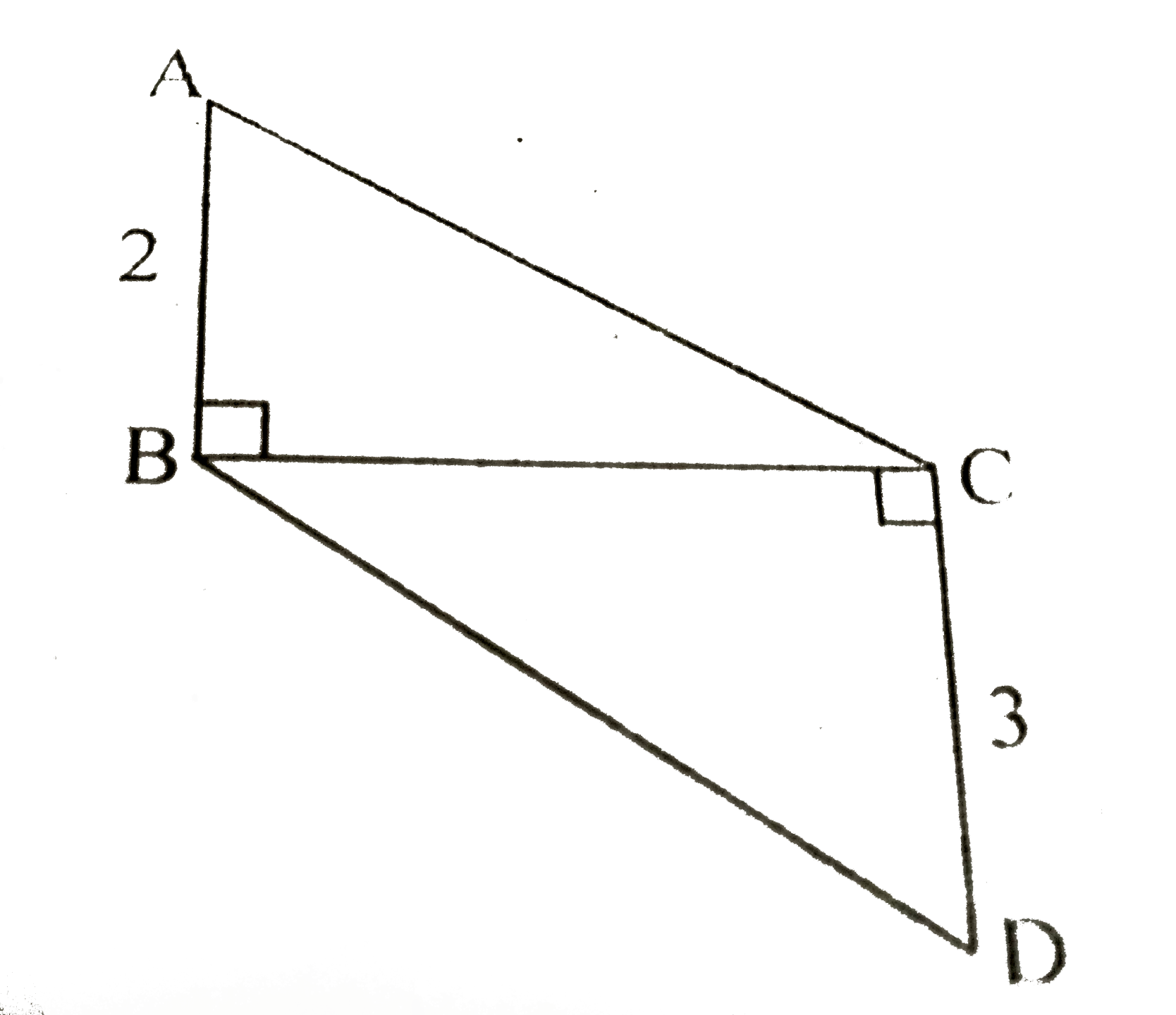
View SolutionIn the figure, seg DE∣∣ side AB. DC=2BD, A(ΔCDE)=20cm2. Find A(□ABDE).
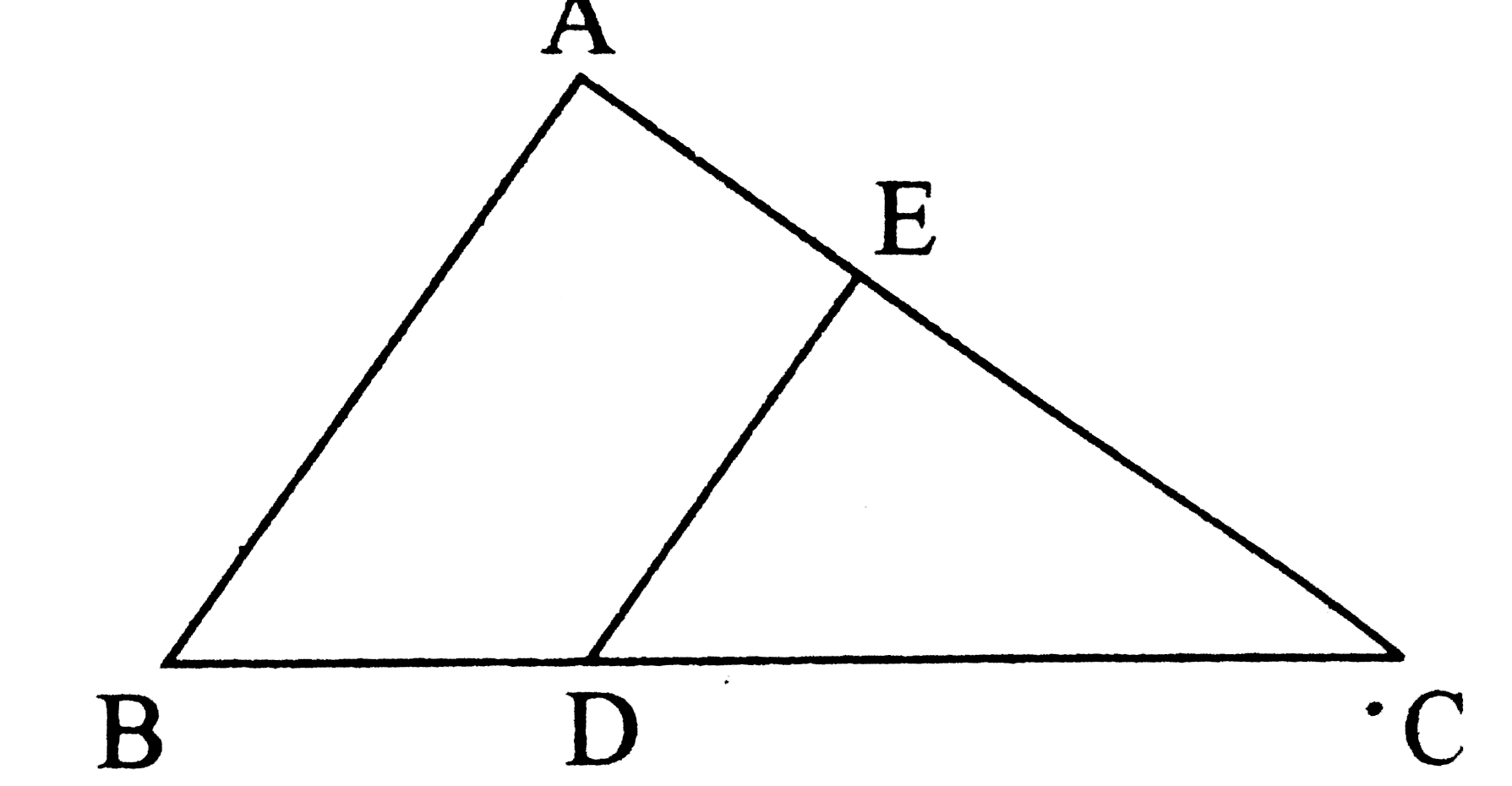
View SolutionIn the figure D is a point on BC such that ∠ABD=∠CAD. If AB=5cm,AD=4cm and AC=3cm. Find (i) BC (ii) DC (iii) A(ΔACD):AIΔBCA).
View SolutionD and E are respectively the points on the sides AB and AC of a triangle ABC such that AD=2cm, BD=3cm,BC=7.5cm and DE || BC. Then length of DE (in cm) is
(a) 2.5
(b) 3
(c) 5
(d) 6
View SolutionIn the figure, AD=17, AB=10, BC=15. ∠ABC=∠BCD=90∘ seg AE⊥ side CD then find the length of (i)AE (ii)DE (iii)DC.
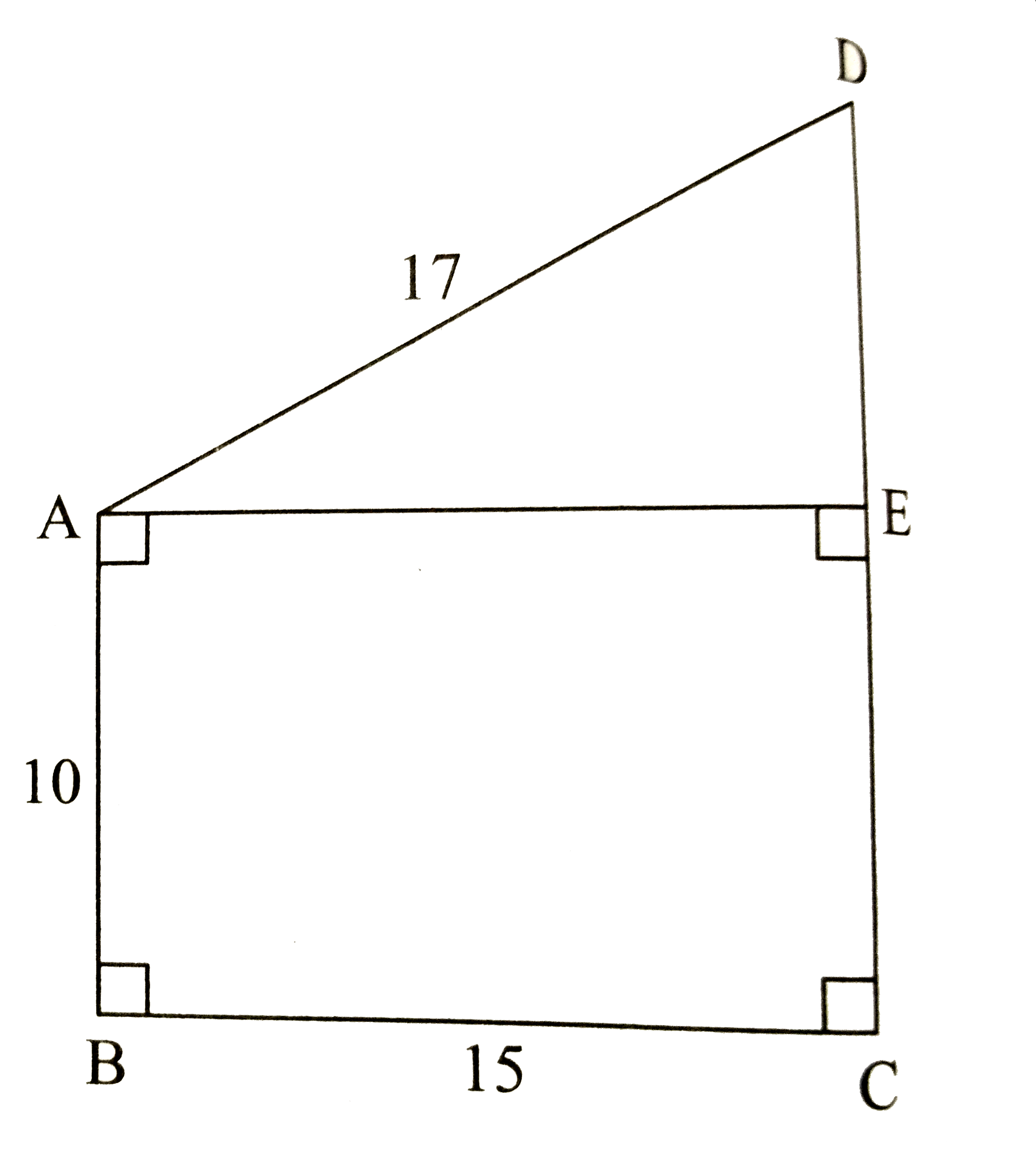
View Solution
