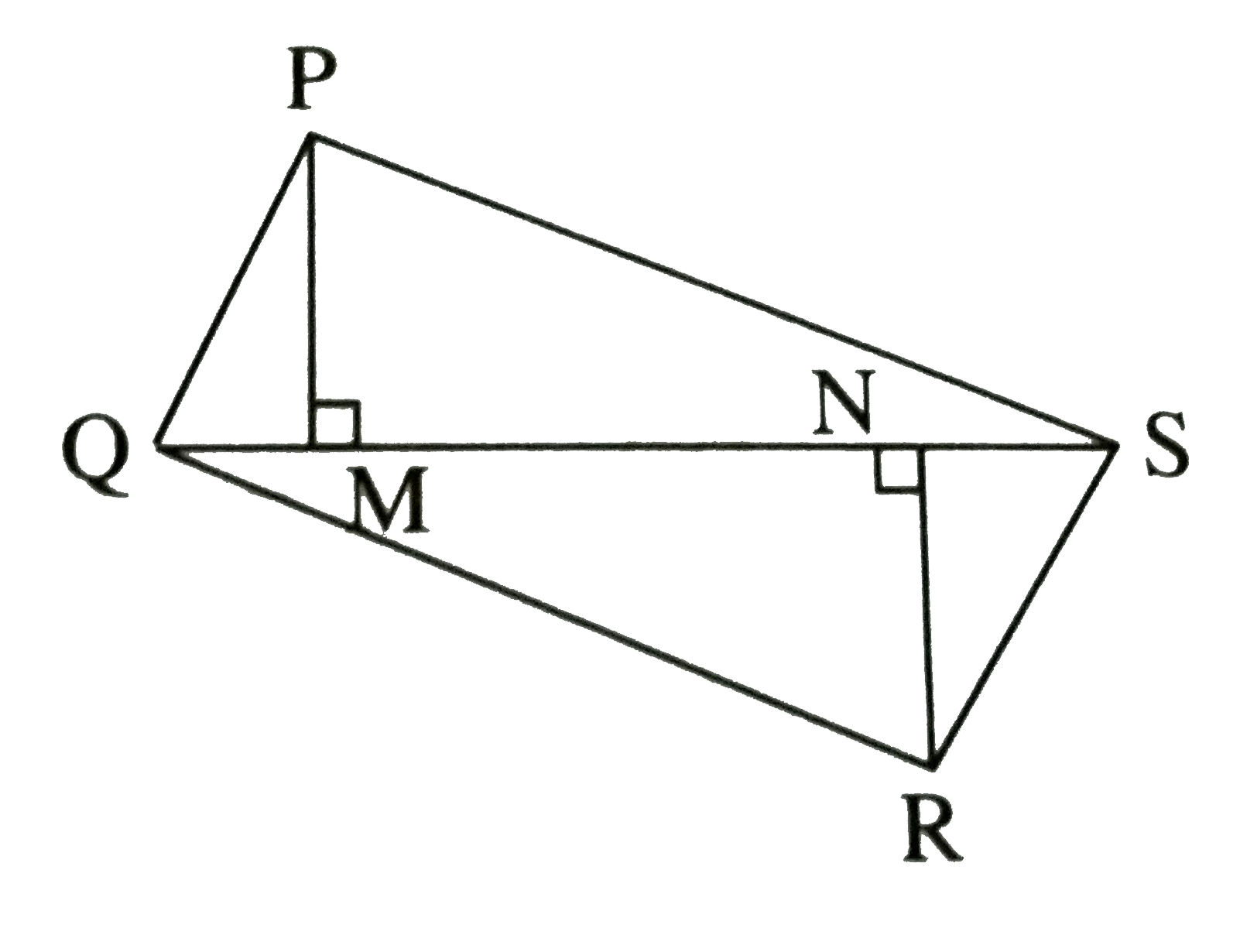
In the adjoining figure, PM = 10 cm, A(ΔPQS) = 100sq.cm,A(ΔQRS)=110sq. cm, then find NR.
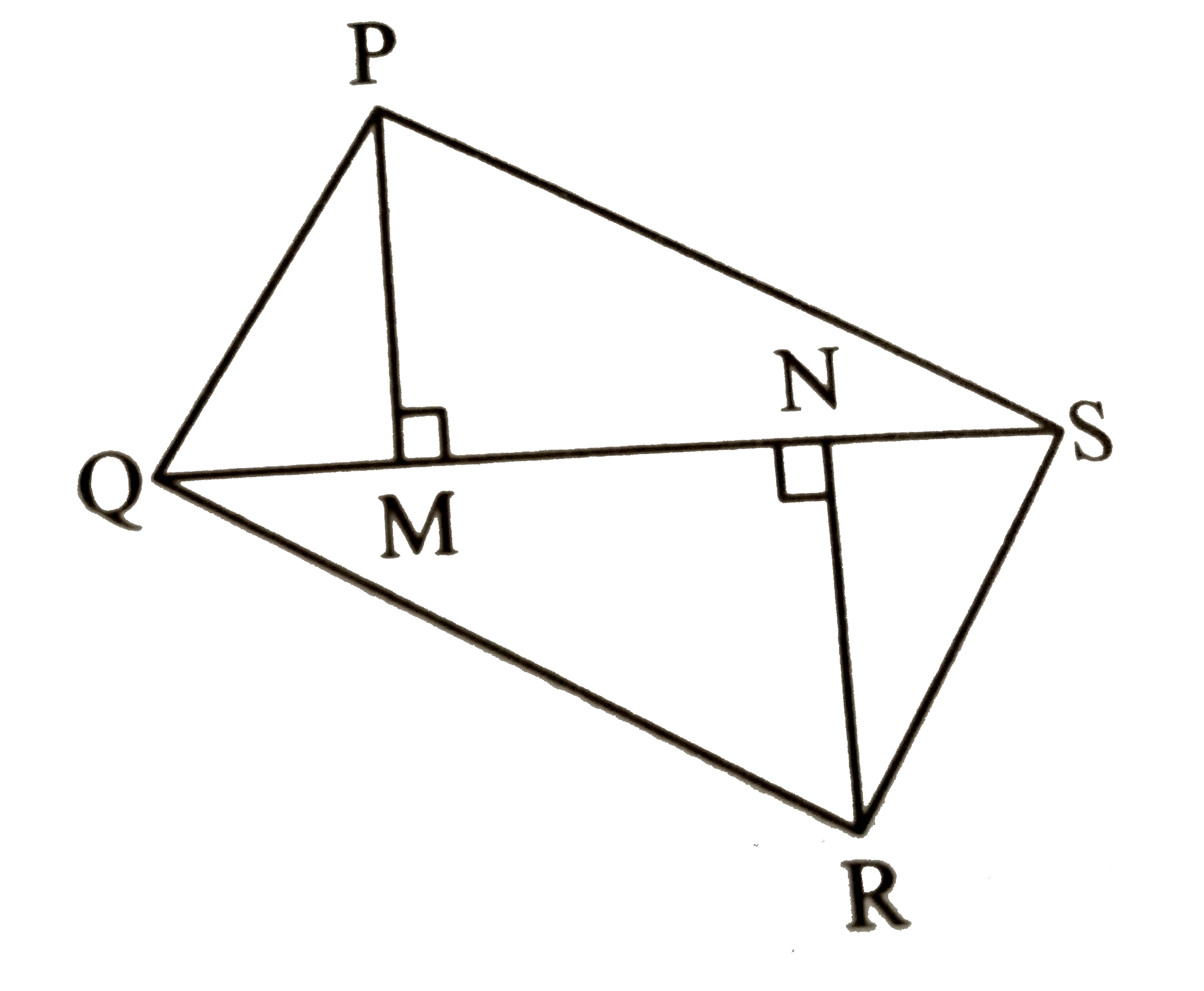
The correct Answer is:∴ NR = 11 cm
Step by step video & image solution for In the adjoining figure, PM = 10 cm, A(DeltaPQS) = 100sq. cm, A(DeltaQRS) = 110sq. cm, then find NR. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Activites for Practice
4 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Multiple Choice Questions
28 Videos
- SIMILARITY BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.4
7 Videos
- QUESTION FROM STD. IXBOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics
14 Videos
- STATISTICSBOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-6
21 Videos
Similar Questions
Knowledge Check
In the figure, PQ = QR = RS = SP = SQ = 6 cm and PT = RT = 14 cm. The length of ST (in cm) is
 A4√10B(7√3−2)C10D11
A4√10B(7√3−2)C10D11In a triangle ABC point D and E lie on the sides AB and AC, respectively. Lines segments DC and BE intersect inside the triangle at O. The area of △BOC=8sq.cm,△BDO=7sq.cm and △CEO=4sq.cm. Find the area of quadrilateral ADOE.
AA)21 sq. cmBB)28 sq. cmCC)25 sq. cmDD)19 sq. cm
In the adjoining figure, if PA=10 cm, then find the perimeter of ΔPCD.
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

View SolutionIn the adjoining figure: ∠PSQ=90∘ , PQ= 10 cm , QS = 6cm and RQ = 9cm . Calculate the length of PR.
View SolutionIn figure, DE || BC. IF DE = 3 cm, BC = 6 cm and area of ΔADE=15 sq. cm, then the area of ΔABC is
View SolutionThe length of one pair of opposite sides of a square is increased by 5 cm on each side; the ratio of the length and the breadth of the newly formed rectangle becomes 3 : 2. What is the area of the original square? (a) 25 sq. cm (b) 81 sq. cm (c) 100 sq. cm (d) 225 sq. cm (e) None of these
View SolutionIf the area of a triangle is 100sq,cm,r1=10cm and r2=50cm, then find the value of (b−a)
View Solution