यदि किसी त्रिभुज के दो शीर्षो से सम्मुख भुजाओं पर खींचे गये लम्ब समान हो, तो सिध्द कीजिए कि वह त्रिभुज समद्विबाहु होता है |
दिया है: ΔABCमें शीर्ष B तथा शीर्ष C से भुजाओं AC तथा AB पर क्रमशः शीर्षलम्ब BE तथा CF इस प्रकार हैं कि BE=CF है |
सिध्द करना है: ΔABCसमद्विबाहु है अर्थात AB=AC
उपपत्ति: ΔABEतथा ΔACFमें
∠AEB=∠AFC [प्रत्येक 90∘के बराबर]
∠BAE=∠CAF [उभयनिष्ठ कोण]
तथा, BE=CF [दिया है]
अतः कोण-कोण-भुजा सर्वागसमता कसौटी से
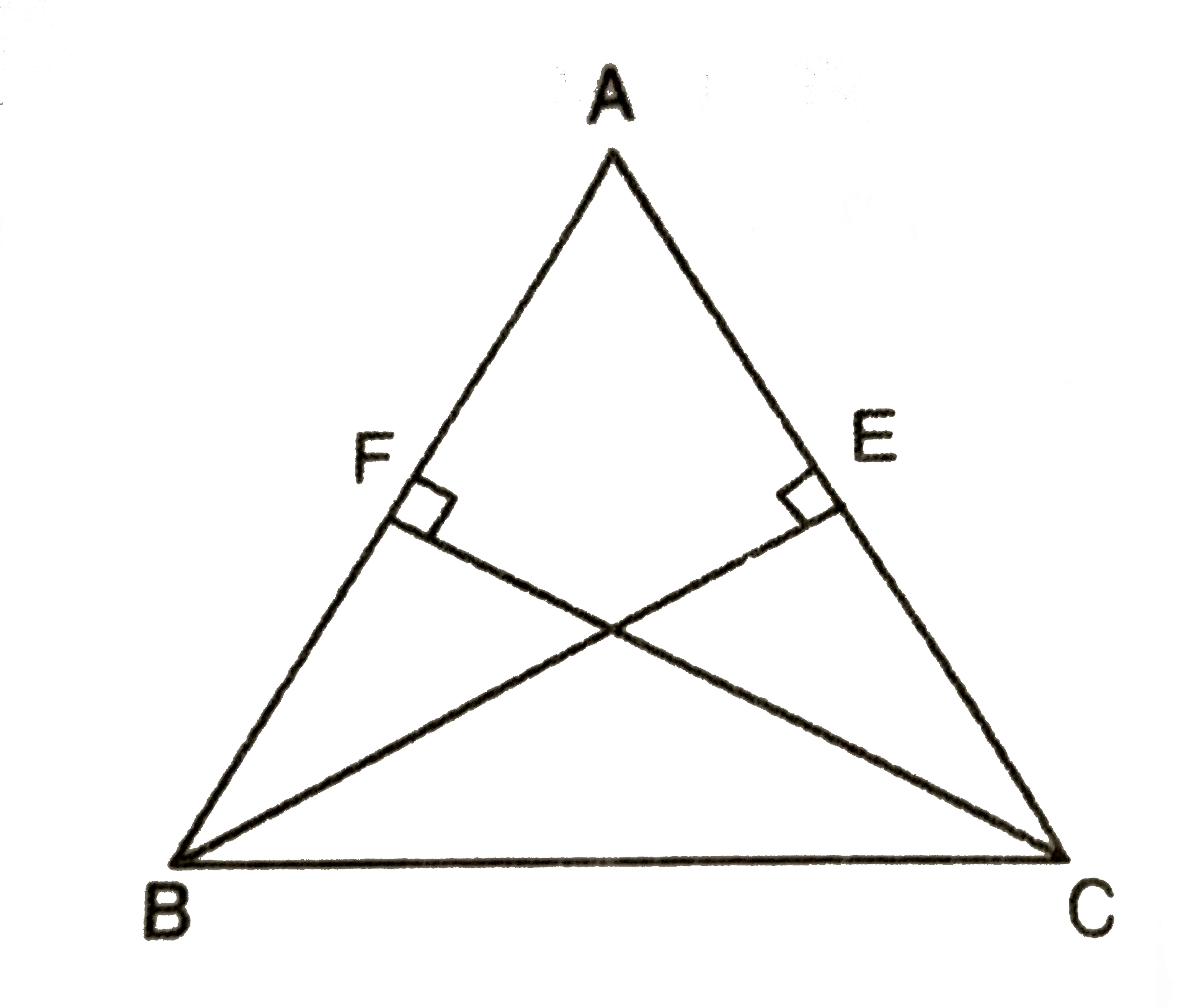
ΔABE≅ΔACF
⇒ AB=AC [∵ सर्वांगसम त्रिभुजों के संगत भाग समान होते है]
अतः ΔABCसमद्विबाहु त्रिभुज है |
Topper's Solved these Questions
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - प्रश्नावली 10.1
13 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - प्रश्नावली 10.2
3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- सांखि्यिकीय आँकड़ों का सारणीयनBOOK - RD SHARMACHAPTER - सांखि्यिकीय आँकड़ों का सारणीयनEXERCISE - बहु विकल्पीय प्रश्न
10 Videos
Similar Questions
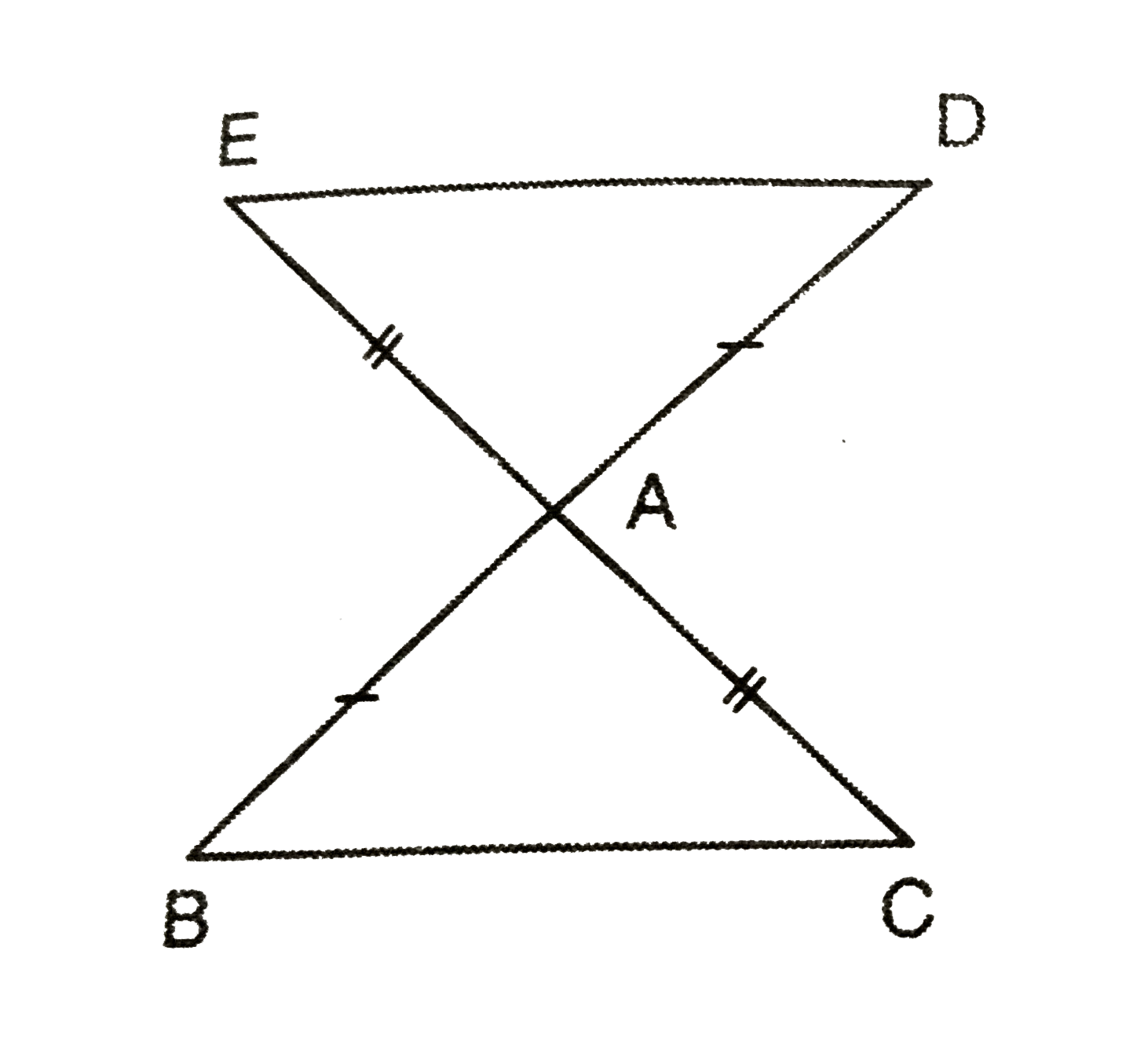
भुजाएँ BA तथा CA तथा इस प्रकार बढ़ाई गई कि BA=AD तथा CA=AE हैं | सिध्द कीजिए कि रेखाखण्ड DE∣∣BC है |
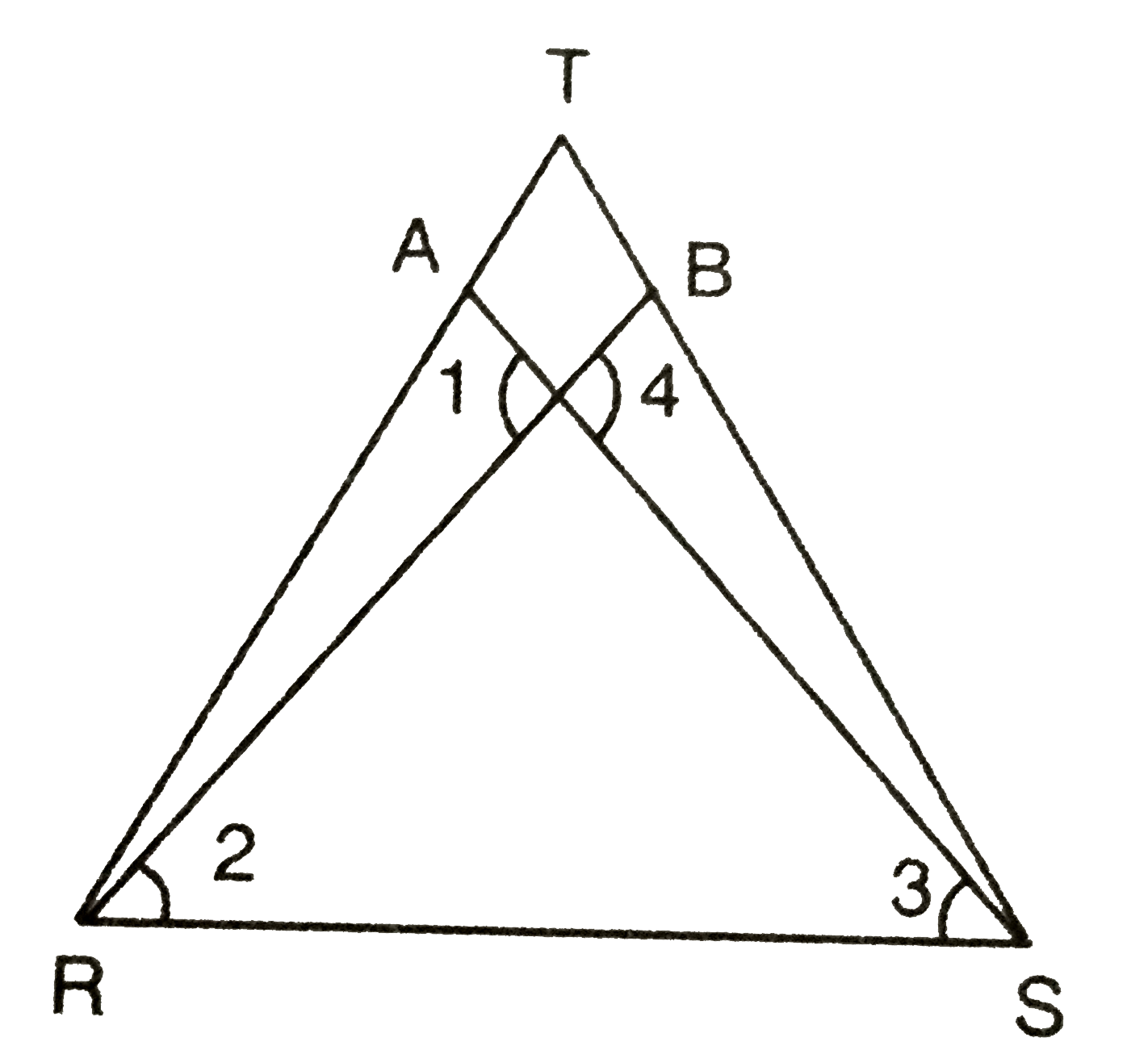
View Solutionयह दिया है RT=TS ∠1=2√3 तथा ∠4=2Sqrt(3)तो, दर्शाइए कि ΔRBT≅ΔSAT
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionप्रेक्षणो के सग्रह में से उच्चतम एव न्यूनतम प्रेक्षणो के अन्तर को कहते है ?
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्ष (0,0),(1,2) तथा (−3,3) है , तो शीर्षो से सम्मुख भुजाओ पर डाले गये लम्बो कि लम्बाई ज्ञात कीजिए
View Solutionकिसी त्रिभुज के शीर्षो से समान दूरी पर स्तिथ बिंदु का नाम लिखि।
View Solutionयदि सदिश 10¯i−5¯j+10¯k किस त्रिभुज के आधार को निरूपित करता है तथा इस आधार की सम्मुख शीर्ष से दूरी 8 मात्रक हो तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionदिखाइए कि किसी त्रिभुज में भुजाओं के लम्ब अर्धक संगामी होते हैं |
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionयदि किसी त्रिभुज के शीर्षो के स्थिति सदिश क्रमश: →a,→b,→c हो तो इस त्रिभुज के केन्द्रक का स्थिति सदिश होगा -
View Solutionयदि किसी त्रिभुज की भुजाओं के मध्य - बिंदुओं के निर्देशांक (2,1),(−1,−3) और (4,5) हों , तो उसके शीर्षों के निर्देशांक ज्ञात कीजिए ।
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solution
