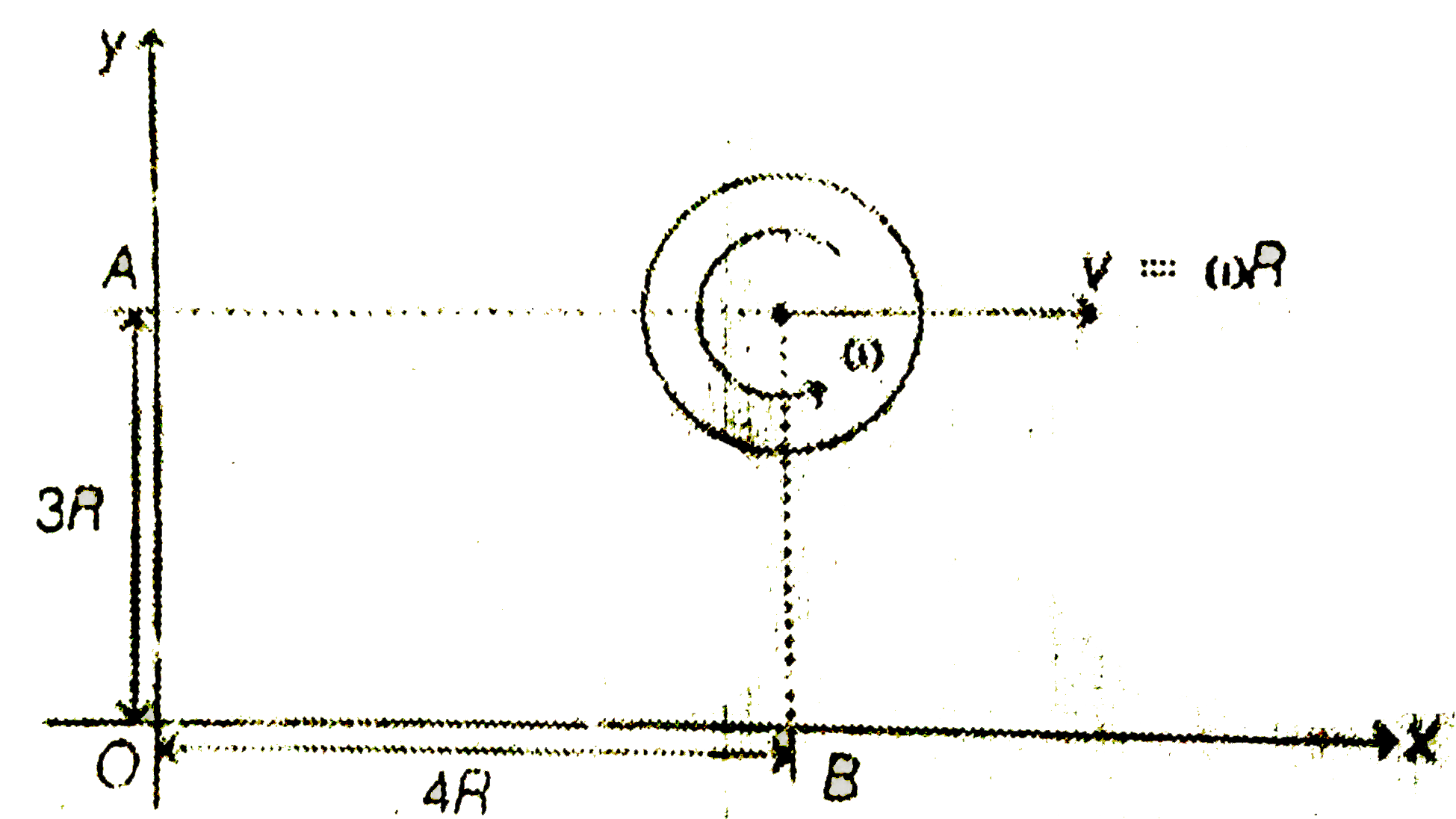
A disc of mass M and radius R is rolling with angular speed ω on a horizontal plane as shown in figure. The magnitude of angular momentum of the disc about the origin O is
(1/2)Mg2ω
MR2ω
(3/2)MR2ω
2MR2Ω
The correct Answer is:C
L=MVR+Iω
here V=ΩR,I=MR22
L=M(Rω)R+MR22ω=32MR2ω
Topper's Solved these Questions
Similar Questions
A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View Solution
Knowledge Check
A disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A(1/2)MR2ωBMR2ωC(3/2)MR2ωD2MR2ωA disc of mass m and radius R moves in the x−y plane as shown in Fig. The angular momentum of the disc about the origin O at the instant shown is
 A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆk
A−52mR2ωˆkB73mR2ωˆkC−92mR2ωˆkD52mR2ωˆkA uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.
 Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0
Aincreases continuously as the disc moves awayBdecreases continuously as the disc moves awayCis always equal to 2MRv0Dis always equal to MRv0

A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
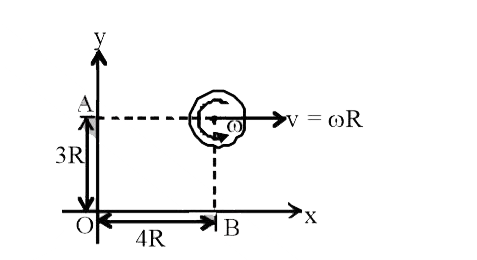
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
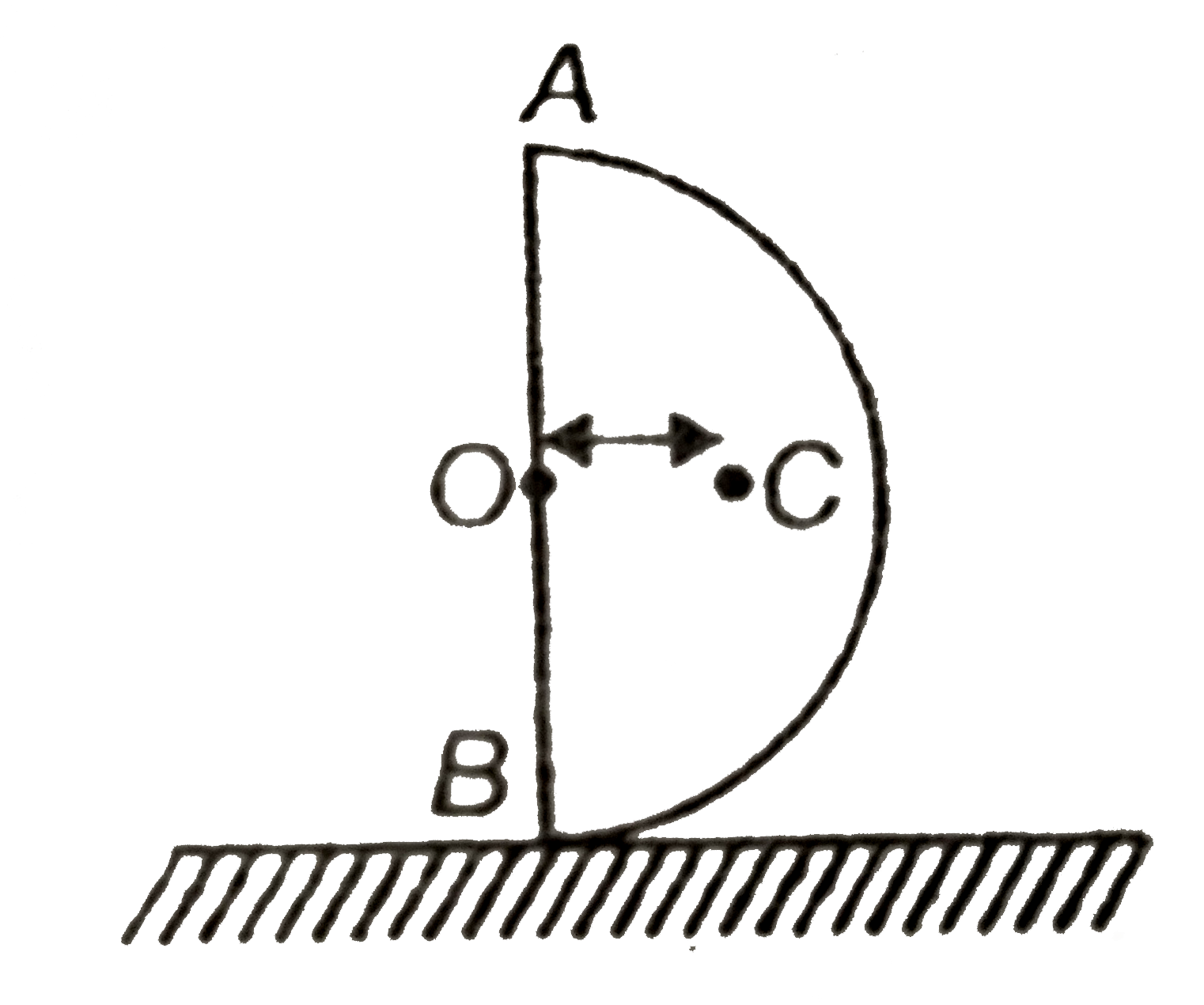
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
View SolutionA disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View Solution
