The graph of the function y=f(x) has a unique tangent at the point (ea,0) through which the graph passes then lim–––––(x→ea)loge{1+7f(x)}−sinf(x)3f(x)
1
2
7
None of these
The correct Answer is:B
Step by step video, text & image solution for The graph of the function y = f(x) has a unique tangent at the point (e^a,0) through which the graph passes then lim__(x->e^a) (log_e {1+7f (x)} - sin f(x))/(3f(x)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
40 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
If the graph of the function y=f(x) has a unique tangent at the point (a,0) through which the graph passes, then evaluate (lim)x→a(log)e{1+6f(x)}3f(x)
View SolutionThe graph of the function y=f(x) has a unique tangent at the point (a, 0) through which the graph passes then, limx→a(ln(1+6f(x))3f(x)
View Solution
Knowledge Check
If the graph of the function y = f(x) passes through the points (1, 2) and (3, 5), then ∫31f'(x)dx=
A1B2C3D4If the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isA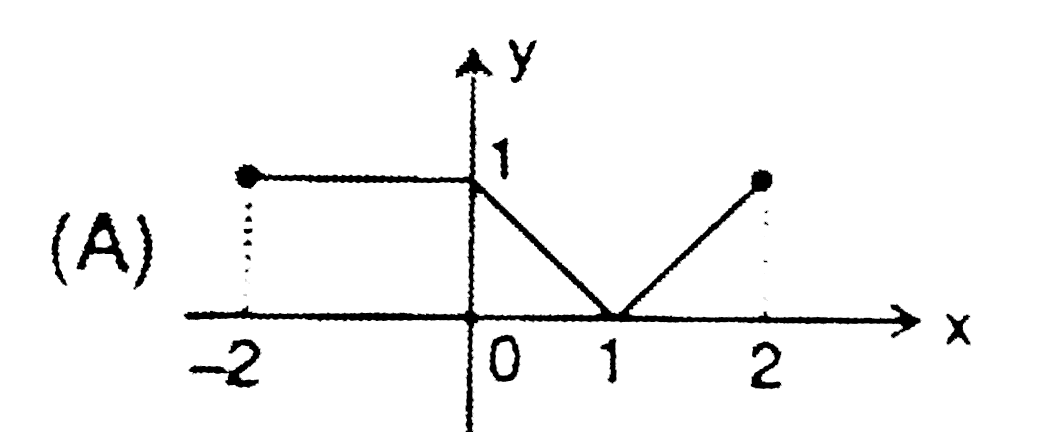 B
B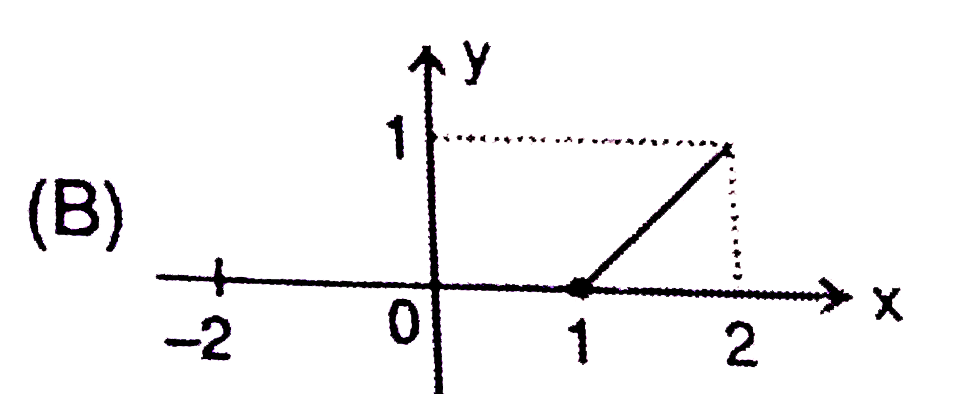 C
C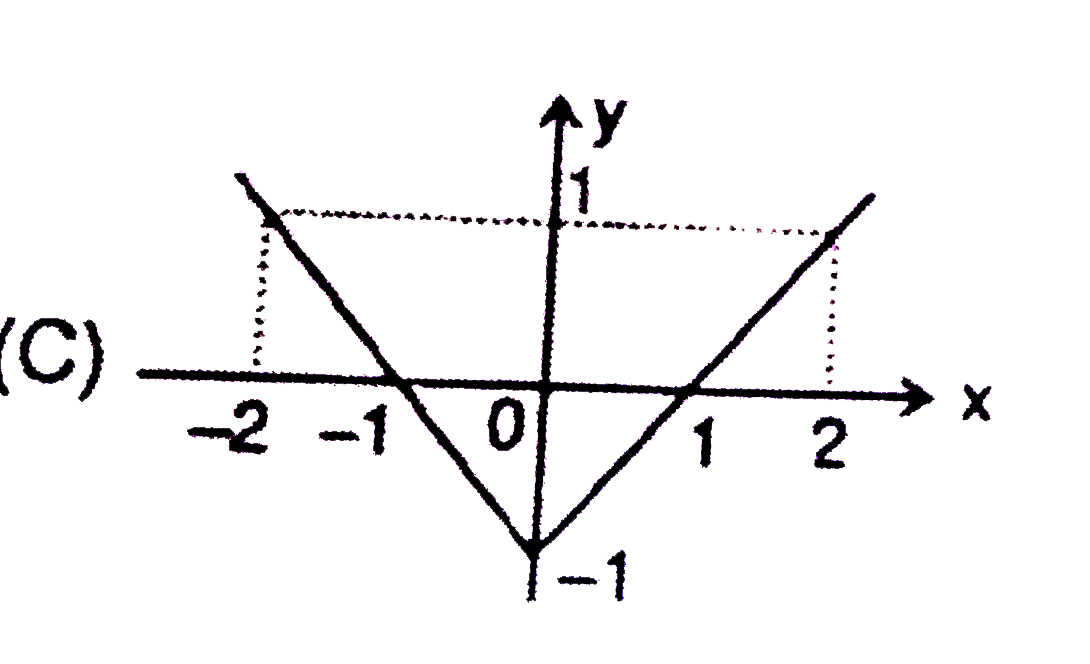 D
D
Statement-1: If the graph of the function y=f(x) has a unique tangent at the point (a,0) through which limx→aloge(1+6(f(x)))3f(x)=2 Statement-2: Since the graph passes through (a,0). Therefore f(a)=0. When f(a)=0 given limit iszero by zero form so that it can be evaluate by using L-Hospital's rule.
View SolutionIf the graph of the function y=f(x) has a unique tangent at point (ea,0) (not vertical, non-horizontal) on the graph, then evaluate limx→ea(1+9f(x))−tan(f(x))2f(x).
View SolutionMark the graph of the function
f(x)=3ex+5−7
View SolutionDraw the graph of the function f(x)=2x2−loge|x|
View SolutionIf the graph of the function y=f(x) is as shown : the graph of y=12(|f(x)|−f(x)) is
View SolutionIf graph of the function y=f(x) is continuous and passes through point (3,1) then (lim)x→3(log)e(3f(x)−2)2(1−f(x)) is equal 32 b. 12 c. −32 d. −12
View Solution
