C1 is a curve y2=4x,C2 is curve obtained by rotating C1,120∘ in anti -clockwise direction C3 is reflection of C2 with respect to y=x and S1,S2,S3 are foci of C1,C2 and C3, respectively, where O is origin.
If (t2,2t) are parametric form of curve C1, then the parametric form of curve C2 is
=(12(t2+2√3t),12(√3t2+2t))
=(12(−t2+2√3t),12(√3t2+2t))
=(12(−t2+2√3t),12(−√3t2+2t))
=(12(−t2+2√3t),12(−√3t2−2t))
The correct Answer is:D
Step by step video, text & image solution for C_1 is a curve y^2=4x,C_2 is curve obtained by rotating C_1,120^@ in anti -clockwise direction C_3 is reflection of C_2 with respect to y=x and S_1,S_2,S_3 are foci of C_1,C_2 and C_3, respectively, where O is origin. If (t^2,2t) are parametric form of curve C_1, then the parametric form of curve C_2 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PARABOLABook:ARIHANT MATHSChapter:PARABOLAExercise:Exercise (Single Integer Answer Type Questions)
Explore 10 Videos
- PARABOLABook:ARIHANT MATHSChapter:PARABOLAExercise:Exercise (Statement I And Ii Type Questions)
Explore 8 Videos
- PARABOLABook:ARIHANT MATHSChapter:PARABOLAExercise:Exercise (More Than One Correct Option Type Questions)
Explore 15 Videos
- PAIR OF STRAIGHT LINES Book:ARIHANT MATHSChapter:PAIR OF STRAIGHT LINES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 2 Videos
- PERMUTATIONS AND COMBINATIONS Book:ARIHANT MATHSChapter:PERMUTATIONS AND COMBINATIONS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 28 Videos
Similar Questions
Knowledge Check
C1 is a curve y2=4x,C2 is curve obtained by rotating C1,120∘ in anti -clockwise direction C3 is reflection of C2 with respect to y=x and S1,S2,S3 are foci of C1,C2 and C3, respectively, where O is origin.
Area of ΔOS2S3 isA18B14C12D1C1 is a curve y2=4x,C2 is curve obtained by rotating C1,120∘ in anti -clockwise direction C3 is reflection of C2 with respect to y=x and S1,S2,S3 are foci of C1,C2 and C3, respectively, where O is origin.
IF S1(x1,y2),S2(x2,y2) and S3(x3,y3) then the value of ∑x21+∑y21 isA2B3C4D5If the joining the points (0,3) and (5,-2) is a tangent to the curve y=cX+1, then value of c is -
A1B-2C4D-4
The line joining the points (0,3) and (5,-2) becomes tangent to the curve y=cx+1 then c=
View SolutionA wave is represented by an eqution y=c1sin(c2x+c3t). In which direction is the wave going? Assume that c1,c2andc3 are all positive.
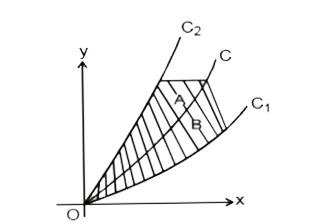
View SolutionLet C1andC2 be two curves passing through the origin as shown in the figure. A curve C is said to ‘‘bisect the area’’ the region between C1andC2, if for each point P of C, the two shaded regions A and B shown in the figure have equal areas. Determine the upper curve C2, given that the bisecting curve C has the equationy=x2 and that the lower curve C1 has the equation y=x2/2.
View SolutionThe differential equation which represents the family of curves y=c1ec2x, where c1andc2 are arbitrary constants is
View SolutionThe differential equation representing the family of curves y2=2c(x+c2/3), where c is a positive parameter is of
View Solution

