Show that the triangle, the coordinates of whose verticles are given by integers, can never be an equilateral triangle.
The correct Answer is:c=±b√3
Step by step video, text & image solution for Show that the triangle, the coordinates of whose verticles are given by integers, can never be an equilateral triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHSCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHSCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHSCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
In the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
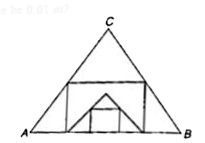 Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of these
Aa. (873−504√3)cm2Bb. (738−504√3)cm2Cc. (873−405√2)cm2Dd. none of theseIn the given figure, ΔABC is an equilateral triangle. Find ∠BEC :
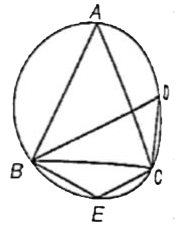 A120∘B60∘C80∘Dnone of the above
A120∘B60∘C80∘Dnone of the above
If the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf (-4,3) and (4,3) are two vertices of an equilateral triangle, then find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
View SolutionIn the given figure, OP is equal to the diameter of the circle. Prove that △ABP is an equilateral triangle.
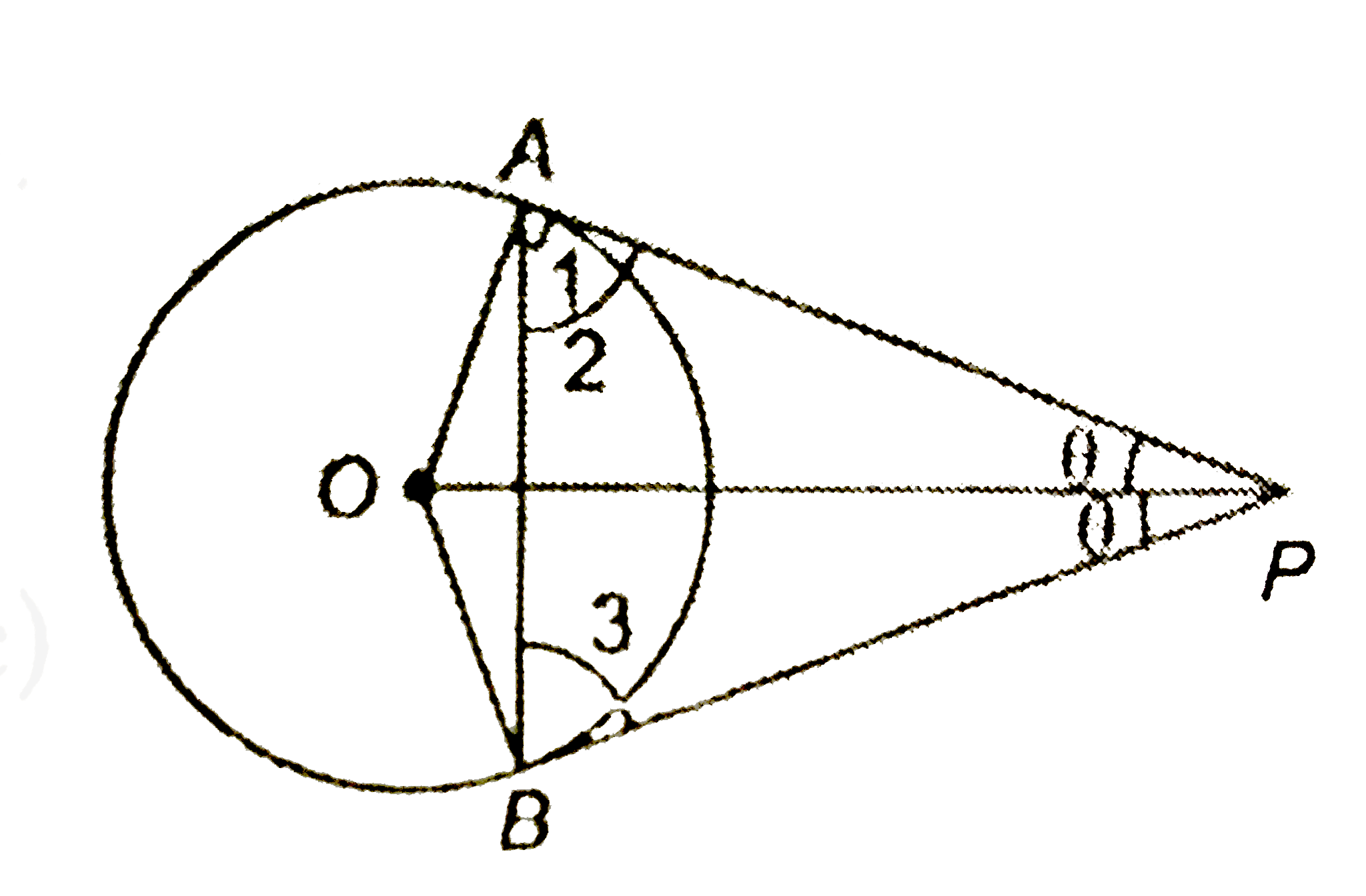
View SolutionIf the vertices of a triangle have integral coordinates, prove that the trinagle cannot be equilateral.
View SolutionFind the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View SolutionShow that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
View Solution
