Give the number of stereoismoers of (A) in the following reactions.
a. (A)(C7H12)O3/oxid.−−−−−→Acetone(B)+Oxalicacid(C)+Aceticacid(D)
b. (A)(C8H14)O3/oxid.−−−−−→Butane−2−ene(B)+Oxalicacid(C)+Aceticacid(D)
c. (A)(C6H10)O3/oxid.−−−−−→Oxalicacid(B)+Aceticacid(C)
d. (A)(C9H16)O3/oxid.−−−−−→Butane−2−one(B)+Pyruvicacid(C)+Aceticacid(D)
e. (A)(C10H18)O3/oxid.−−−−−→Butane−2−one(B)+Pyruvicacid(C)+Propanoicacid(D)
In all the problem :
1. The aldehydes obtained in reductive ozonolysis are converted to acids in oxidative ozonolysis and ketones remain unchanged. So, firest convert acids into aldehyde and find the structure of (A).
2. Keep the bi− functional compound in centre and other two compounds on either side with their functional groups facing each other.
3. If bi− functional compound is symmetrical, e.g., oxalic acid, one structural isomer will be obtained.
4. If bi− functional compoound is unsymmetrical, e.g., pyruvic acid, two structural isomers will be obtained.
5. Compound (A) in all the parts has 2∘ of unsaturation and three compounds are obtained after ozonolysis, therefore, compound (A) in all the parts has two (C=C) bonds, i.e., all are dienes.
a. 
Compound (A) shows geometrical isomers around C4−C5 double bond since the two groups around C−4 and C−5 are different but do not show geometrical isomers around C2−C3 double bond since the two groups around C−2 are the same.
Number of stereoismers for (A)=2

b. Proceed in the same manner as in (a).
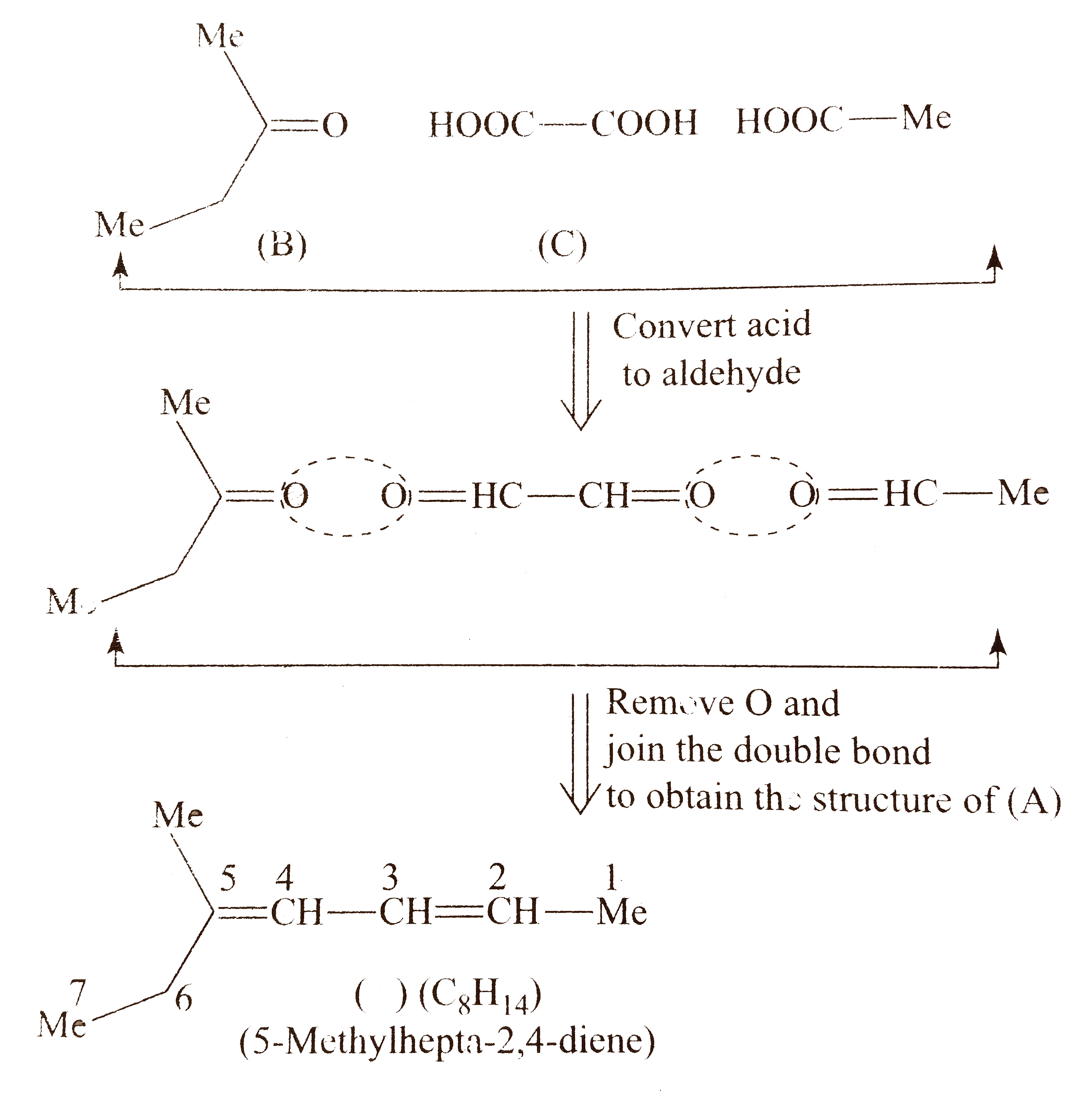
Compound (A) shows geometrical isomer around both (C2−C3) and (C4−C5) double bonds since two of the groups around these bonds are different. Moreover, terminal groups (−CH3) and (−C2H5), around C2 and around C5 , respectively, are different.
Number of G.I. when the terminal groups are different =2n, wheren is the number of double bonds (two double bonds).
∴G.I.=22=4
Number of stereoismoers of (A)=4
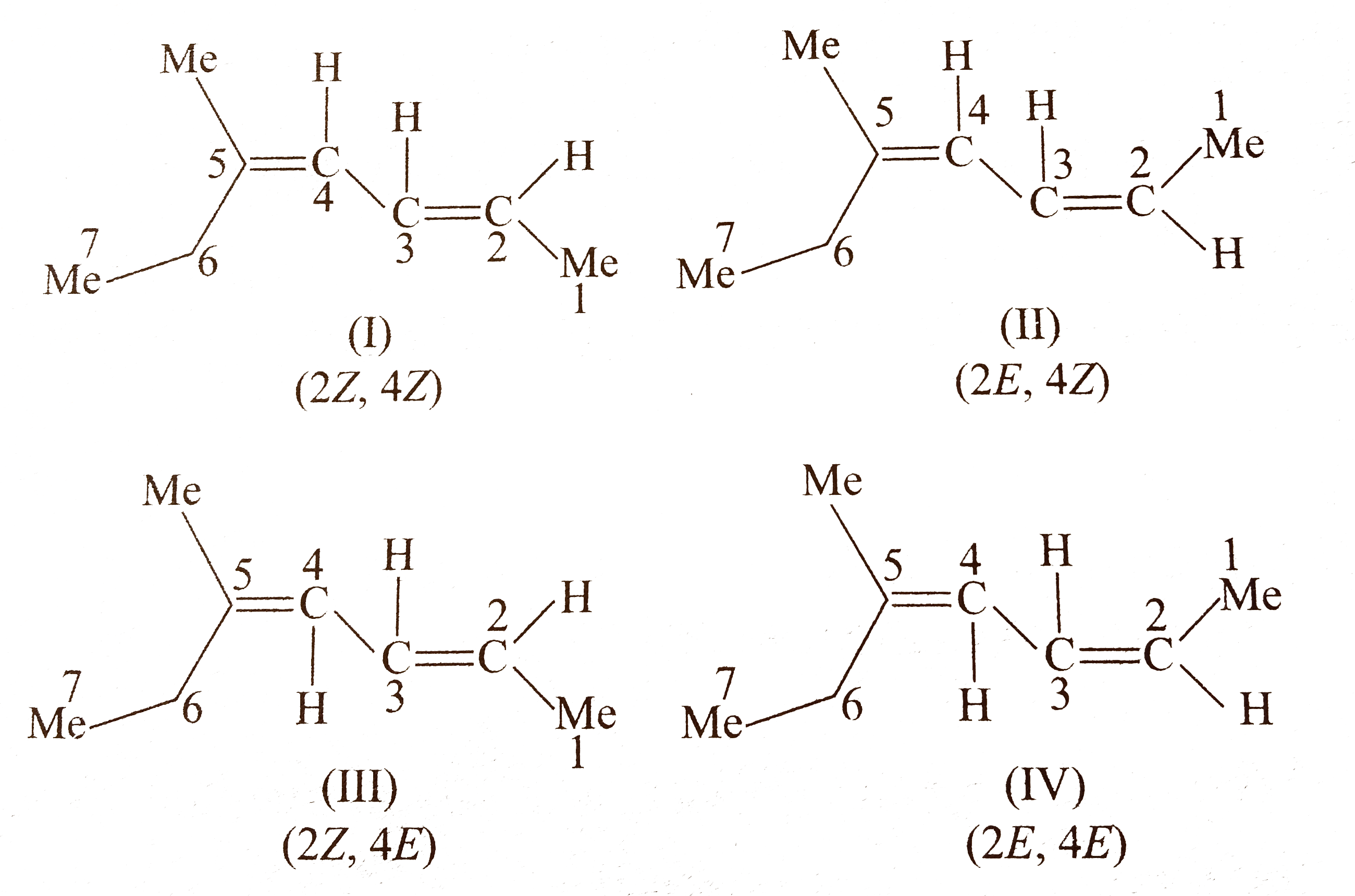
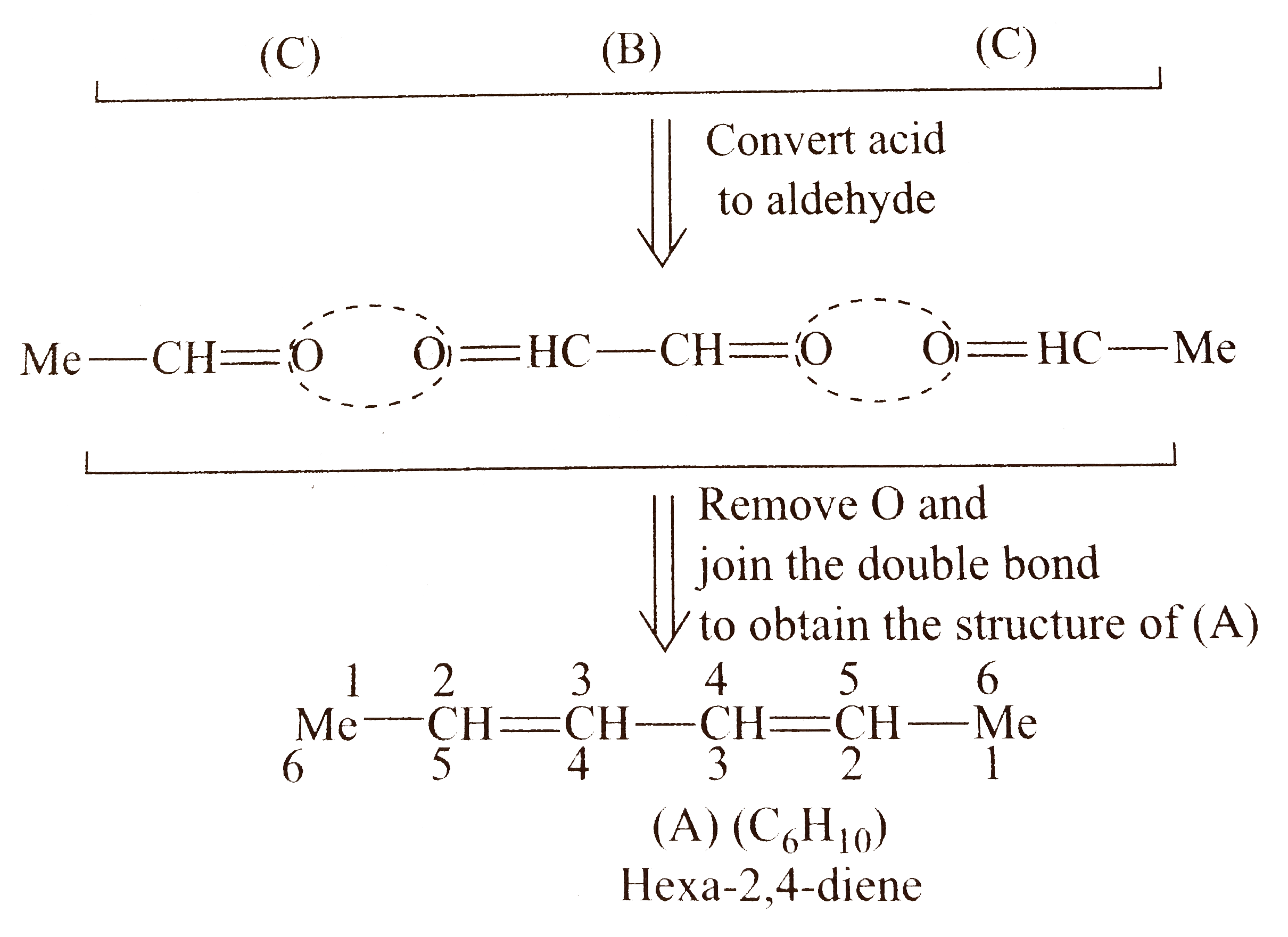
c. Proceed in the same maner as in (a) and (b)
Total C atoms in (A)=6
Total C atoms in (B)+(C)=4
Therefore, there must be 2mol of monofunctional compoound (C) (acetic acid).
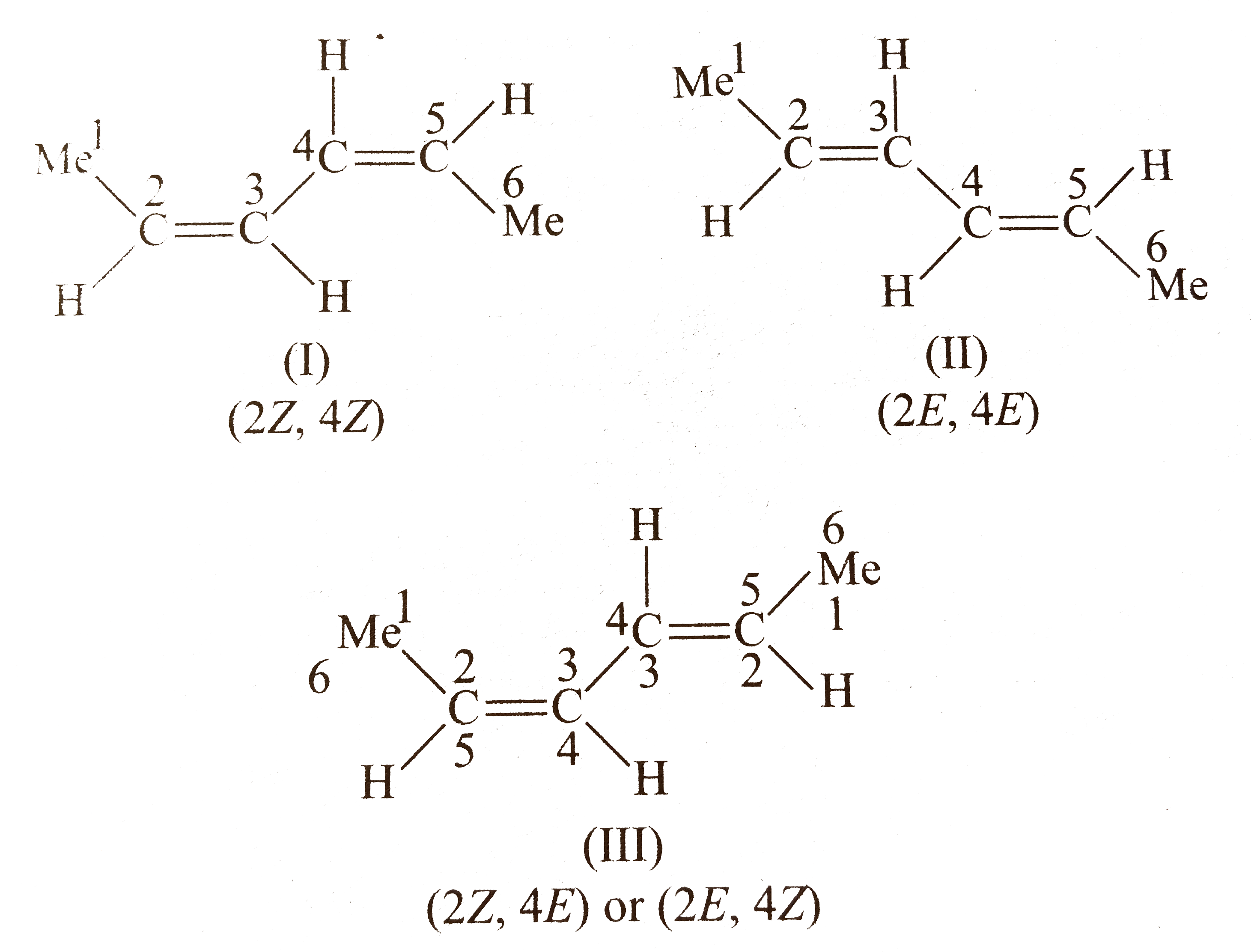
Compound (A) shows geometrical isomerism around both (C2−C3) and (C4−C5) double since the two groups around these double bonds are different. Moreover, the terminal groups around C2 and around C5 are same (methly group).
Number of G.I. when the terminal groups are the same.
=n−12+(n−2)/22, where n is the number of double bonds and n is even.
G.I.=2n−1+22
Number of stereoisomers of (A)=3
(Here,2Z,4Eand 2E,4Z will be the same, since the numbering can be one either way.)
d. Procedd in the same manner as in (a),(b), and (c). Here, the bi - functional group compound (C) is unsymmetrical, therefore, there will be two structureal isomers of (A) and each of them will show stereoisomers.
i. 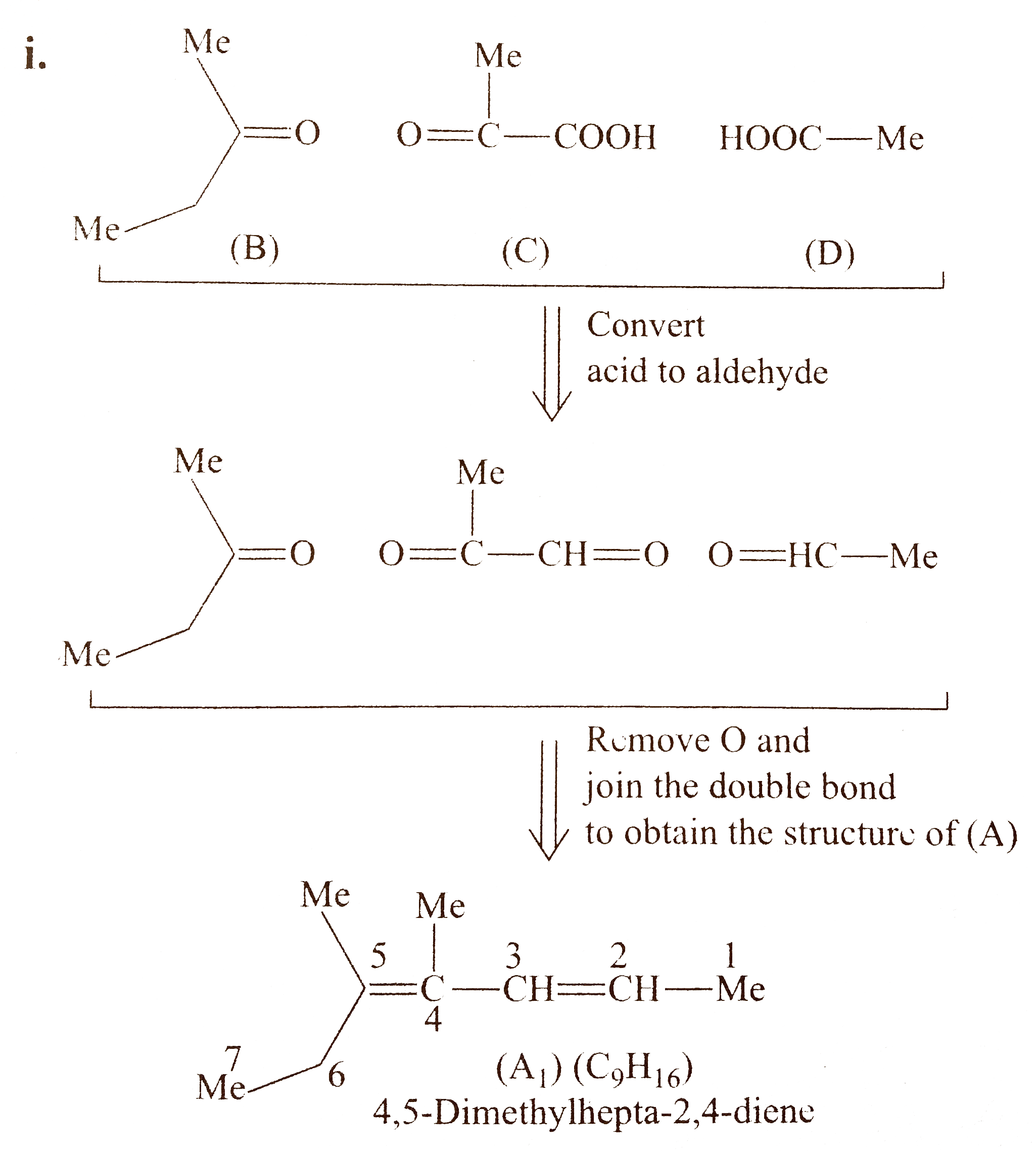
ii. Another structural isomer of (A) is possible, by either changing the position of (B) and (D) or by writing the structure of (C) in another way [pointing (−COOH) group in (C) towards (B)].


Both (A1) and (A2) show geometrical isomers around (C2−C3) and (C4−C5) double bonds, because the two groups around these double bonds are different. Moreover, the terminal groups around C2 and C5 are different (at C−2, one Me and H, at C6 one Me and one Et group) .
Number of G.I. when terminal groups are different =2n=22=4
Hnece, (A) will show four geometrical isomers, similarly, (A2) will also show four geometrical isomers.
Number of stereoisomers for (A)=(A1+A2)=(4+4)=8
Four diastereomers for A1
i. 2X,4Z ii. 2E,4E
iii. 2E,4Z iv. 2Z,4E
e. Proceed in the same manner is in (a). The bi− functional groups compound (C) is uncymmetrical, therefore, there wil be two structural and each of them will show stereoisomers.
i. 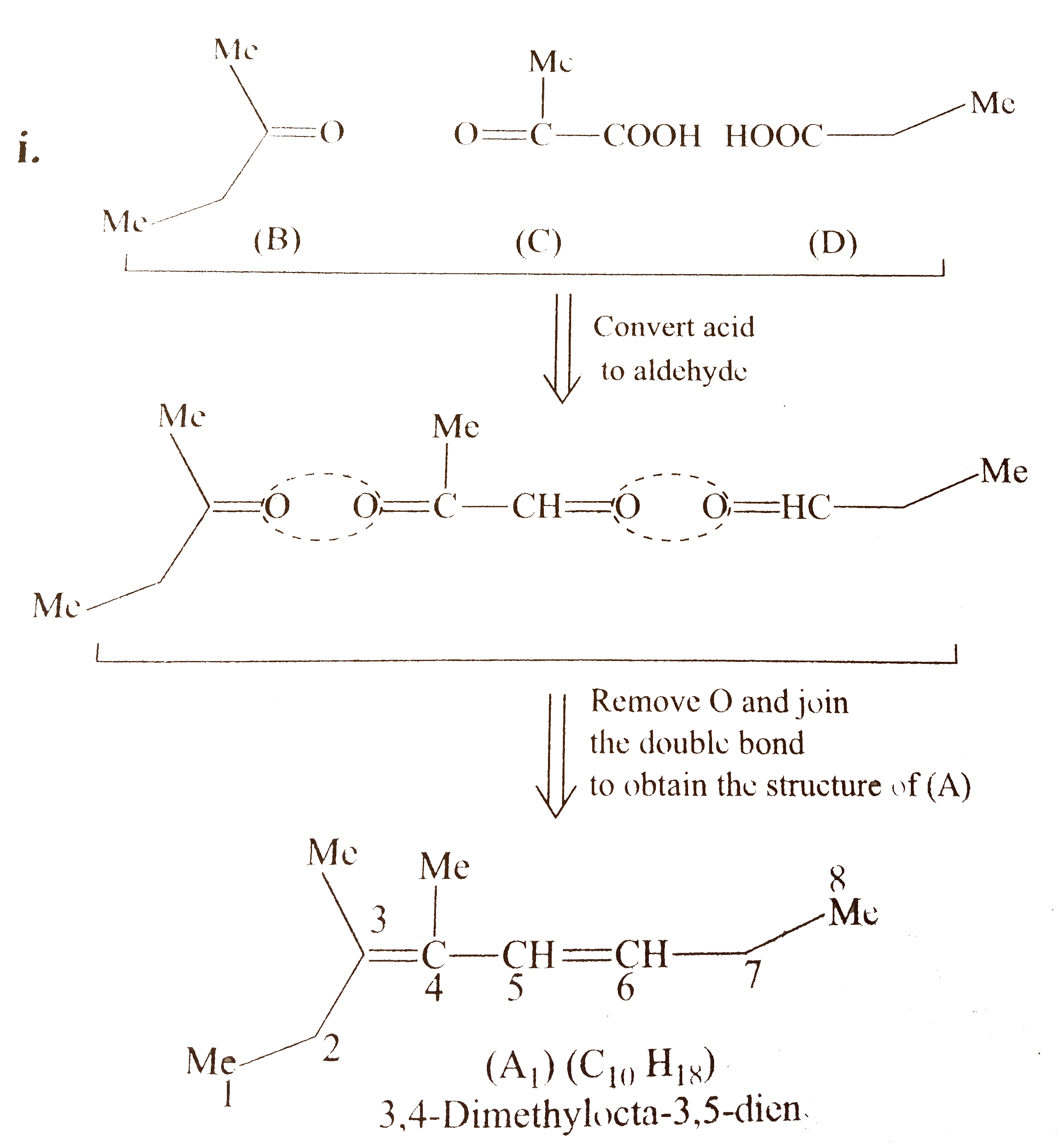
ii. Another structural isomer of (A) is possible by either changing of (B) and (D) or by writing the structure of (C) in another way [ pointing (−COOH) group in (C) towards (B)].
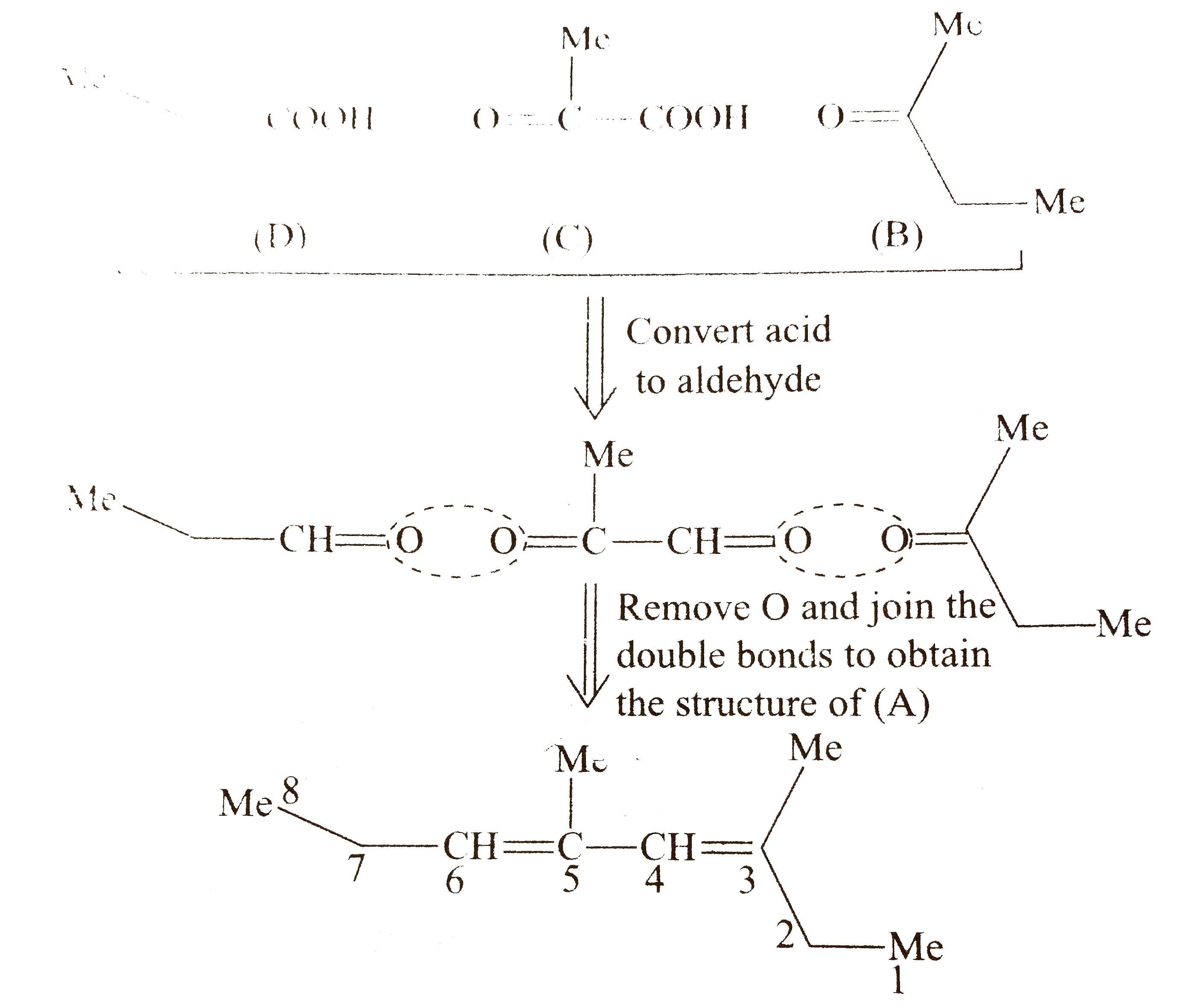
Both (A1) and (A2) show G.I. around (C3−C4) and (C5−C6) double bonds, because the two groups around these double bonds are different. Moreover, the terminal groups C3 and (C6) are different ( at C3, one Me and one Et group, at C6 one Et and one H)
Number of G.I. when the terminal groups are different =22=4.
Number of diastereomers for (A1)=4
number of diastereomers for (A2)=4
Total number of stereoisomers =8
Topper's Solved these Questions
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRYCHAPTER - ALKENES AND ALKADIENESEXERCISE - EXERCISES
29 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRYCHAPTER - ALKENES AND ALKADIENESEXERCISE - linked Comprehension Type
38 Videos
- ALKENES AND ALKADIENESBOOK - CENGAGE CHEMISTRYCHAPTER - ALKENES AND ALKADIENESEXERCISE - Single correct Answer
14 Videos
- ALKANES AND CYCLOALKANESBOOK - CENGAGE CHEMISTRYCHAPTER - ALKANES AND CYCLOALKANESEXERCISE - Archives
13 Videos
- ALKYNESBOOK - CENGAGE CHEMISTRYCHAPTER - ALKYNESEXERCISE - Exercises (Archives - Analytical and Desriptive Type)
4 Videos
Similar Questions
Knowledge Check
CH3CH2OHP+I2−−−→AMg−−→etherBHCHO−−−→CH2O−−→D
The product 'D' is-AButanalBn-butyl alcoholCn-propyl alcoholDPropanal(X)O3/Zn−−−→H2OCO2+CH3−C∣∣O−H+OHC−C∣∣O−CHO
X isA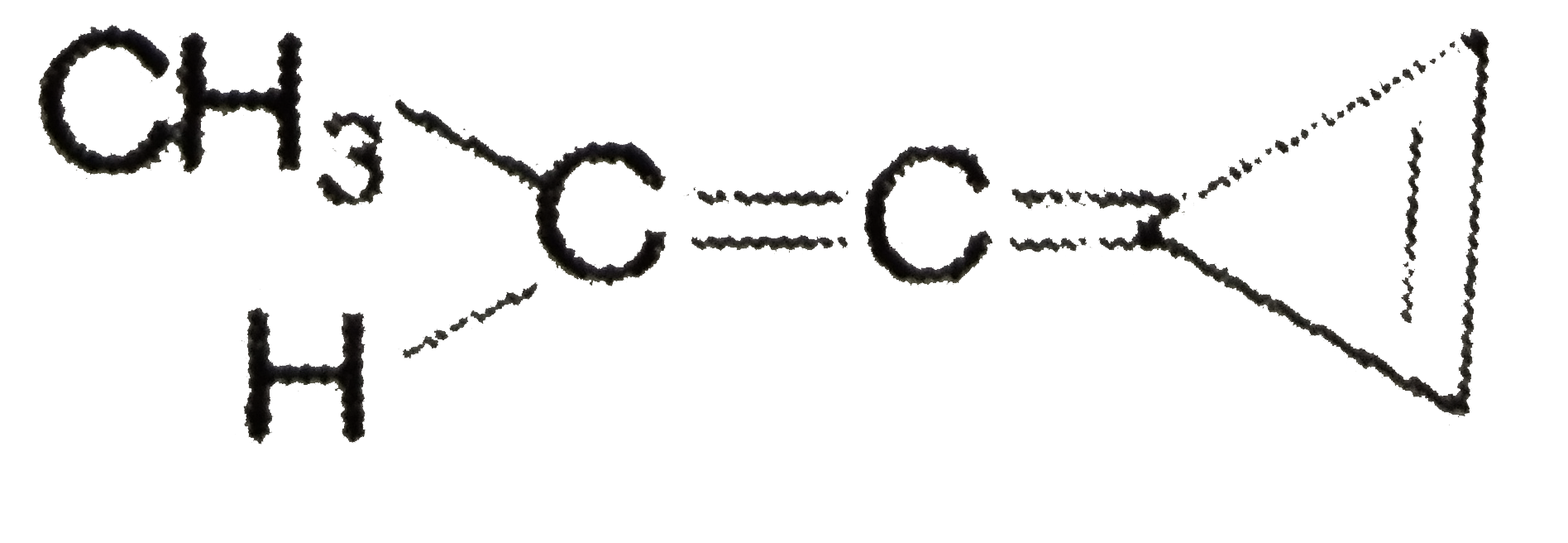 B
B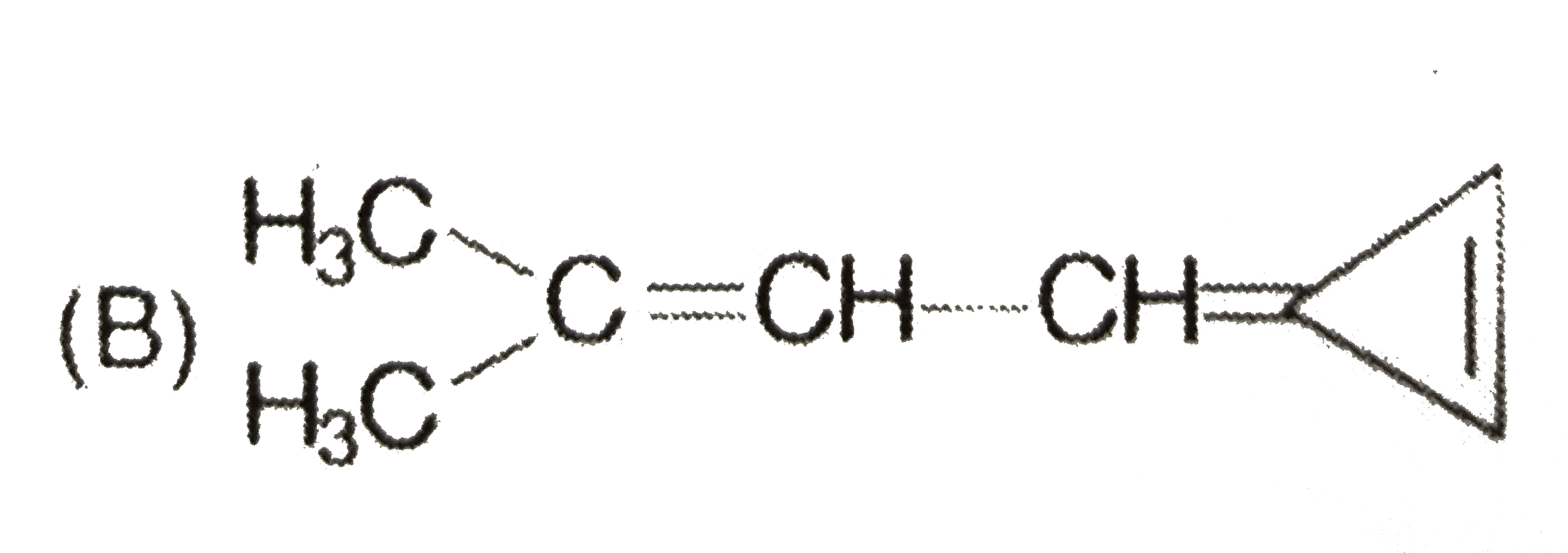 C
C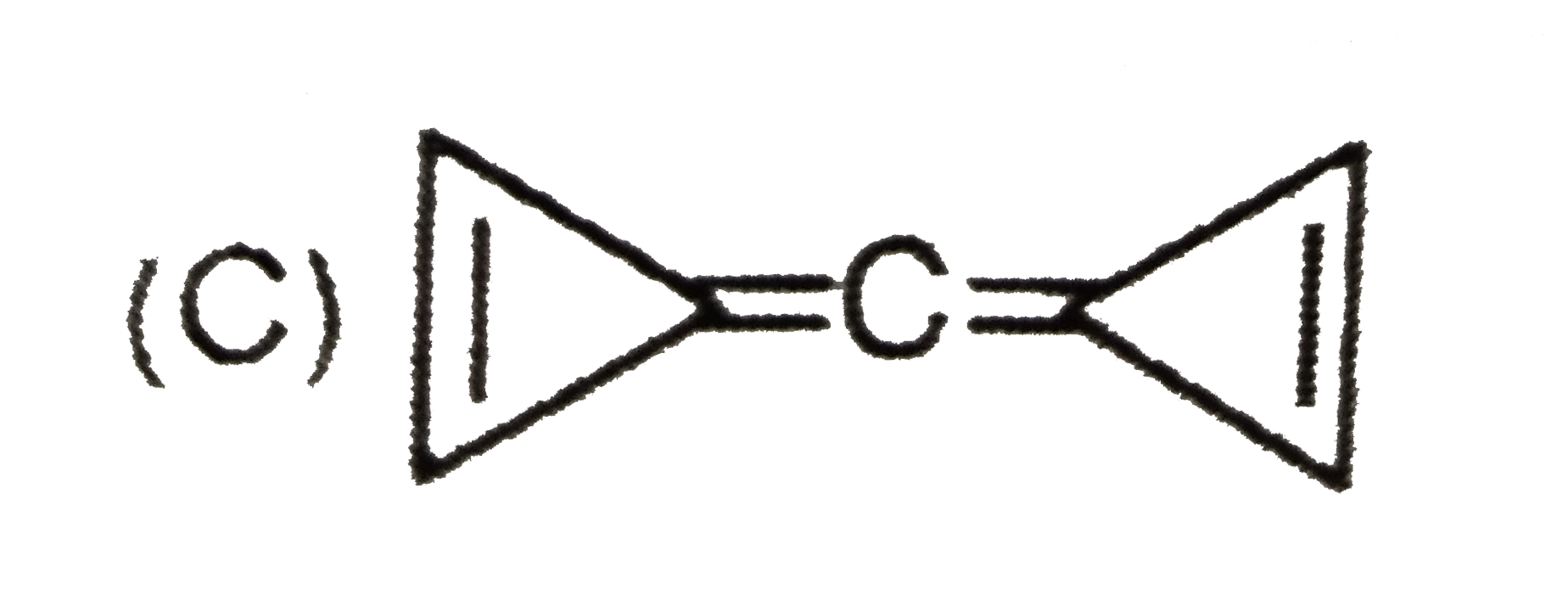 D
D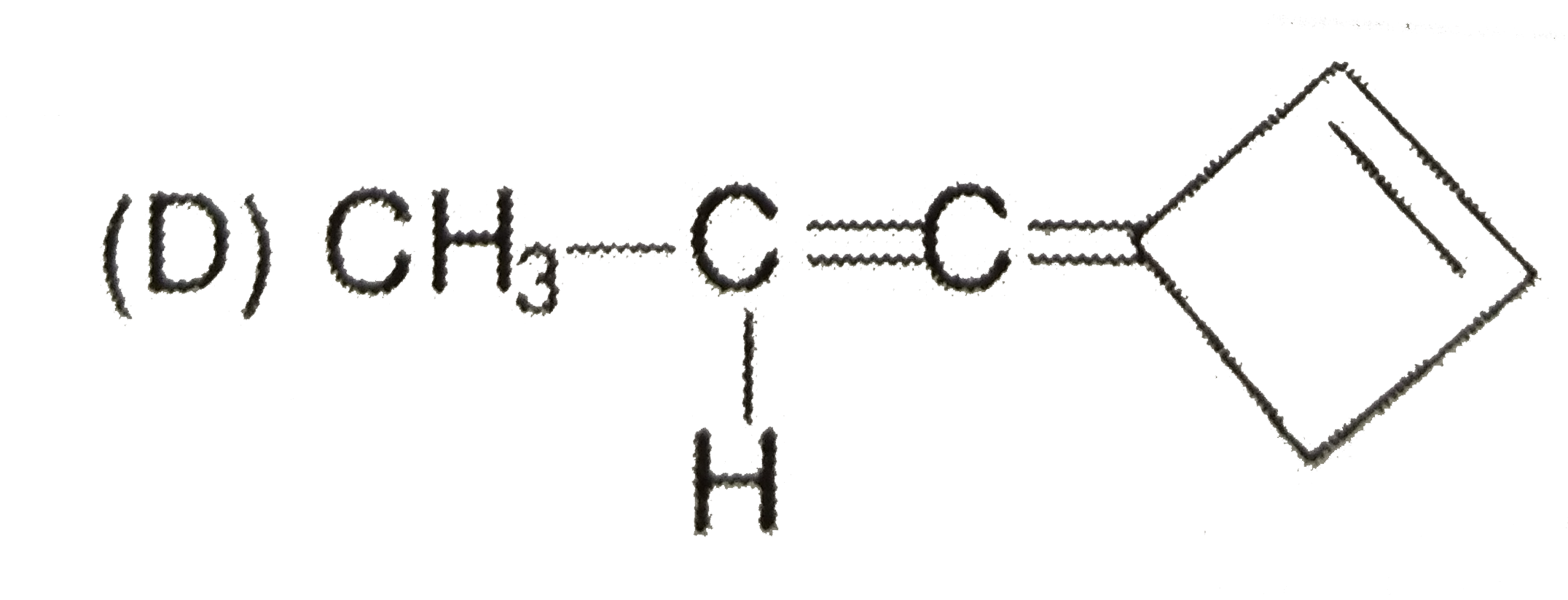
In the reaction, CH3C≡C−CH3(i)X−−−−−−−−−−→(ii)Zn/H2OCH3−C∣∣O−C∣∣O−CH3, X is:
AHNO3BO2CO3DKMnO4
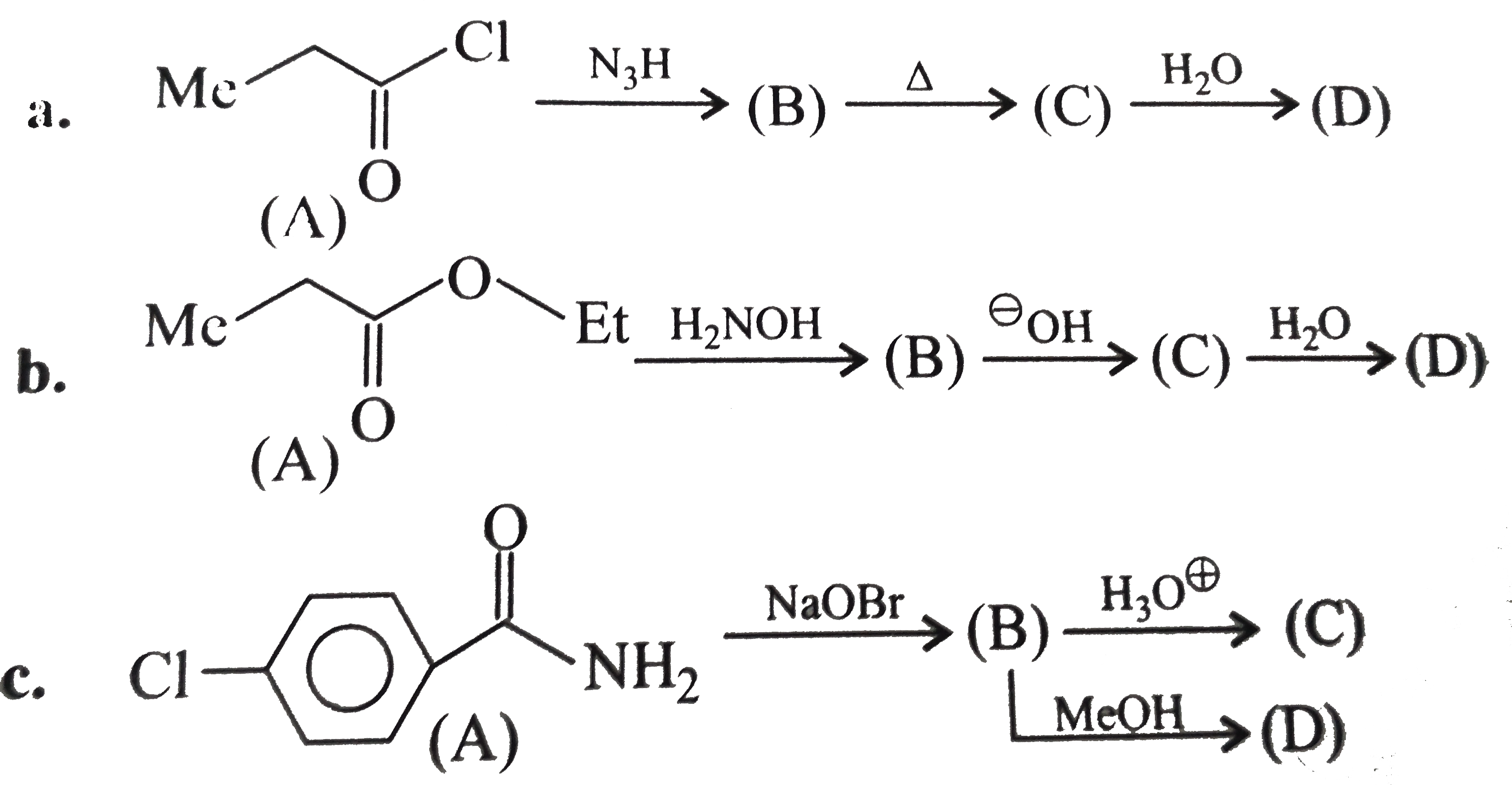
Complete the following reactions
a. PhNH2(A)HNO2−−−→0.5∘C(B)−−−−→DH2PO2(C)
b.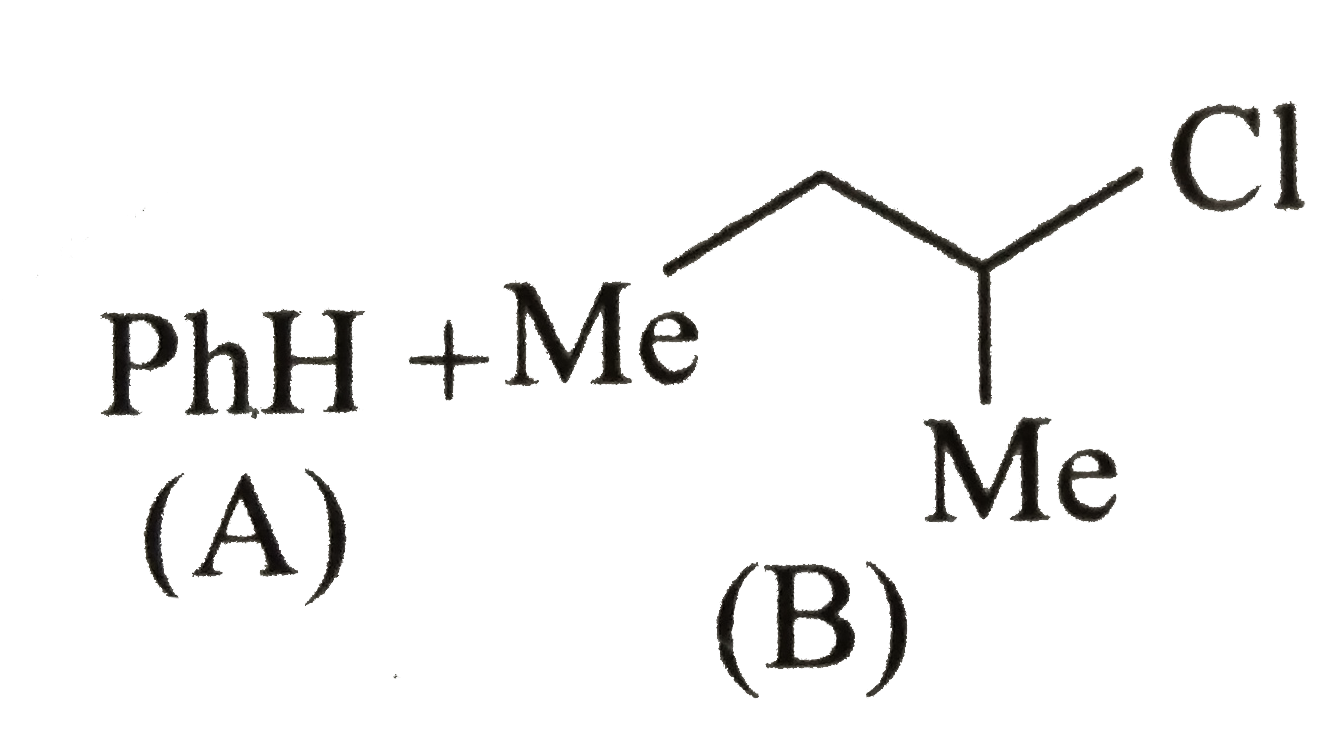
c. PhCH(A)=O+HCN(B)→(C)LAH−−→D
d. PhCH=O(A)+MeNO2(B)ΘOH−−→Fe,FeSO4−−−−−−→H⊕D
e.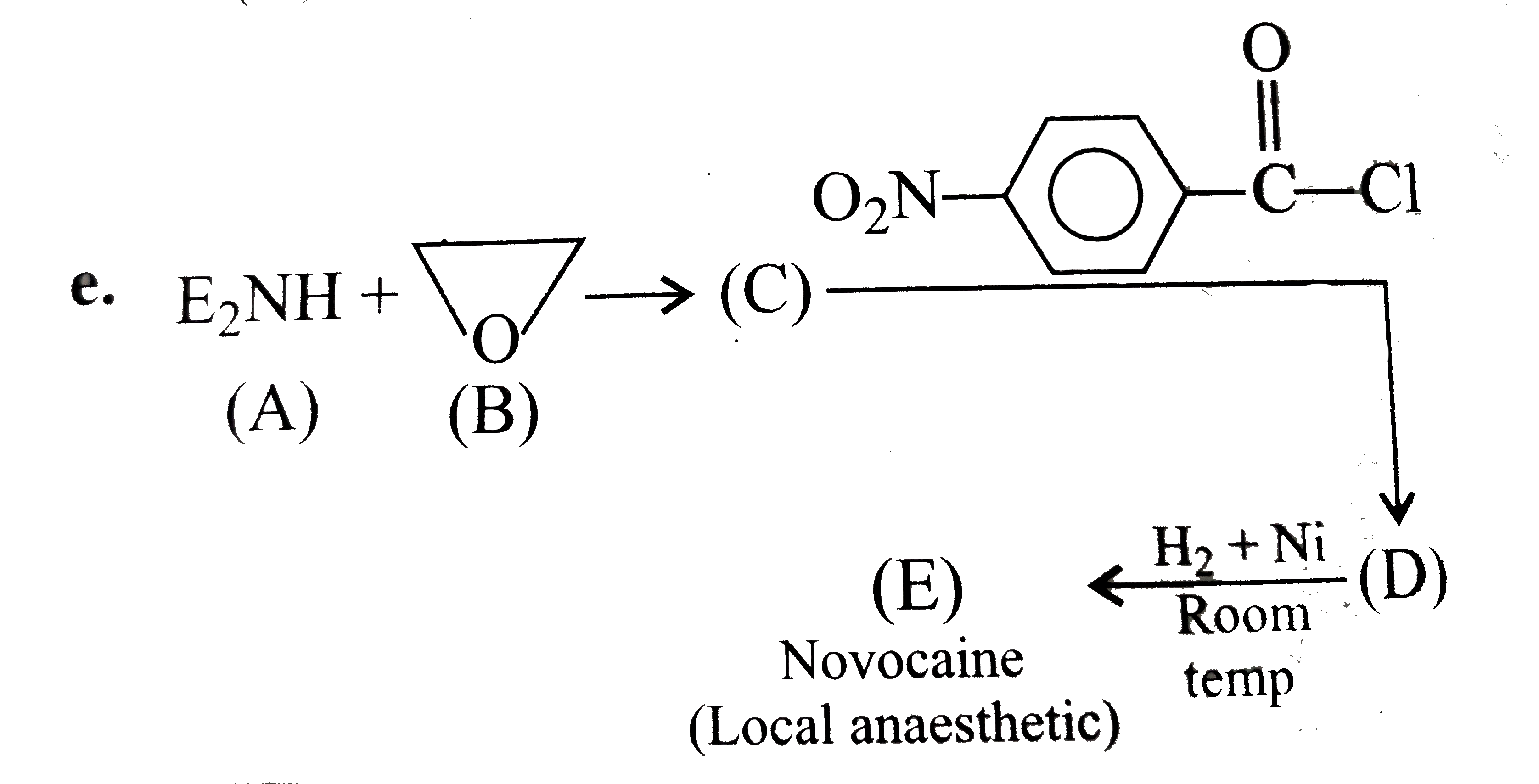
View SolutionComplete the following reactions :
(a) C6H6+Ac2OAlCl3−−→(A)1.Br2/ӨOH−−−−−−→2.H3O⊕(B)
(b)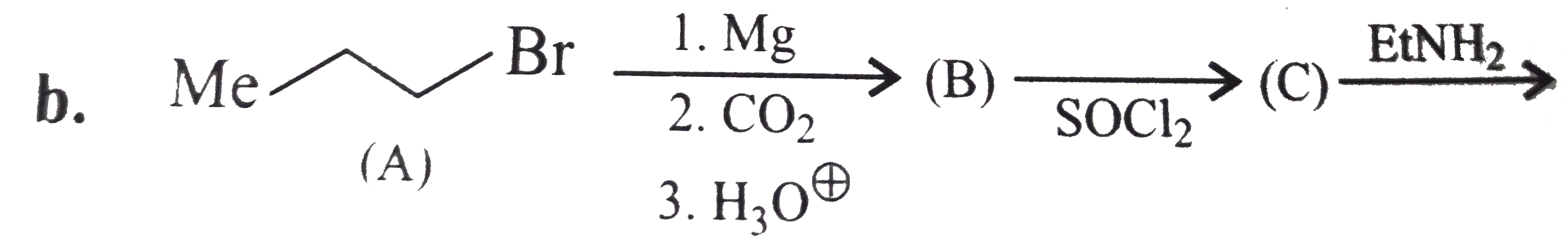
( c)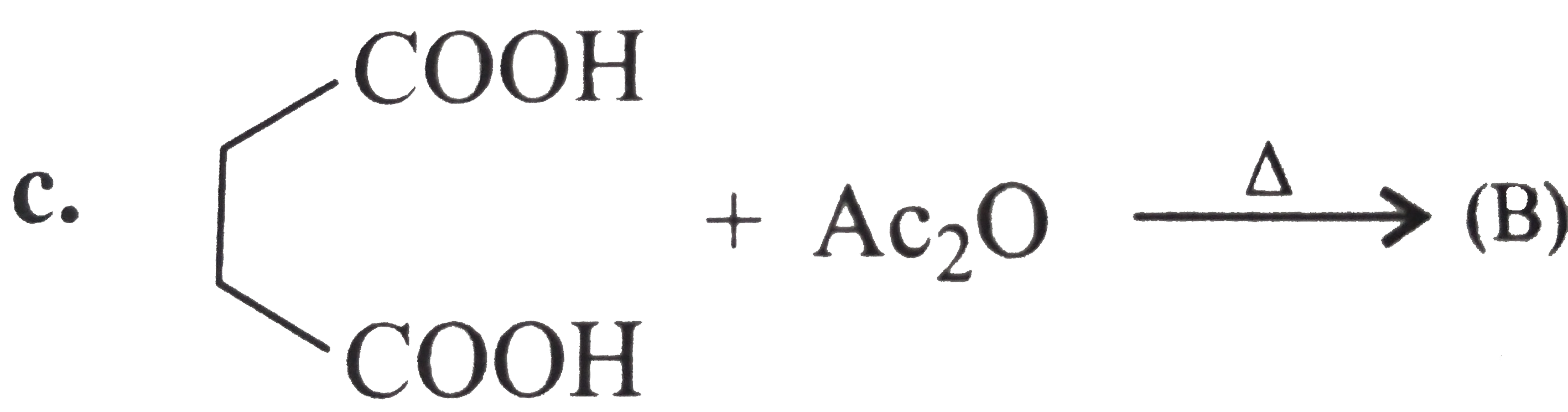
(d)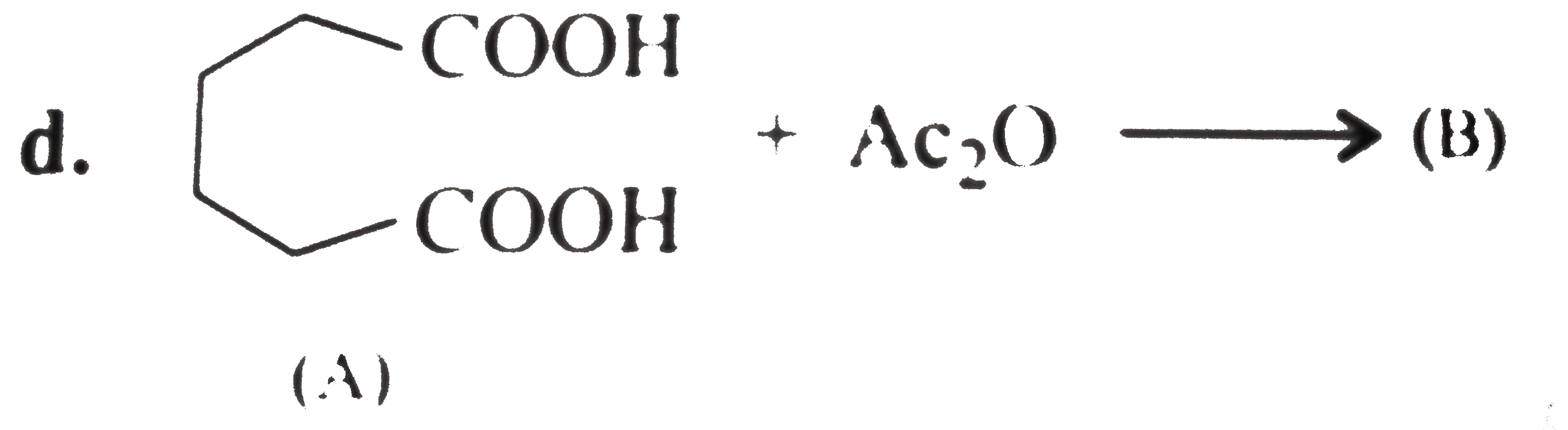
( e)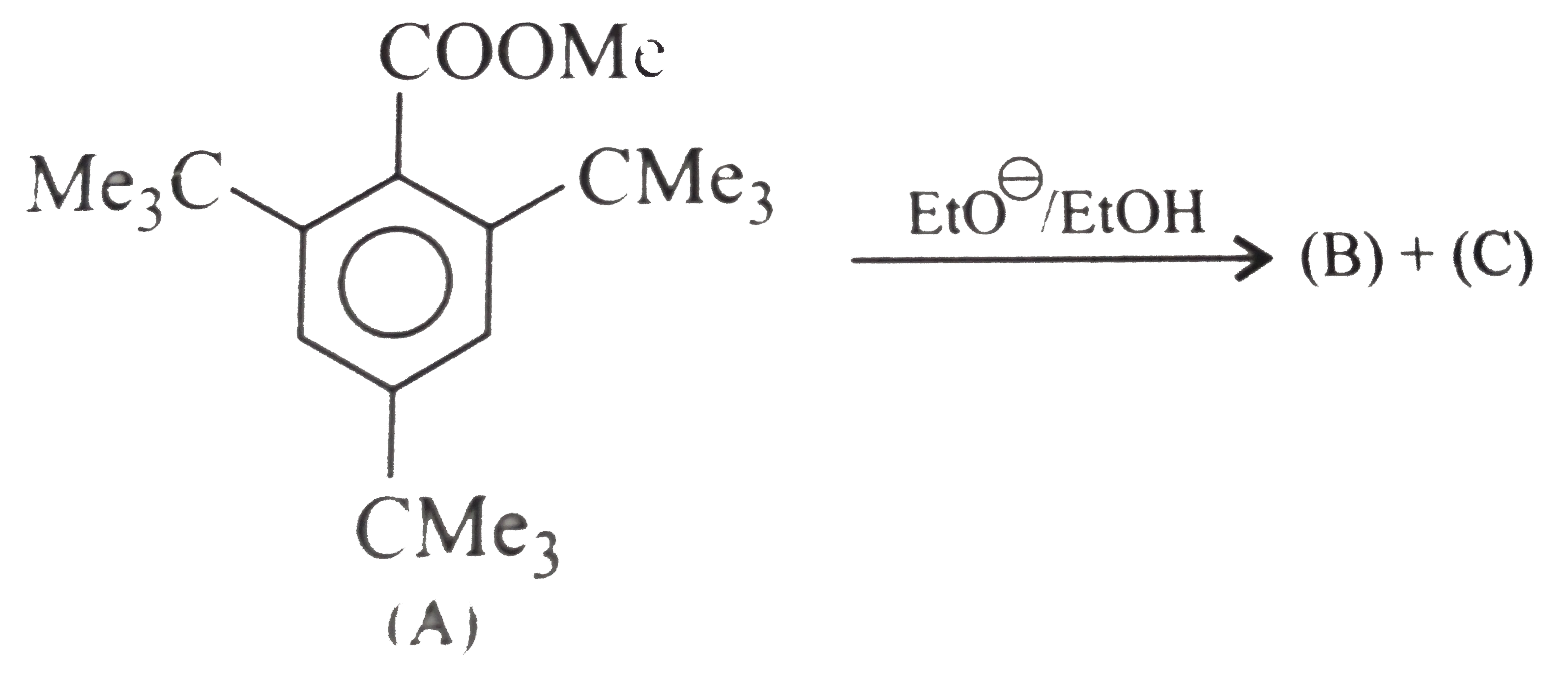
(f)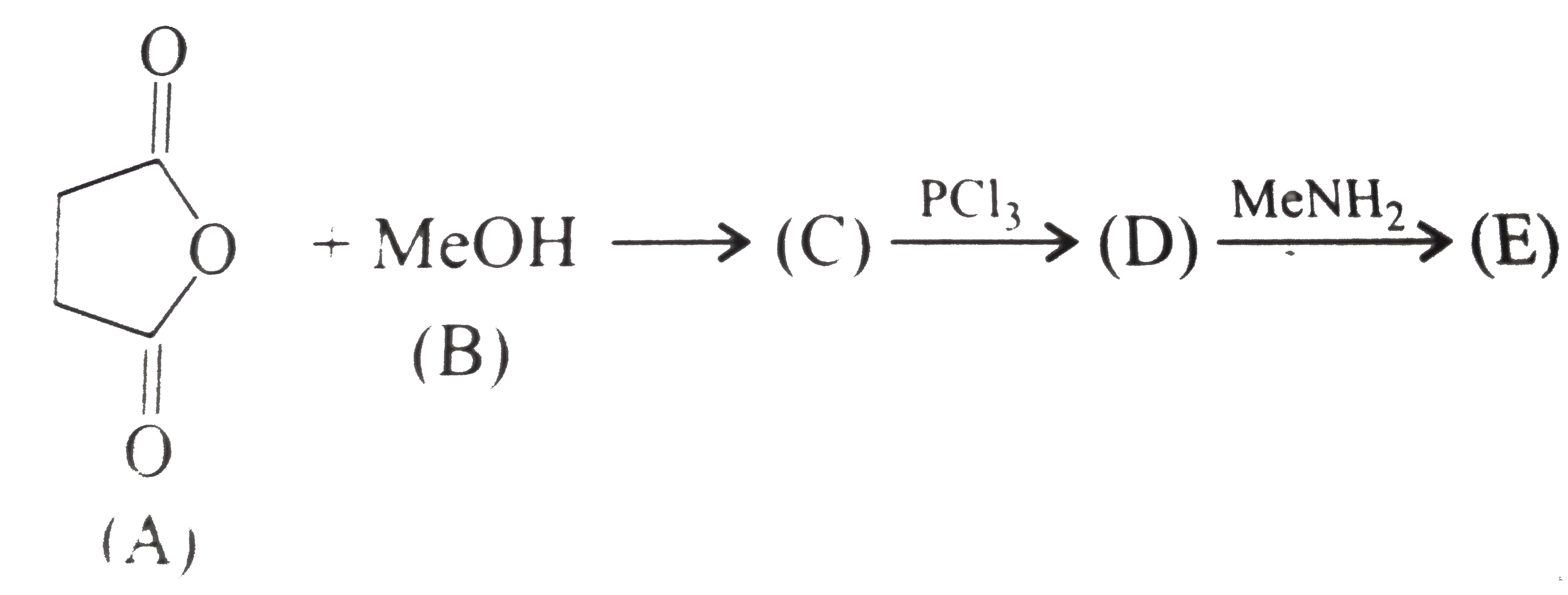
(g)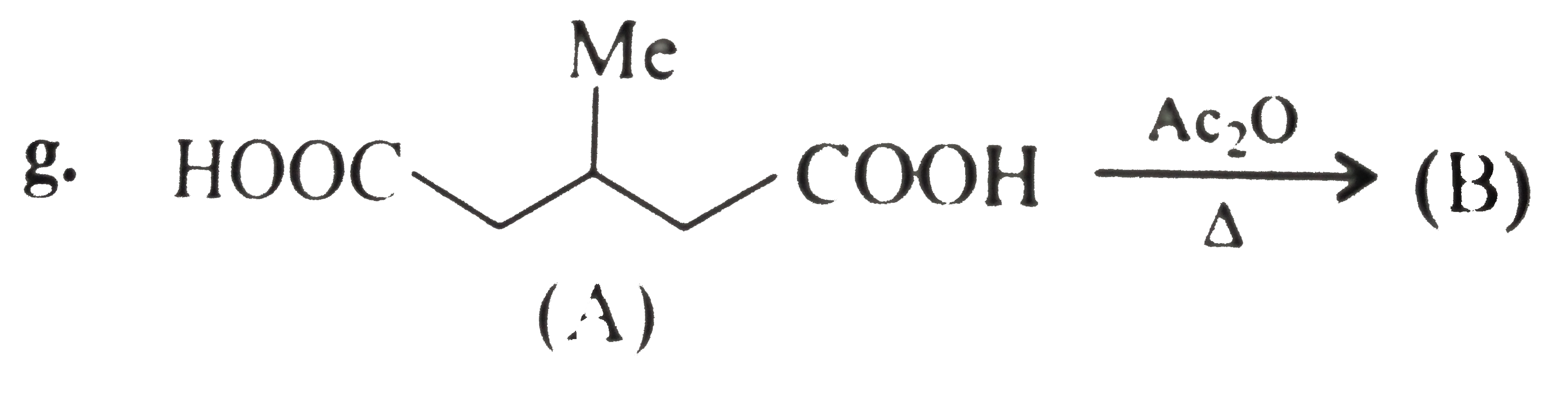 .
.
View SolutionComplete the following reactions :
(a)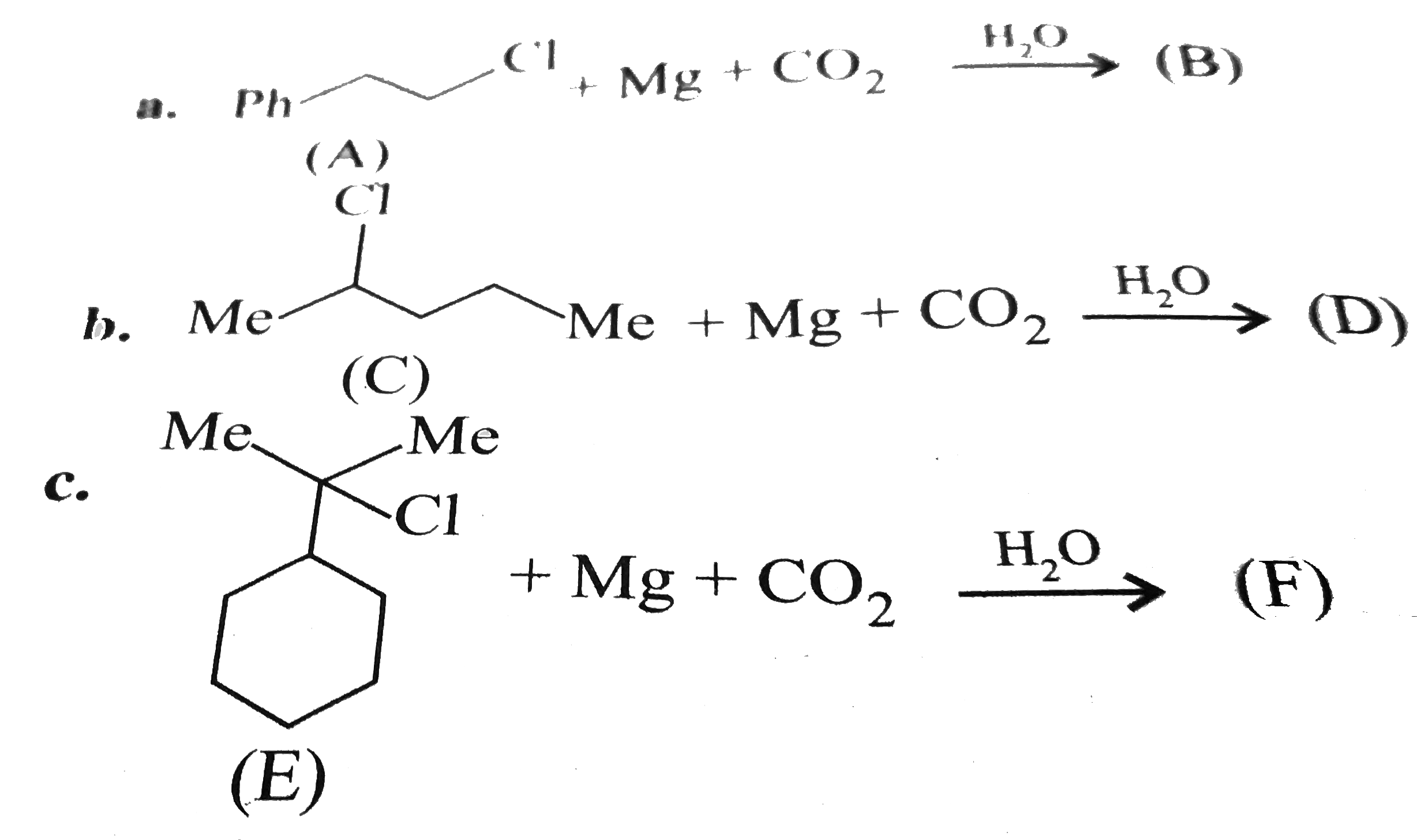
(b)
(d) PhCl(G)+Mg+CO2H2O−−→(H)
(f) trans-4-Chloro(N) methyl cyclohexane +Mg+CO2H2O−−→(O)
(g)
(h) RMgBr(U)+CO2Ether,Δ−−−−−→H2IValericacid(V).
(i) RMgBr(W)+CO2Ether,Δ−−−−−→H2OCaproicacid(X).
View SolutionGive the structure of the compounds in the following reactions
CH2=CH−CH2OHCrO3.2C5H5N−−−−−−−−→CH2Cl2[A]CH3OH−−−−→H+[B]C5H10O2KMnO4/OH−−−−−−−−−−→(Cold,dil)[C](C5H12O4)H3O+−−−→[D](C3H6O3)
View SolutionIdentify (B) and (D) in the following sequence of reactions:
H2C=CH2conc.H2SO4−−−−−−−→(A)H2O−−→Δ(B)PB3−−→(C)(D)−−→(H2C=CH2)
View Solution

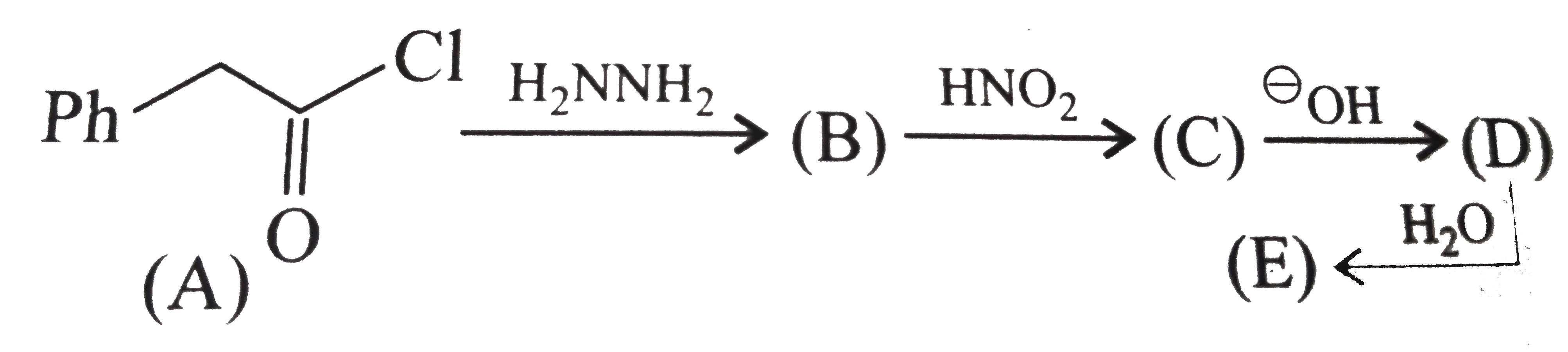
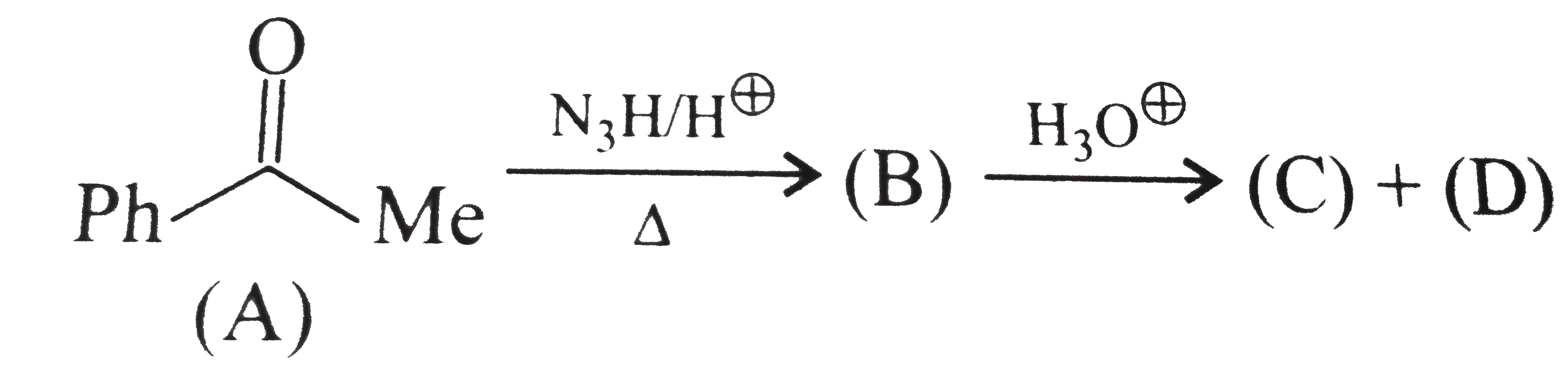
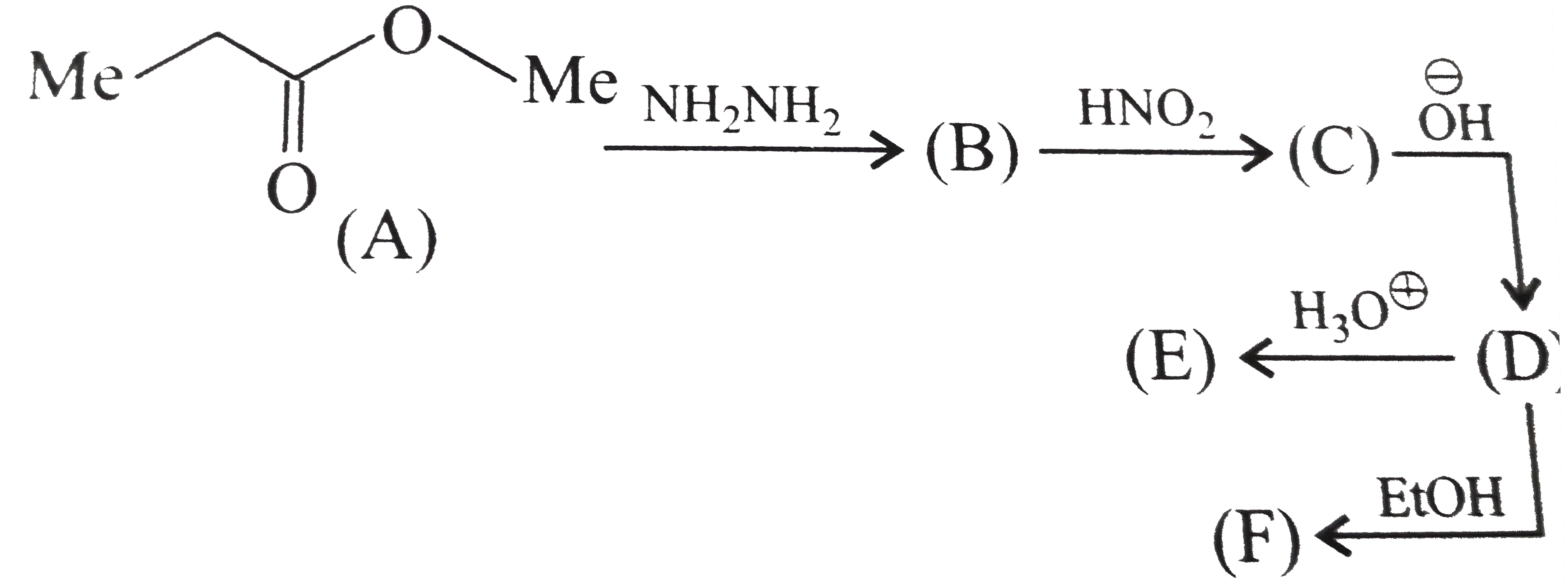
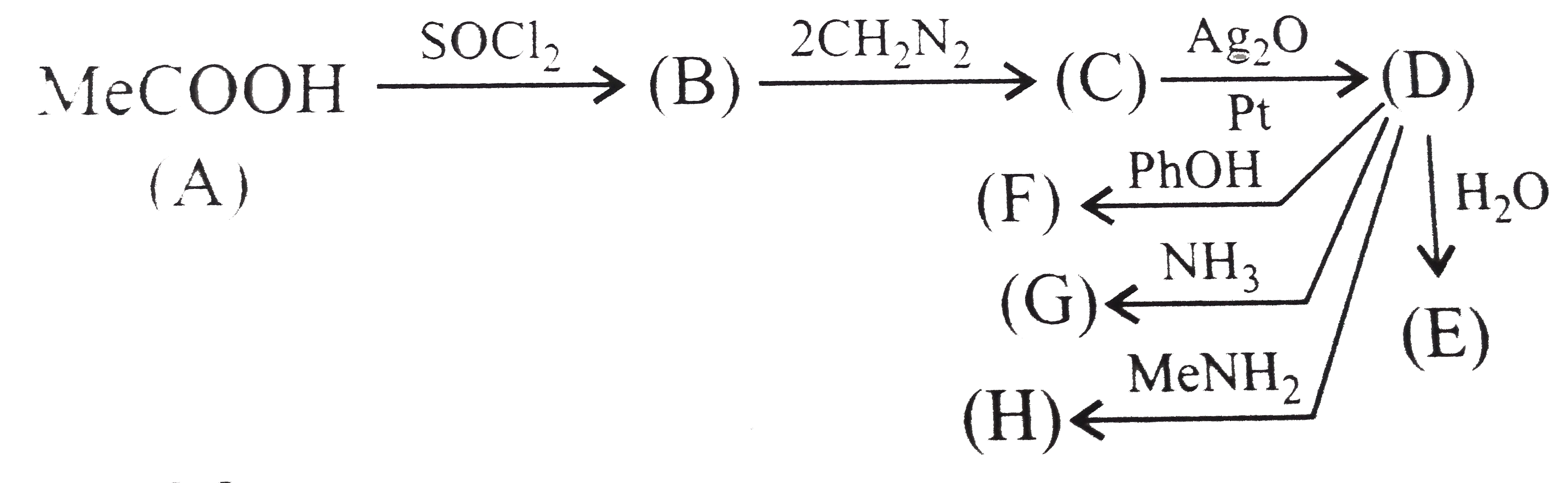
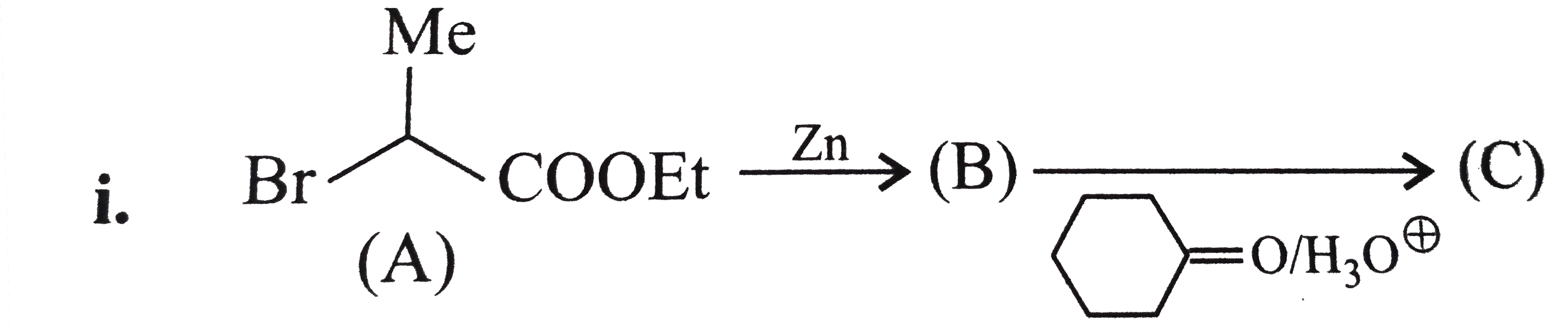
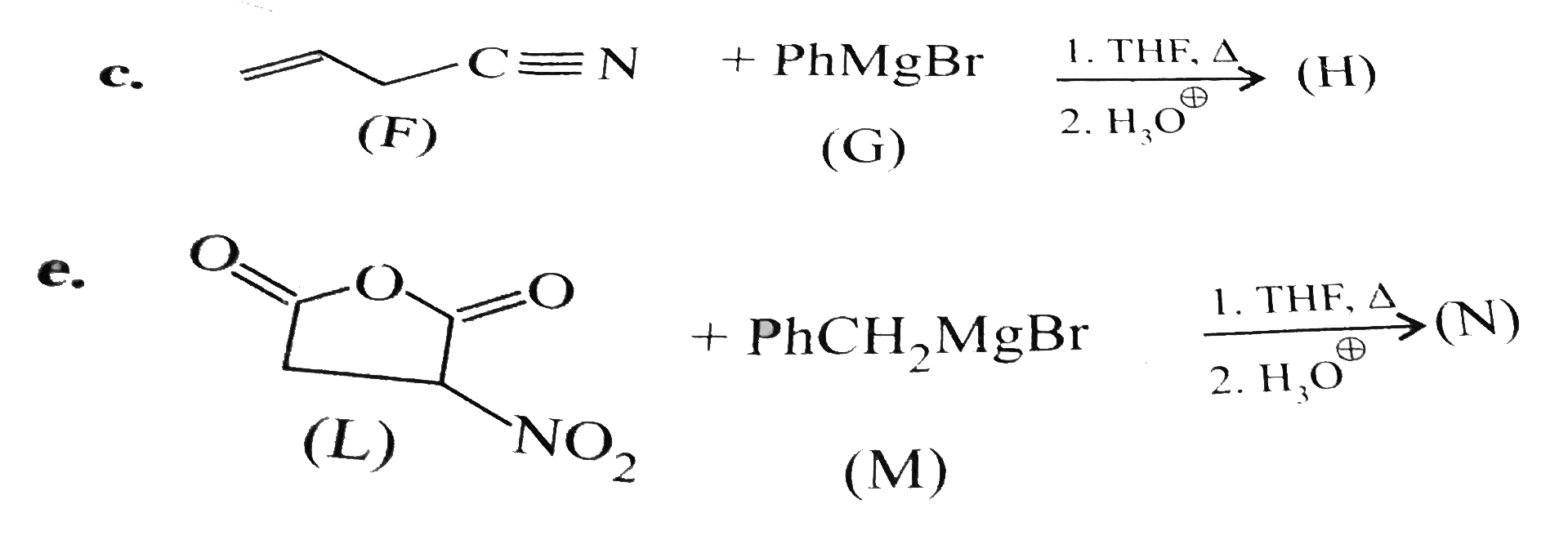
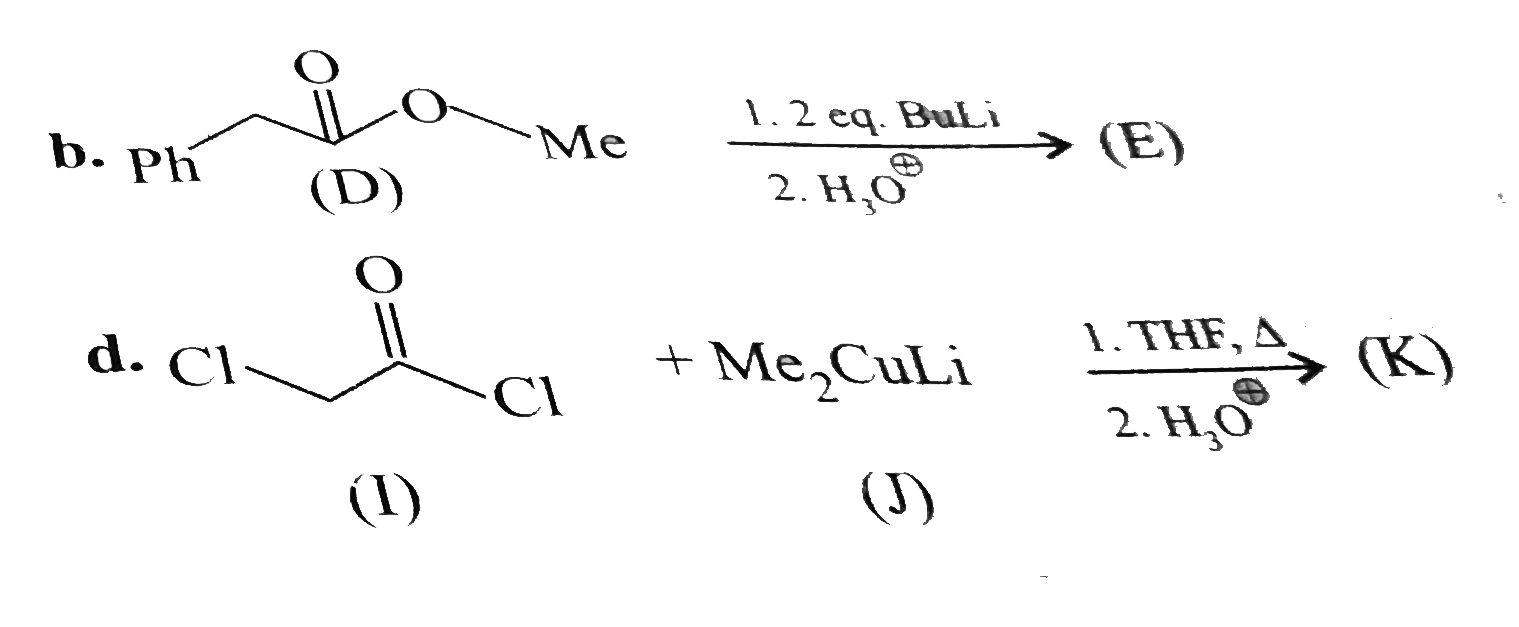

 .
.