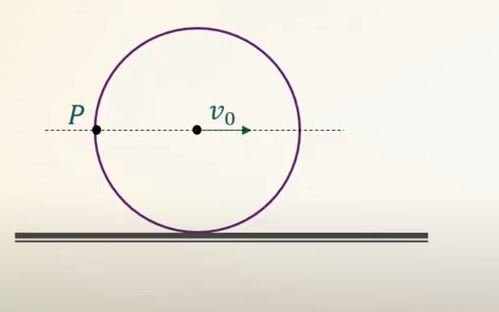
The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
√2υ0
2υ0
υ0
zero
The correct Answer is:A
In Fig.
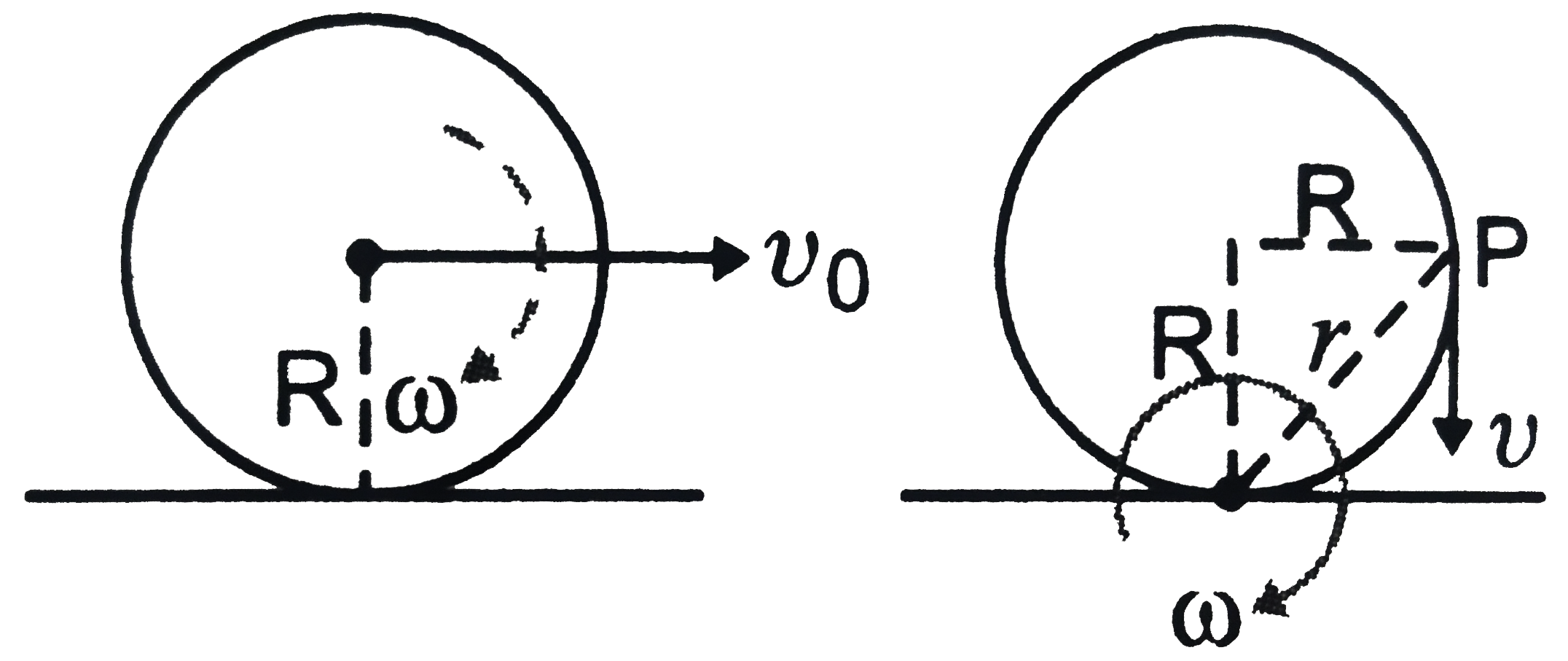
υ0=Rω
At P,υ=rω=√R2+R2(ω)
=√2Rω=√2υ0
Similar Questions
The centre of a wheel rolling on a plane surface moves with a speed v0 . A particle on the rim of the wheel at the same level as the centre will be moving at a speed √xv0 . Then the value of x is ______ .
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View Solution
Knowledge Check
The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0The centre of a wheel rolling on a plaen surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
AZeroBv0C√2v0D2v0The locus of the centre of a wheel rolling on a straight road is a ______
Aconcentric circleBstraight lineCcurve pathDparabola
The centre of the wheel rolling on a plane surface moves with velocity v0. A particle on the rim of the wheel at same level as the centre will be √xv0. Find x
View SolutionTwo thin rings of slightly different radii are joined together to make a wheel (see figure) of radius R. There is a very small smooth gap between the two ring. The wheel has a mass M and its centre of mass is at its geometrical centre. The wheel stands on a smooth surface and a small particle of mass m lies at the top (A) in the gap between the rings. The system is released and the particle begins to slide down along the gap. Assume that the ring does not lose contact with the surface.

(a) As the particle slides down from top point A to the bottom point B, in which direction does the centre of the wheel move?
(b) Find the speed of centre of the wheel when the particle just reaches the bottom point B. How much force the particle is exerting on the wheel at this instant?
(c) Find the speed of the centre of the wheel at the moment the position vector of the particle with respect to the centre of the wheel makes an angle q with the vertical. Do this calculation assuming that the particle is in contact with the inner ring at desired value of θ
View SolutionIn above question, what will be the speed of the particle on the ring which is at the same height as that of the centre?
View SolutionA wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
View SolutionConsider a wheel of a bicycle rolling on a level road at a liner speed v0 figure.

View Solution
