When a force is applied on a wire of uniform cross-sectional area 3×10−6m2 and length 4 m, the increase in length is 1mm. Energy stored in it will be (Y=2×1011N/m2)
6270 J
0.177 J
0.075 J
0.150 J
The correct Answer is:C
To find the energy stored in the wire when a force is applied, we can use the formula for elastic potential energy stored in a stretched wire:
U=12FΔL
where:
- U is the energy stored,
- F is the force applied,
- ΔL is the increase in length of the wire.
First, we need to find the force F applied to the wire using Young's modulus Y:
Y=F/AΔL/L
Rearranging this, we can express the force F as:
F=Y⋅A⋅ΔLL
Step 1: Substitute the given values into the formula for force
Given:
- Y=2×1011N/m2
- A=3×10−6m2
- ΔL=1mm=1×10−3m
- L=4m
Substituting these values into the equation for force:
F=2×1011N/m2⋅3×10−6m2⋅1×10−3m4m
Step 2: Calculate the force F
Calculating the numerator:
3×10−6m2⋅1×10−3m=3×10−9m3
Now substituting this back into the force equation:
F=2×1011⋅3×10−94
Calculating 3×10−94:
3×10−94=0.75×10−9=7.5×10−10
Now substituting this into the force equation:
F=2×1011⋅7.5×10−10=1.5×102N=150N
Step 3: Calculate the energy stored U
Now we can calculate the energy stored using the force we just calculated:
U=12FΔL
Substituting the values of F and ΔL:
U=12⋅150N⋅1×10−3m
Calculating this:
U=12⋅150⋅1×10−3=75×10−3=0.075J
Final Answer
The energy stored in the wire is 0.075J.
---
- U is the energy stored,
- F is the force applied,
- ΔL is the increase in length of the wire.
- Y=2×1011N/m2
- A=3×10−6m2
- ΔL=1mm=1×10−3m
- L=4m
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Surface Tension And Surface Energy
29 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Pressure Difference And Capillarity
23 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
(a) A wire 4 m long and 0.3mm in diameter is stretched by a force of 100 N. If extension in the wire is 0.3 mm, calculate the potential energy stored in the wire.
(b) Find the work done is stretching a wire of cross-section 1mm2 and length 2 m through 0.1 mm. Young's modulus for the material of wire is 2.0×1011Nm−2.
View SolutionA steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
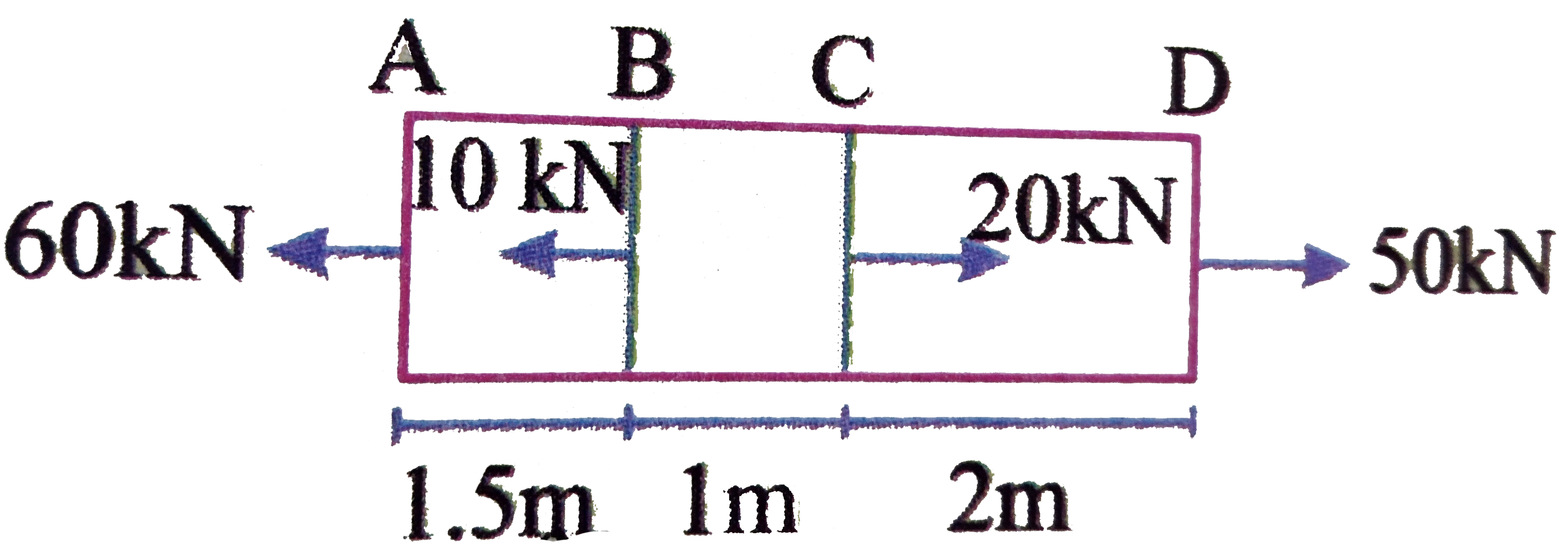
View Solution
Knowledge Check
When a force is applied on a wire of uniform cross-sectional are 3×10−6m2 and length 4 m, the increase in length is 1 mm. Energy stored in it will be (Given, Y=2×1011Nm−2)
A6250 JB0.177 JC0.075 JD0.150 JWhat is the energy stored per unit volume in a copper wire of uniform cross section and length 1.5 m, when it is stretched to a length of 1.51 m by a stress of 3×102N/m2 ?
A0.25J/m3B0.5J/m3C0.75J/m3D1J/m3There is some change in length when a 33000N tensile force is applied on a steel rod of area of cross-section 10−3m2. The change of elongation of the steel rod when heated is
(Y=3×1011N/m2,α=1.1×10−5/∘C)A20∘CB15∘CC10∘CD0∘C
A stell wire of 1m long 1mm2 cross section area is hang from rigid end. The length of 1kg is hung from it then change in length will be (given Y=2×1011N/m2)
View SolutionA brass rod of cross-sectional area 1cm2 and length 0.2 m is compressed lengthwise by a weight of 5 kg. if young's modulus of elasticity of brass is 1×1011N/m2 and g=10m/sec2 then increase in the energy of the rod will be
View SolutionThe resistance of a wire of length 330m and cross-section area 1.0mm2 made of material of resistivity 1.0×10−7Ωm is:
View SolutionA brass rod of cross-sectional area 1cm2 and length 0.2cm is compressed lengthwise by a weight of 5kg. If Young's modulus of elasticity of brass is 1×1011N/m2 and g=10m/sec2, then increase in the energy of the rod will be
View SolutionA wire of area of cross section 1×10−6m2 and length 2 m is stretched through 0.1×10−3m. If the Young's modulus of a wire is 2×1011N/m2, then the work done to stretch the wire will be
View Solution
