Two wires shown in figure are made of the same material which has a breaking stress of 8×108Nm2. The area of cross- section of the upper wire is 0.006cm2 and that of the lower wire is 0.003cm2. The mass m1=10kg,m2=20kg and the hanger is light . Find the maximum load that can be put on the hanger without breaking a wire. Which wire will break first if the load is increased ? ( Take g=10m/s2)

14 kg
1.4 kg
1.2 kg
12 kg
The correct Answer is:A
Let load put on the hanger is F then stress in lower wire
S1=m1g+F0.003×10−4
Let S1=8×108Nm2, then
8×108=10×10+F3×10−7⇒F=140N
Let stress developed in upper wire is S2, then S2=(m1+m2)g+F0.006×10−4
Let S2=8×109Nm2
8×108=(10+20)10+f6×10−7⇒F=180N
We have to select the lower value of F. Hence maximum load that can be suspended is 140g=14kg.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus
29 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Elasticity And Work Done In Stretching A Wire
25 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
The two wires shown in figure are made of the same material which has a breaking stress of 8×108Nm−2. The area of cross section of the upper wire is 0.006 cm^2 and that of the lower wire is 0.003 cm^2. The mass m−1=10kg,m2=20kg and teh hanger is light. a. Fidn the maximum load that casn be put on the hanger without breaking a wire. Which wire will break first if the load is increased? b. Repeat the above part m1=10kgandm2=36kg.

View SolutionWires W1 and W2 are made of same material having the breaking stress of 1.25×109N/m2.W1andW2 have cross-sectional area of 8×10−7m2and4×10−7m2, respectively. Masses of 20 kg and 10 kg hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is kg. (Use g=10m/s2)
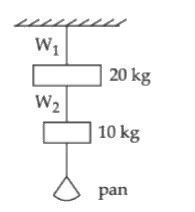
View Solution
Knowledge Check
The density of the material of a wire used in sonometer is 75×10−2kg/m3. If the stress on the wire is 3.0×104N/m2, the speed of transverse wave in the wire will be
A100 m/sB200 m/sC300 m/sD400 m/sA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
A8rad/secB4rad/secC2rad/secD1rad/secA bob of mass 10kg is attached to a wire 0.3m long. Its breaking stress is 4.8×107N/m2. Then area of cross-section of the wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
A8rad/sB4rad/sC2rad/sD1rad/s
A wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionA body of mass 10 kg is attached to a wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross-section of wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
View SolutionThe density of the material of a wire used in sonometer is 7.5×103 kg//m^(3)Ifthesestressonthewireis3.0×108N/m3 the speed of transverse wave in the wire will be -
View SolutionThe area of cross section of a steel wire (Y=2.0×1011N/m2) is 0.1cm2. The force required to double is length will be
View SolutionTwo wires are made of the same material and have the same volume. However wire 1 has cross-section area A and wire 2 has cross-section area 3A. If length of wire 1 increased by
View Solution
