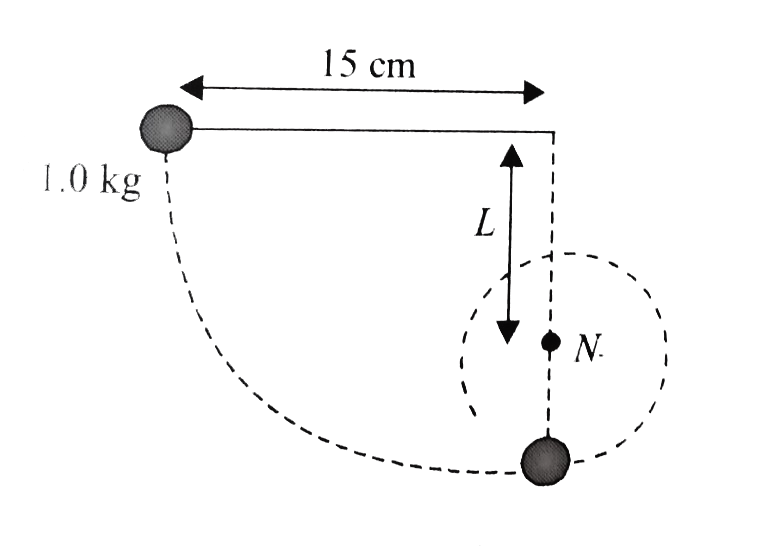
A ball weighing 1.0 kg is tied to a string 15 cm long initially the ball is held in position such that the string is horizontal. The ball is now released. A nail N is situated vertically below the support at a distance L. The minimum value of L such that the string will be would round the nail is.
15 cm
4 cm
9 cm
None of these
Velocity of bob at C should be √5gR
√5g(R−L)=√2gR
5(R−L)=2R
3R=5L
L=35R=35×15=9cm
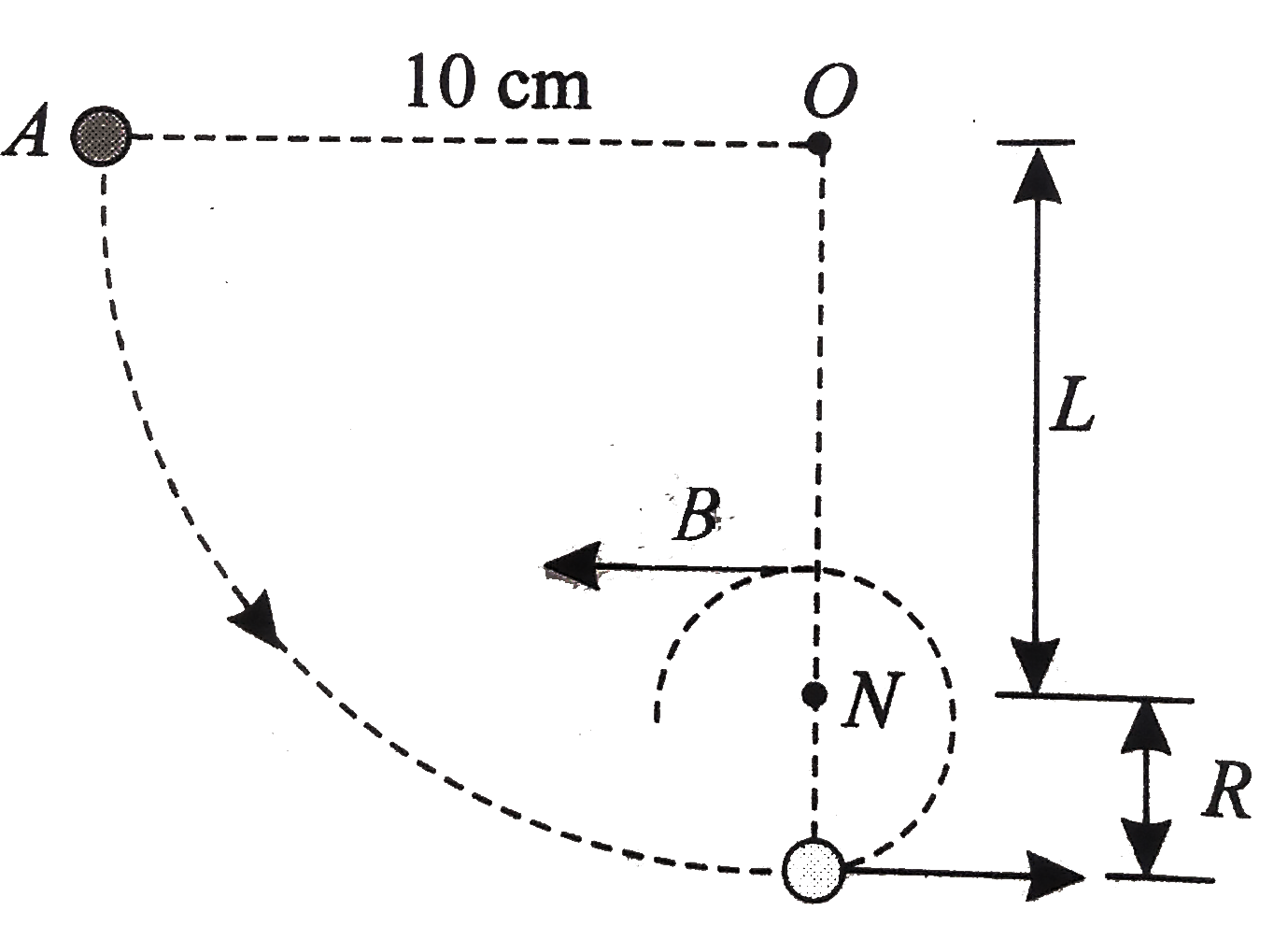
Similar Questions
A ball of mass 100 g is suspended by a string 40cm long. Keeping the string taut, the ball describes a horizontal circle of radius 10 cm. Find the angular speed.
View SolutionA ball is attached to a string of length L. The ball is released when the string is horizontal. The ball collides with wall and e=2/√5. After how many minimum number of collisions , the amplitude of oscillation becomes less than 60∘.

View SolutionA ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
View Solution
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.
View SolutionA ball of mass 0.1kg is suspended by a string 30cm long Keeping the string always taut the ball describe a horizontal circle of radius 15cm Calculate the angular speed of the ball .
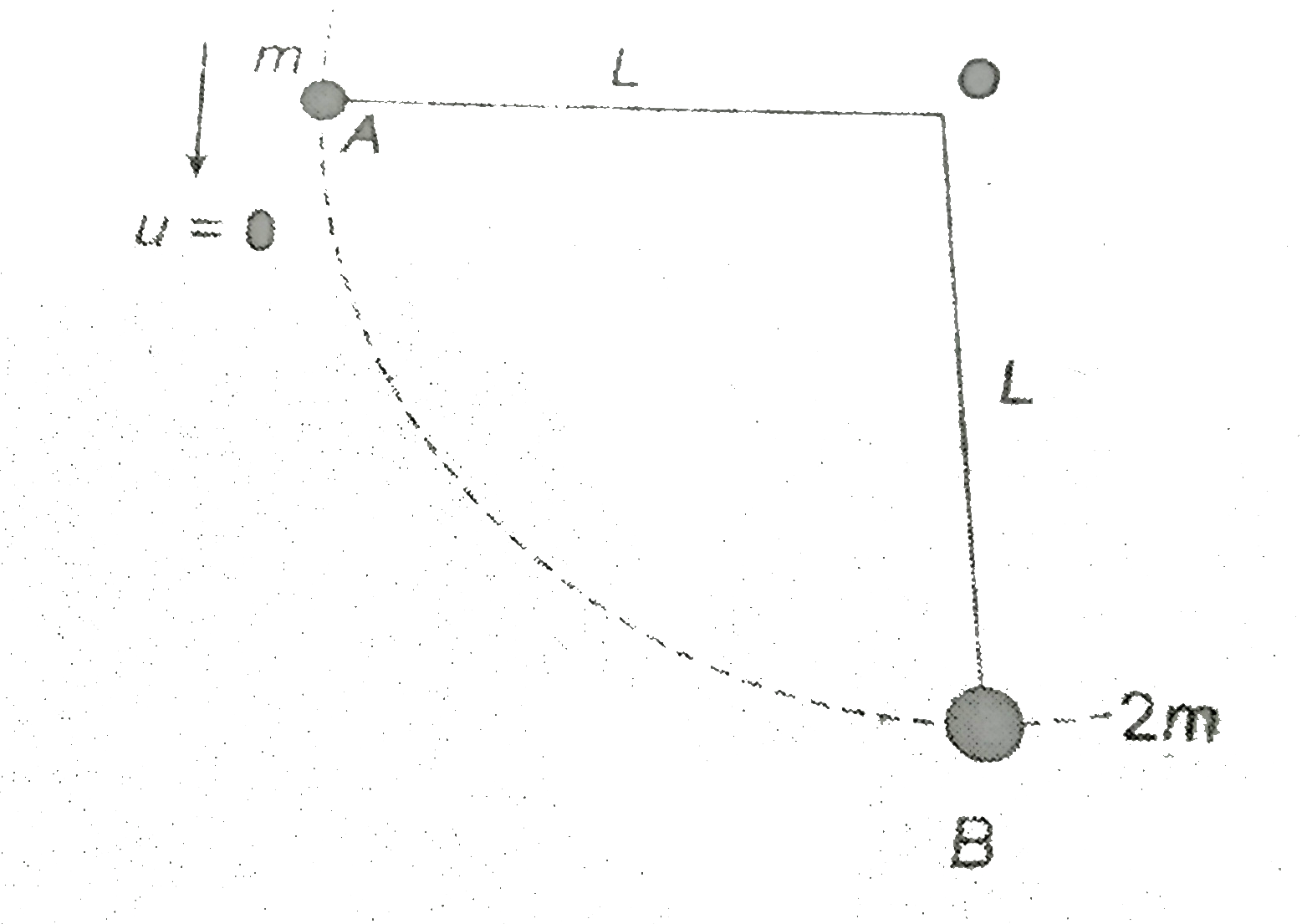
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
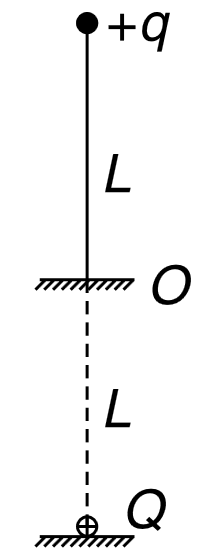
View SolutionA particle of mass m and charge q is attached to a light insulating thread of length L. The other end of the thread is secured at point O. Exactly below point O, there is a small ball having charge Q fixed on an insulating horizontal surface. The particle remains in equilibrium vertically above the ball with the string taut. Distance of the ball from point O is L. Find the minimum value of Q for which the particle will be in a stable equilibrium for any gentle horizontal push given to it.
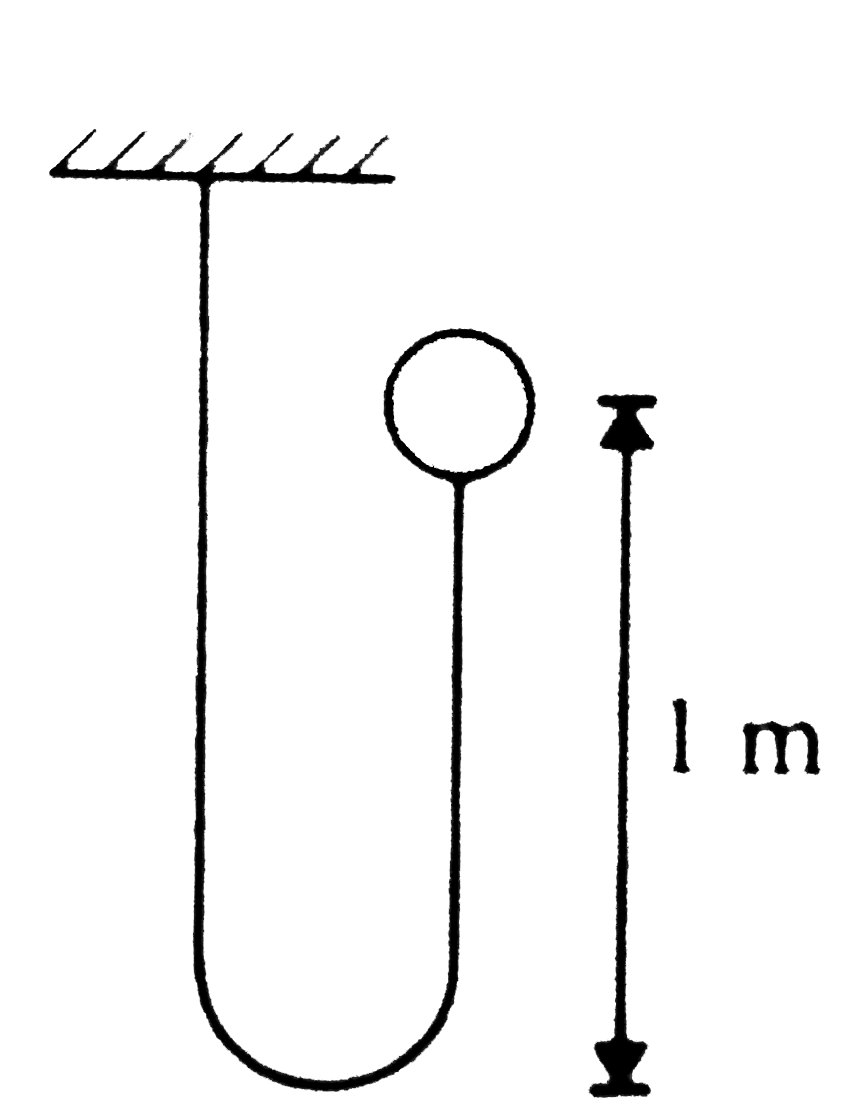
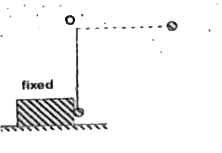
View SolutionA steel ball is suspended by a light in extensible string of length l from a fixed point O. When the ball is in equilibrium it just touches a vertical wall as shown in the figure. The ball is first taken aside such that string becomes horizontal and then released from rest. If coefficient of restitution is e, then find the maximum deflection of the string after nth collision.

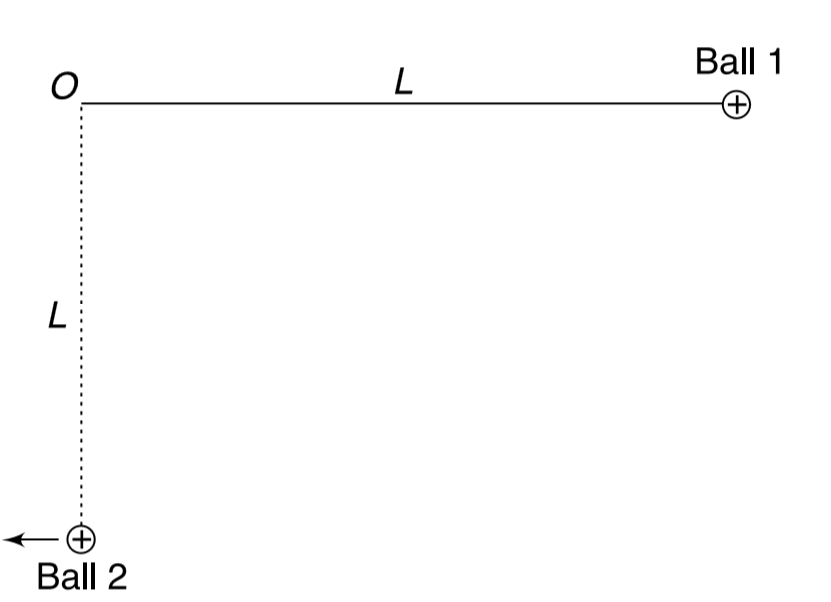
View SolutionA small positively charged ball of mass m is suspended by an insulating thread of length L. This ball remains in equilibrium with string horizontal when another small charged ball is placed exactly at a distance L below the point of suspension of the first ball. The second ball is slowly moved away from the first ball to a far away point. (The second ball is moved horizontally so that the first ball does not accelerate). As a result the first ball lowers down to the original position of the second ball and the string become vertical. Find the work done by the external agent in removing the second ball.
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
View Solution
