The spring block system lies on a smooth horizontal surface. The free endof the spring is being pulled towards right with constant speed v0=2m/s. At t=0sec, the spring of constant k=100N/cm is unsttretched and the block has a speed 1m/s to left. The maximum extension of the spring is.
 .
.
2 cm
4 cm
6 cm
8 cm
The correct Answer is:C
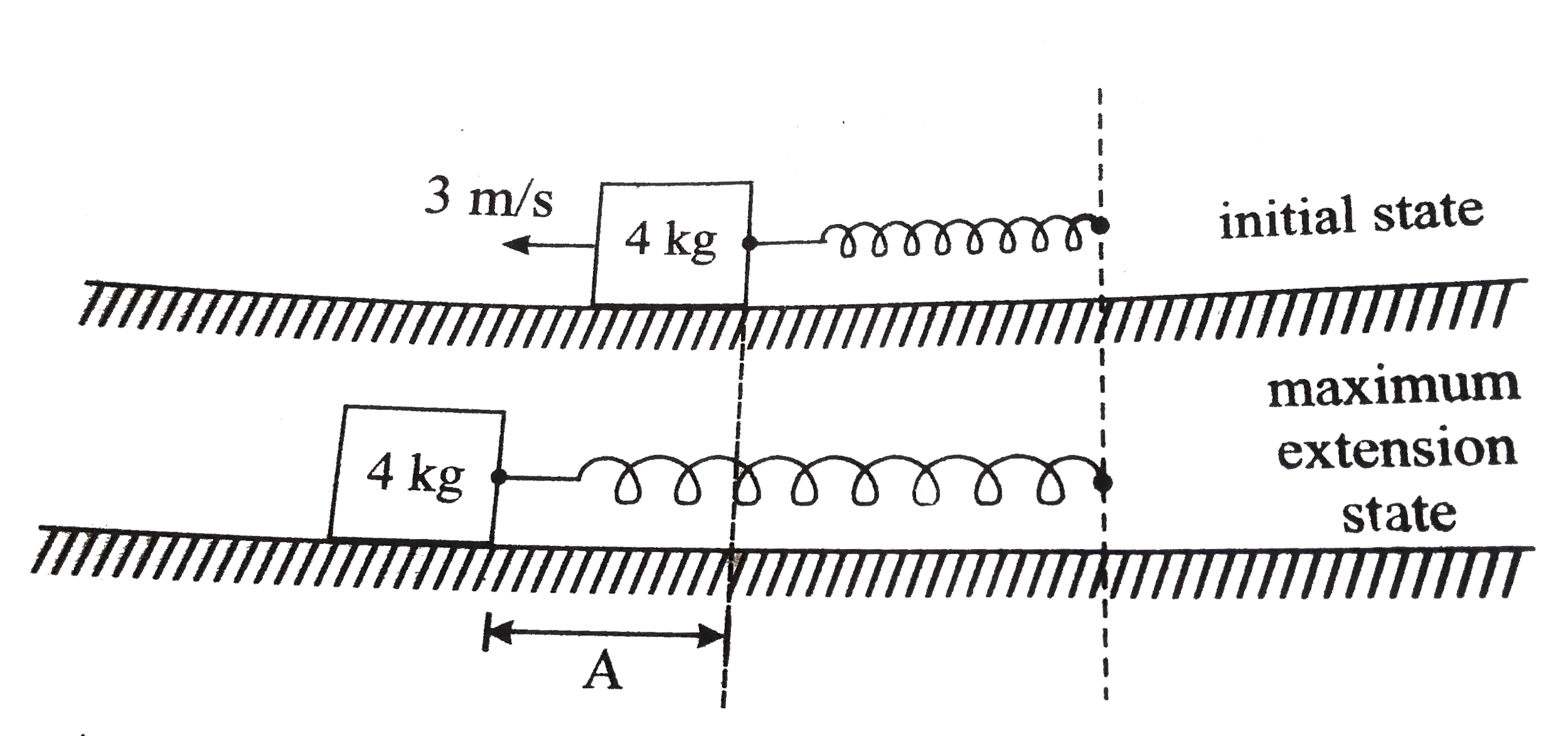
In the frame (inertial w.r.t. earth) of free end of spring the initial velocity of block is 3ms to left and the spring unstretched. Applying conservation of energy between initial and maximum extension state.
12mv2=12kA2
or A=√mkv=√41000×3=6cm
Similar Questions
A block of mass 2 kg is connect to an ideal spring and the system is placed on a smooth horizontal surface. The spring is pulled to move the block and at an instant the speed of end A of the spring and speed of the block were measured to be 6 m/s and 3 m/s respectively. At this moment the potential energy stored in the spring is increasing at a rate of 15 J/s. Find the acceleration of the block at this instant.

View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
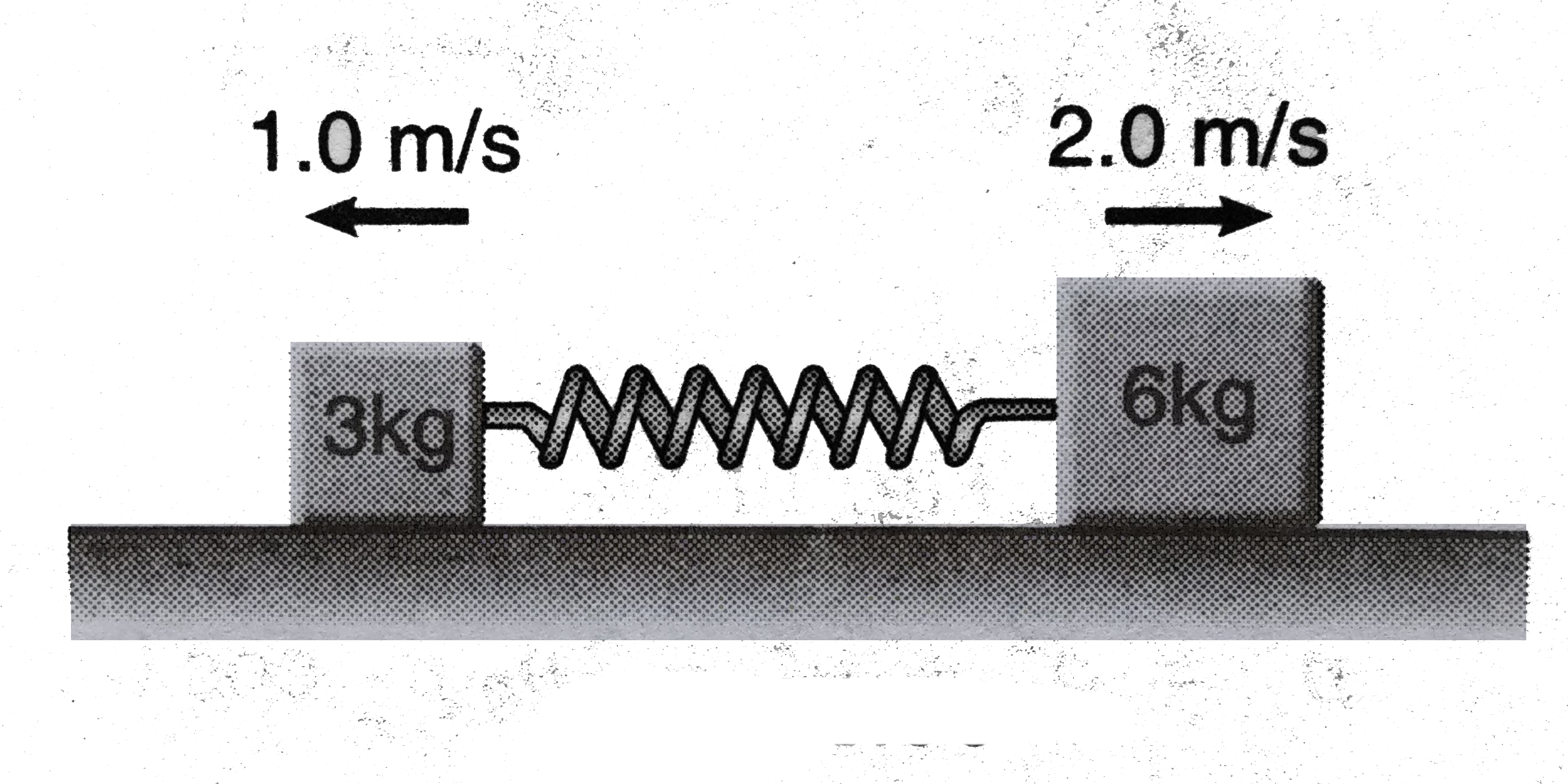
View Solution
Knowledge Check
A block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
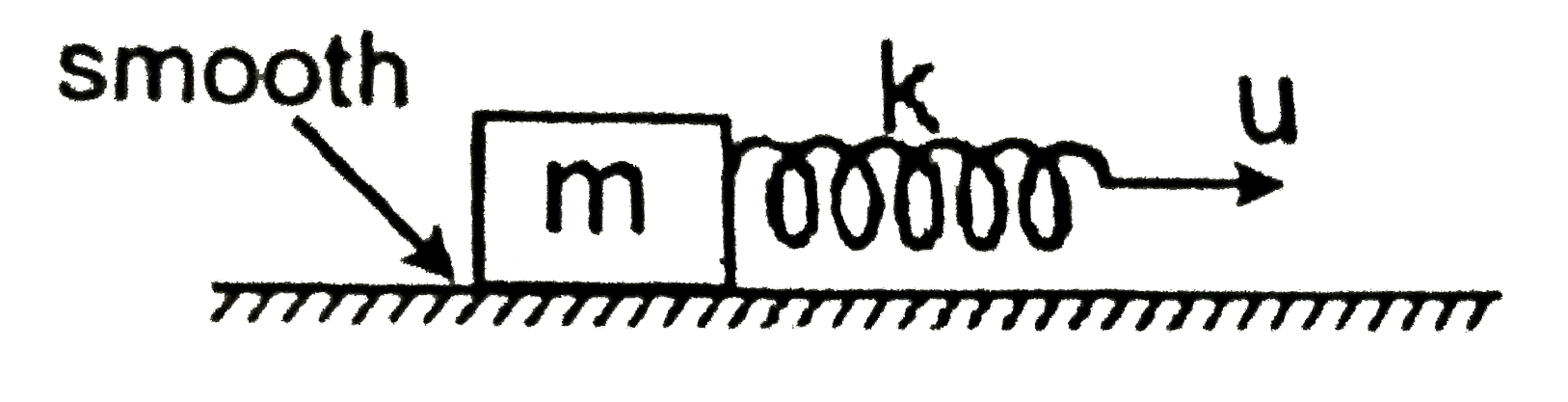 A12mu2Bmu2C2mu2D4mu2
A12mu2Bmu2C2mu2D4mu2A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvkIn spring constant of the spring is 100 N/m Extension produced in the spring is:
(g=10m/s2)
 A10 cmB20 cmC30 cmD40 cm
A10 cmB20 cmC30 cmD40 cm
A spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
View SolutionA spring has force constant k=200N/m and its one end is fixed. There is a block of mass 2 kg attached to its other end and the system lies on a smooth horizontal table. The block is pulled so that the extension in the spring becomes 0.05 m. At this position the block is projected with a speed of 1m/s in the direction of increasing extension of the spring. Consider time t = 0 at the moment the block is projected and find
(a) the extension (or compression) in the spring as a function of time.
(b) the maximum extension in the spring and the time at which it occurs for the first time.
(c) the time after which the speed of the block becomes maximum for the first time. Given: sin−1(0.446)=0.46 radian
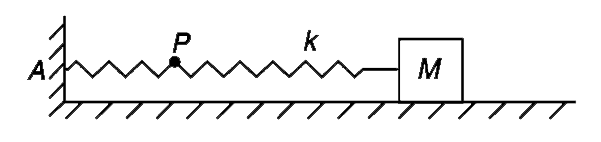
View SolutionA block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
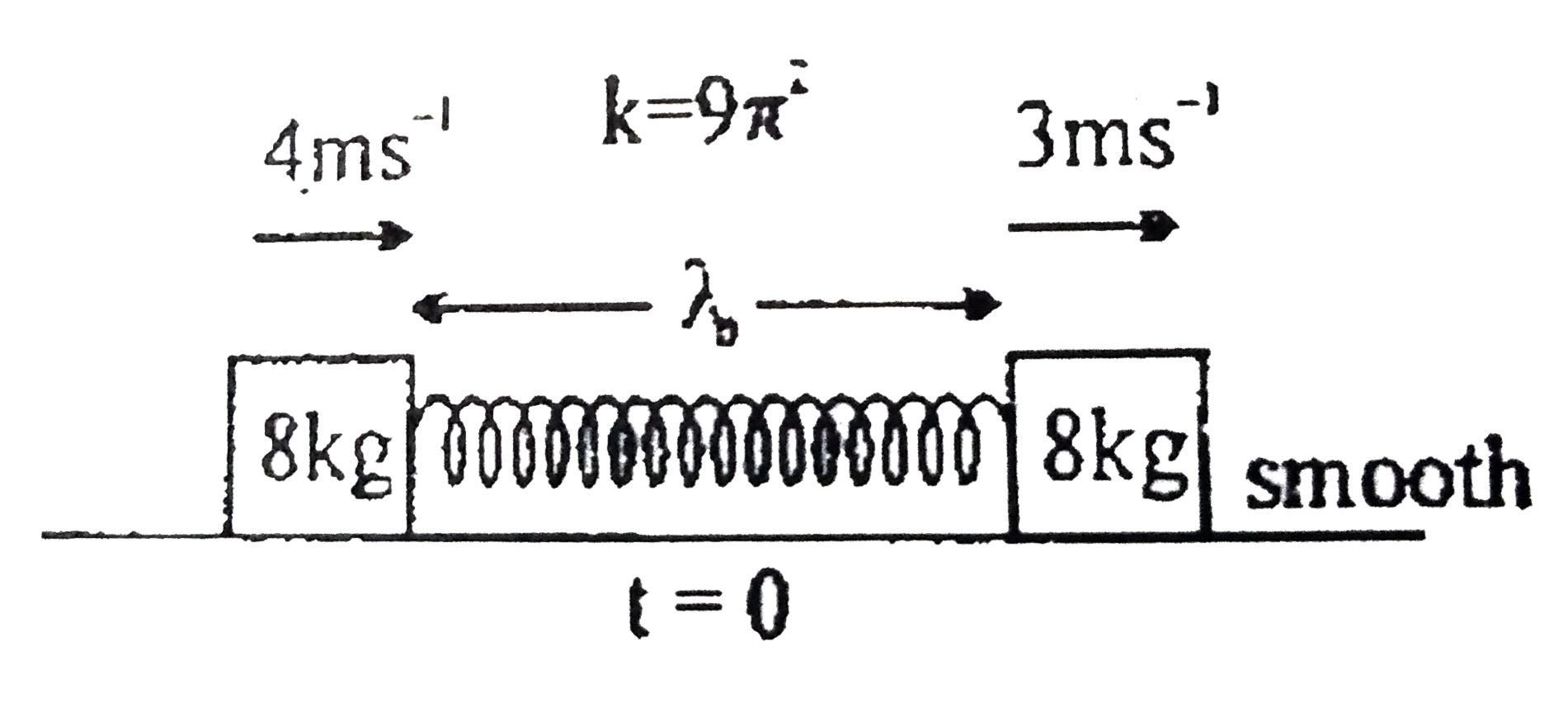
View SolutionTwo block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l0 is the natural length of spring.
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
