A ring of mass m can slide over a smooth vertical rod as shown in figure. The ring is connected to a spring of force constant k=4mg/R, where 2R is the natural length of the spring . The other end of spring is fixed to the ground at a horizontal distance 2R from base of the rod . If the mass is released at a height 1.5J then the velocity of the ring as it reaches the ground is

2√gR
√gR
√gR2
3√gR2
The correct Answer is:A
Let v be velocity of the ring as it reaches the ground. From work energy theorem,
Wgravity+Wspr∈g=△K
⇒mg(3R2)+12kx2=12mv2
⇒3mgR2+mgR2=12mv2
⇒v=2√gR
Similar Questions

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA ring of mass m=10kg can slide through a vertical rod with friction. It is connected with a spring of force constant k=100Nm−1. The relaxed length of spring is 4m. The ring is displaced 3m as shown in the figure and released. Find velocity of ring when spring becomes horizontal.
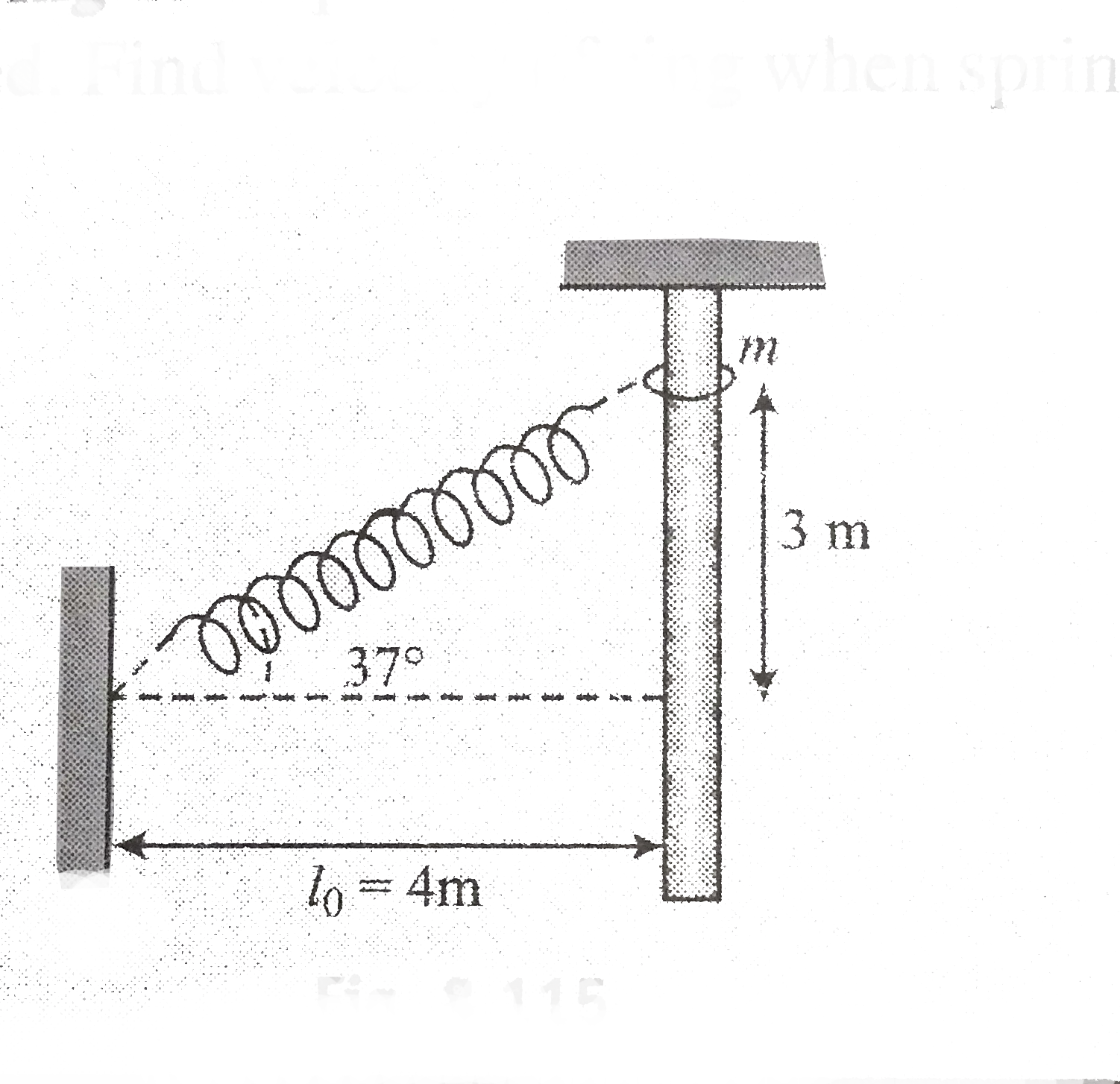
View Solution
Knowledge Check
A ring of mass m can slide over a smooth vertical rod. The ring is connected to a spring of force constant K=4mgR where 2R is the natural length of the spring. The other end spring is fixed to the ground at a horizontal distance 2R from the base of the rod. the mass is released at a height of 1.5 R from ground.
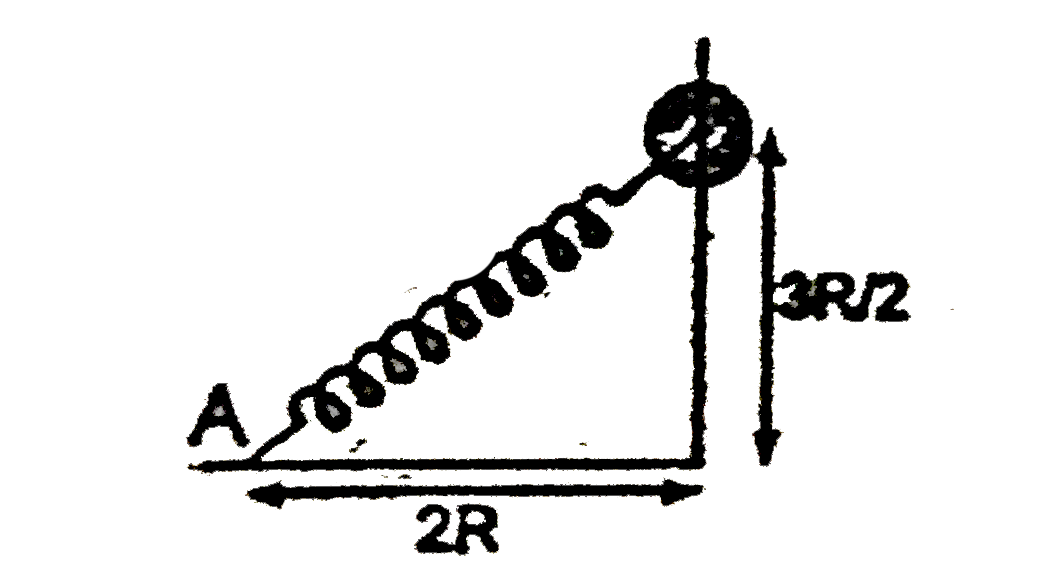 Awork done by the spring will be mgR2Bwork done by the spring will be 9mgRCthe velocity of the ring when it reaches the ground will be √gRDthe velocity of the ring when it reaches the ground will be 2√gR
Awork done by the spring will be mgR2Bwork done by the spring will be 9mgRCthe velocity of the ring when it reaches the ground will be √gRDthe velocity of the ring when it reaches the ground will be 2√gRA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
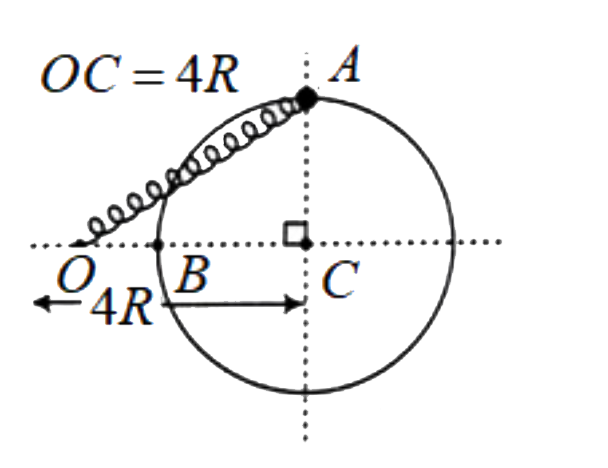 A252kR2B92kR2C8kR2D12KR2
A252kR2B92kR2C8kR2D12KR2A bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :
 A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
A(mg−mω2L)tanθmω2+kBmgtanθ+mω2Lmω2−kCmgtanθ+mω2LkDgtanθ−ω2Lω2−k/m
A bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View SolutionA block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
View SolutionA smooth ring A of mass 4 kg can slide on a fixed smooth horizontal rod. A string tied to the ring passes over a fixed pulley and carries a block B of mass 2 kg as shown in the figure. At the initial instant, the string attached to the ring makes an angle 60° with the horizontal rod. If the system is released from rest, the initial acceleration of the ring is?
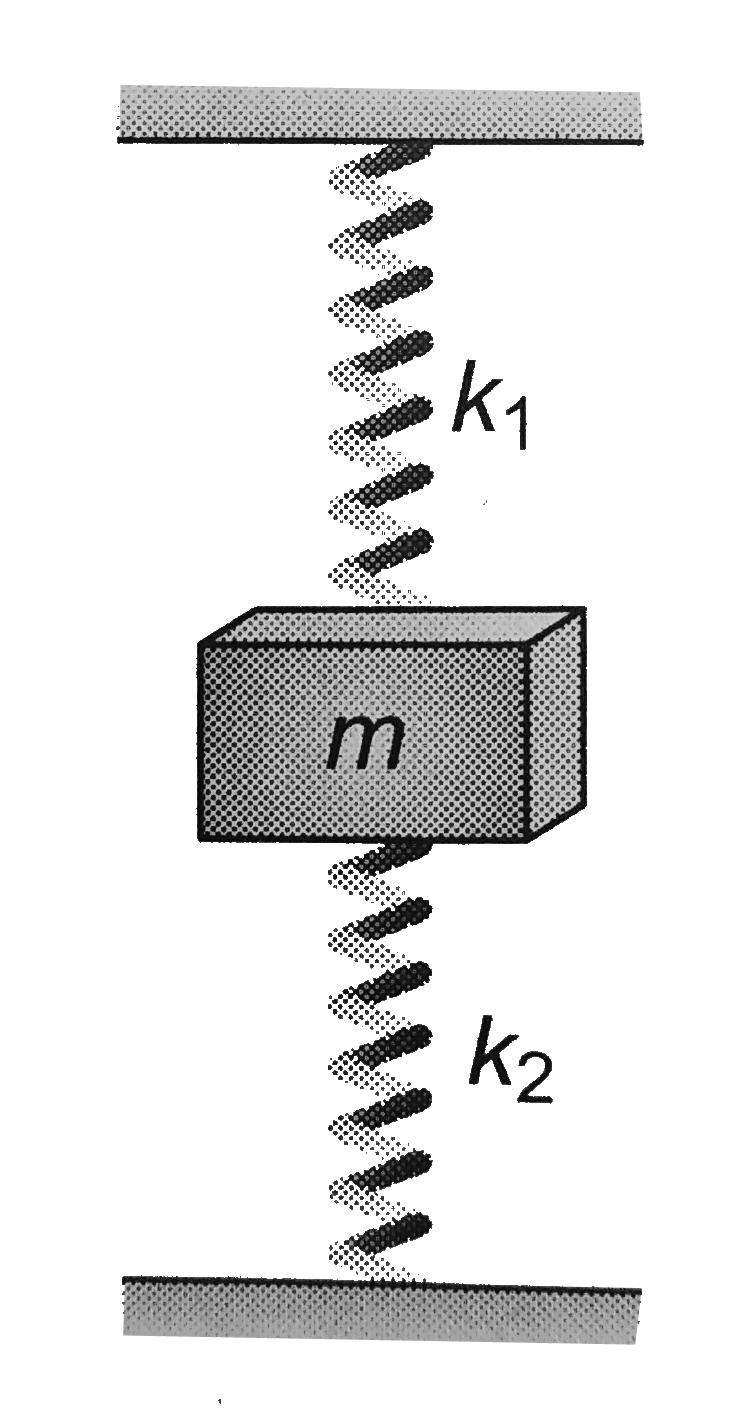
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
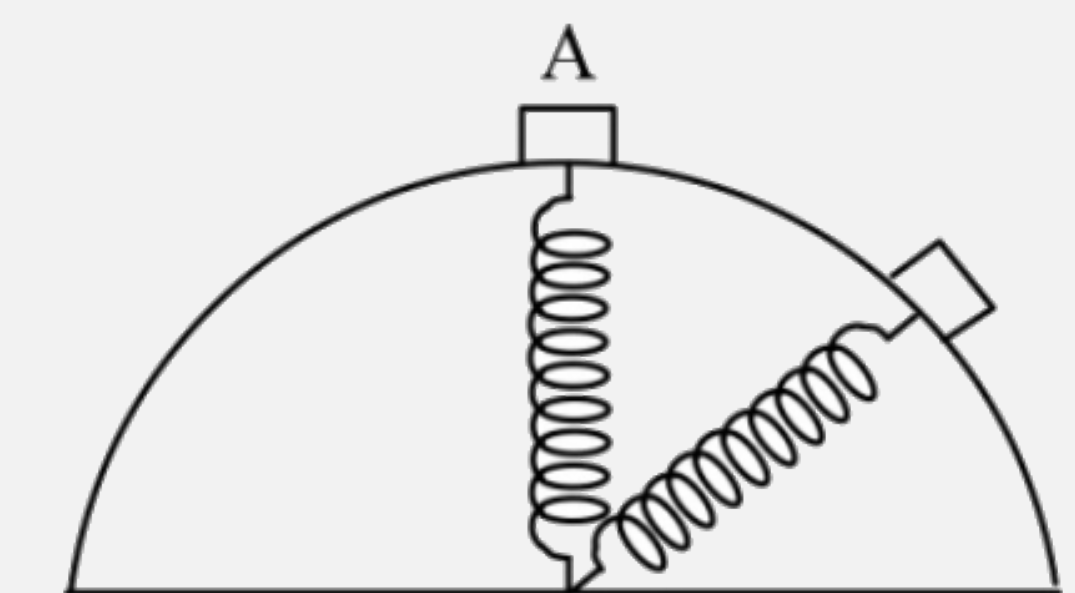
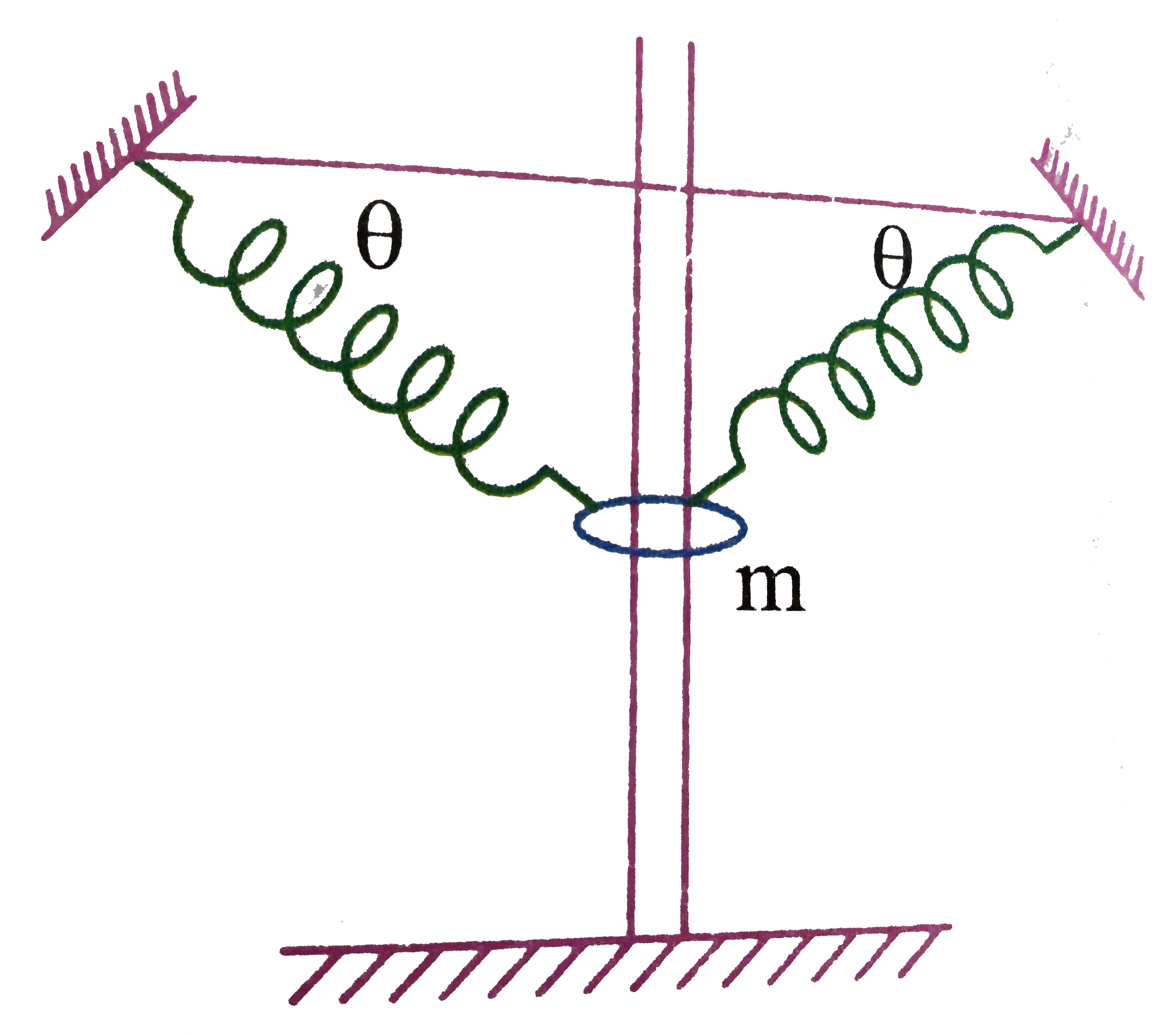
View SolutionA ring of mass m can freely slide on a smooth vertical rod. The ring is symmetrically attached with two springs, as shown, each of stiffness k. Ring is displaced such that each spring makes an angle θ with the horizontal. If the ring is slightly displaced vertically, then time period is.......
View Solution
