The work done by the force =→F=A(x2ˆi+2x2ˆj), where A is a constant and x and y are in meters around the path shown is.
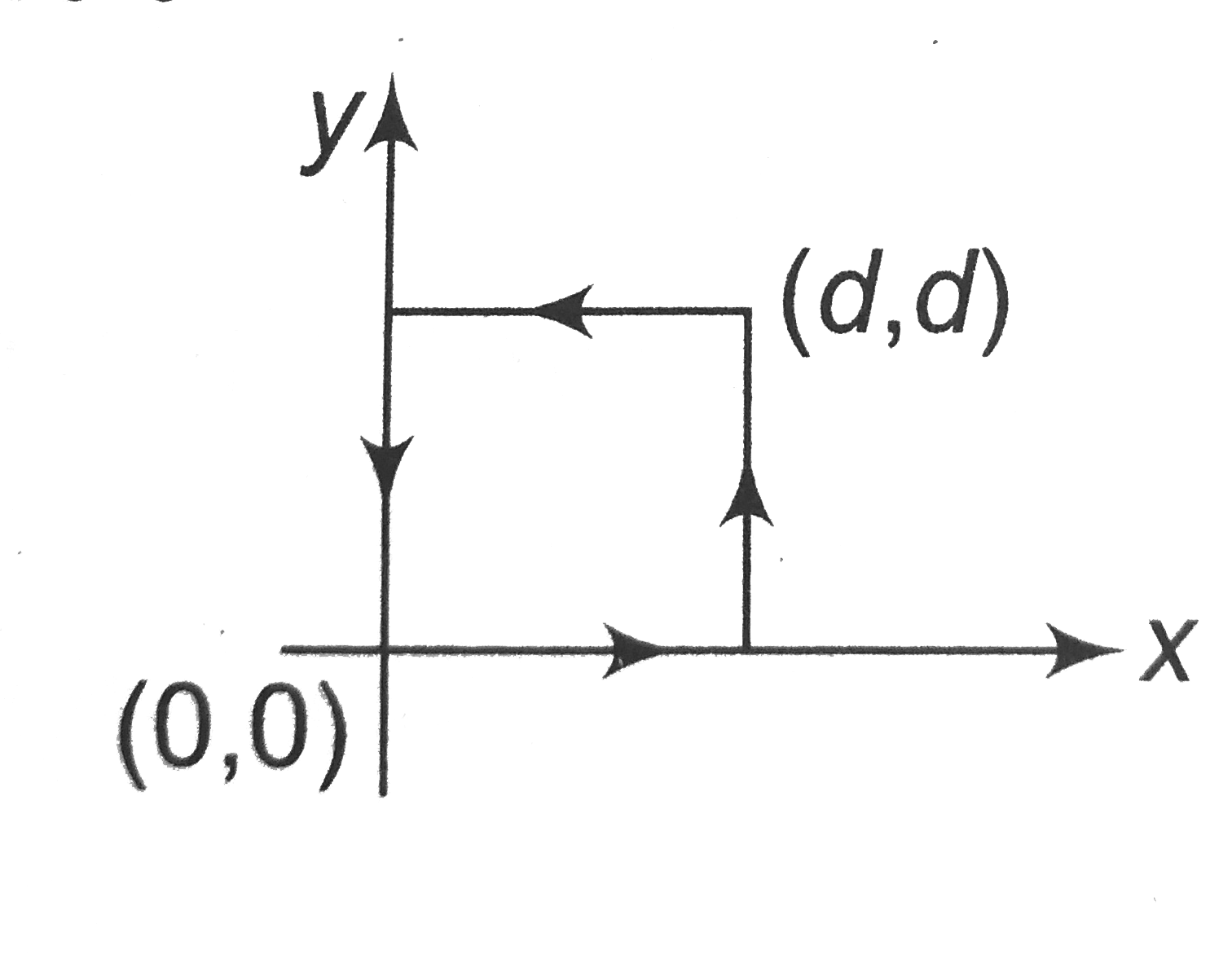
zero
Ad
Ad2
Ad3
The correct Answer is:D
∫→Fd→x=∫A(y2ˆi+2x2ˆj)(dxˆi+dyˆj)
A∫(y2dx+2x2dy)
WOA=0+0,WAB=A[0+2d2d]
WBC=A[d2(−d)+0],WCD=A[0+0]
W=0+2Ad3−Ad3+0=Ad3
Similar Questions
A particle moves in x-y plane from (0,0) to (a,a) and is acted upon by a force →F=k(y2ˆi+x2ˆj)N, where k is a constant and x and y are coordinates in meter. Find work done by this force, if the particle moves along
Two straight lines first from (0,0) to (a,0) and then from (a,0) to (a,a)
View SolutionThe electric field strength depends only on the x and y coordinates according to the law E = a(xˆi+yˆj)x2+y2 , where a is a constant ˆi and ˆj are unit vectors of the x and y axes . Find the potential difference between x = 1 and x = 5 :
View Solution
Knowledge Check
The work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
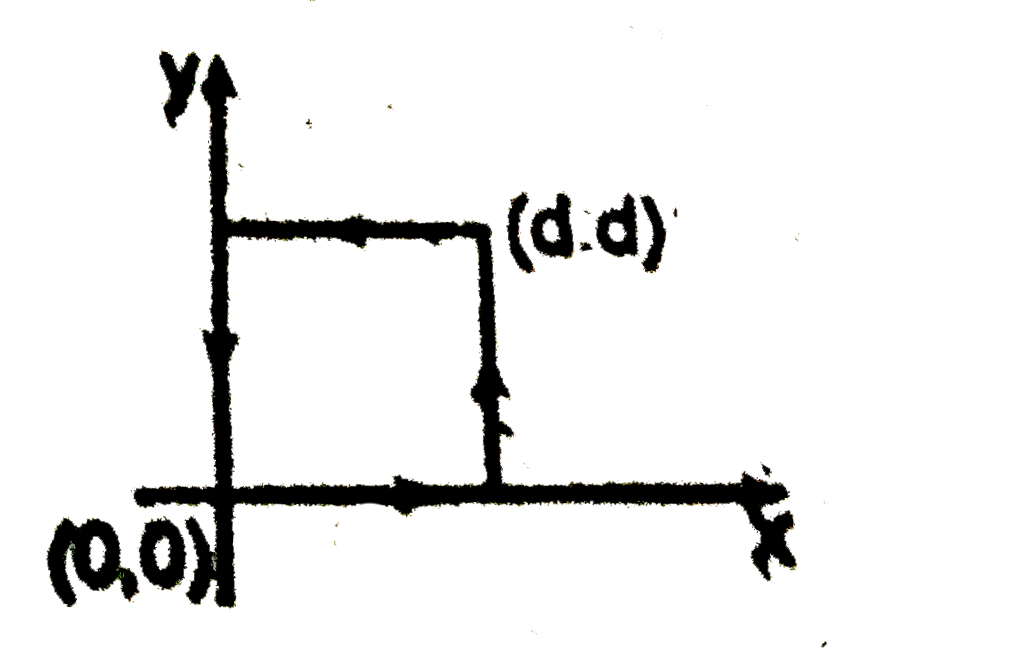 AzeroBAdCAd2DAd3
AzeroBAdCAd2DAd3The work done by the forces →F=2ˆi−ˆj−ˆk in moving an object along the vectors 3ˆi+2ˆj−5ˆk is:
A−9 unitsB15 unitsC9 unitsDNone of theseThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
A−240JB360JC420JDwill depend upon the path
A force F=−k(^ˆi+xˆj) (where k is a positive constant) acts on a particle moving in the x−y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
(a) −2ka2 , (b) 2ka2,(c)-ka^(2),(d)ka^(2)
View SolutionA force →F=(−yˆi+xˆj)N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32πJ in one complete revolution then asSigmaing x,y to be in meters, find the radius of the path.
View SolutionThe work done by an applied variable force F=x+x3 from x = 0 m to x = 2m, where x is displacement, is
View SolutionWhat is the work done when a force →F=2ˆi+3ˆj−5ˆk units acts on a body, producing a displacement →S=2ˆi+4ˆj+3ˆk units ?
View SolutionA force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
View Solution
