For the first row trasition metals the Eɵ value are:
V−1.18Cr−0.91Mn−1.18Fe−0.44Co−0.28Ni−0.25Cu+0.34
Explain the irregularity in the abpve values.
Video Solution
Text Solution
The Eɵ (M2+M) values are not regular which can be explained from the regular variation of ionisation enthalpies (△iH1+△iH2) and also the sublimation enthalpies which are relatively much less for manganese aned vanadium.
|
Topper's Solved these Questions
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRYCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Solved Example
18 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRYCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Ex 6.1 Subjective
12 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRYCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRYCHAPTER - ELECTROCHEMISTRYEXERCISE - Archieves Subjective
35 Videos
Similar Questions
Knowledge Check
 (A) overset(NaNO_(2)//HCl)underset((ii)H_(2)//Ni)underset(0-5^(@))(rarr)(B) , is: A
(A) overset(NaNO_(2)//HCl)underset((ii)H_(2)//Ni)underset(0-5^(@))(rarr)(B) , is: A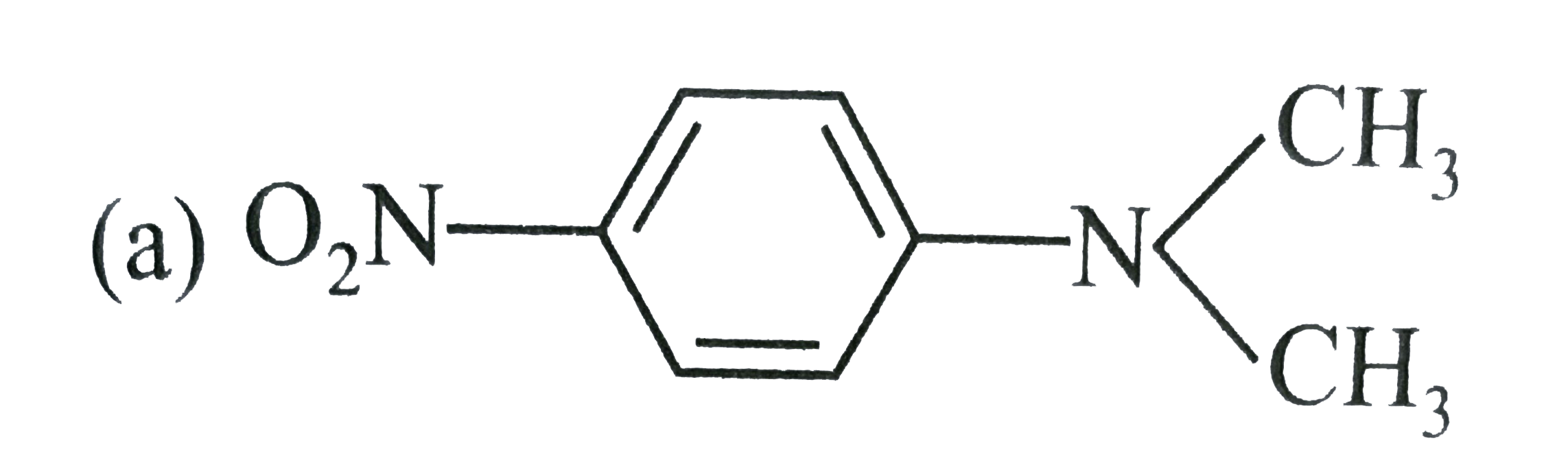 B
B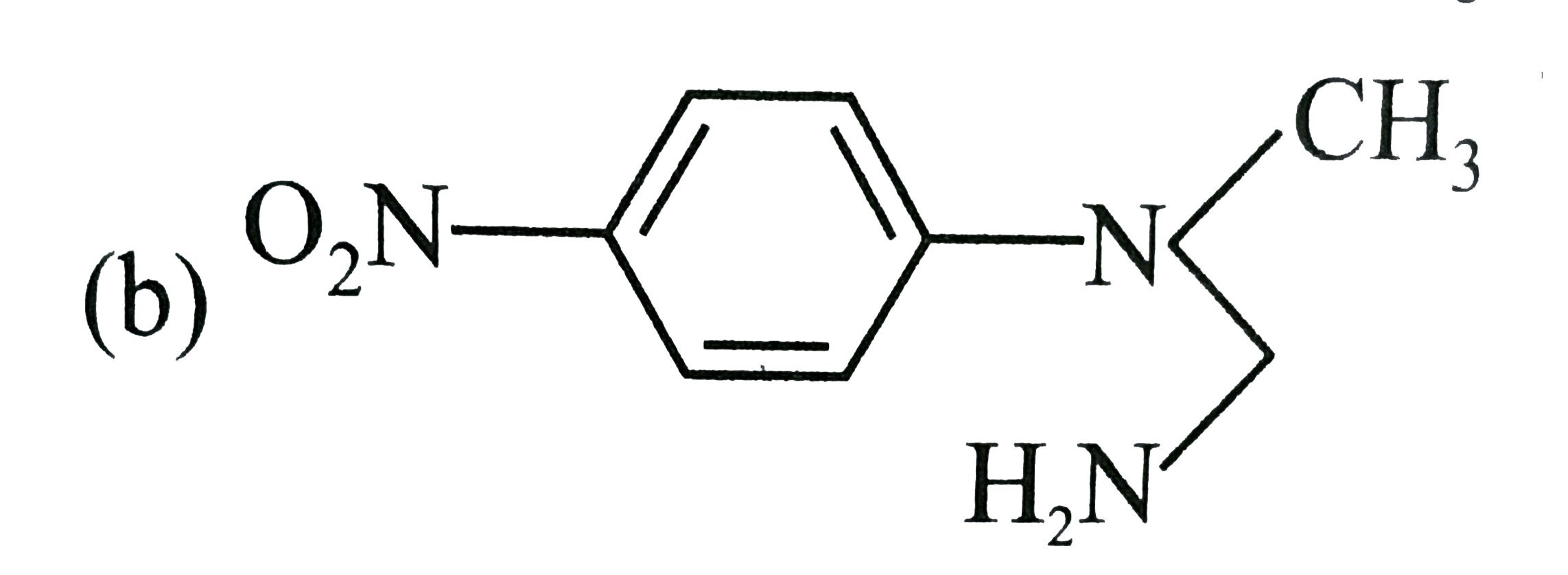 C
C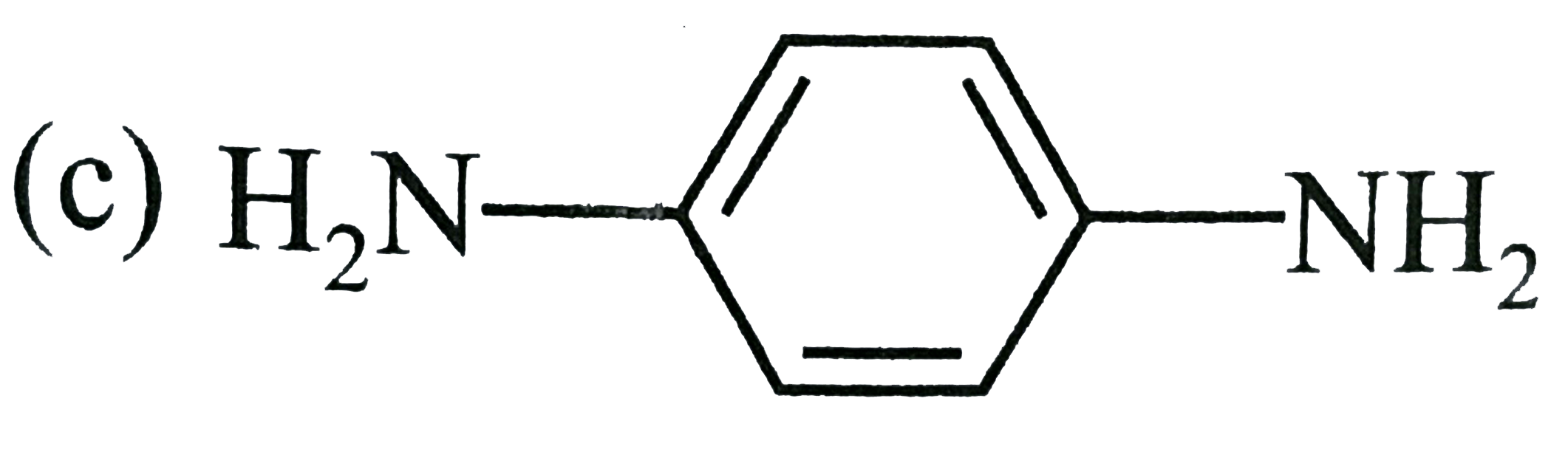 D
D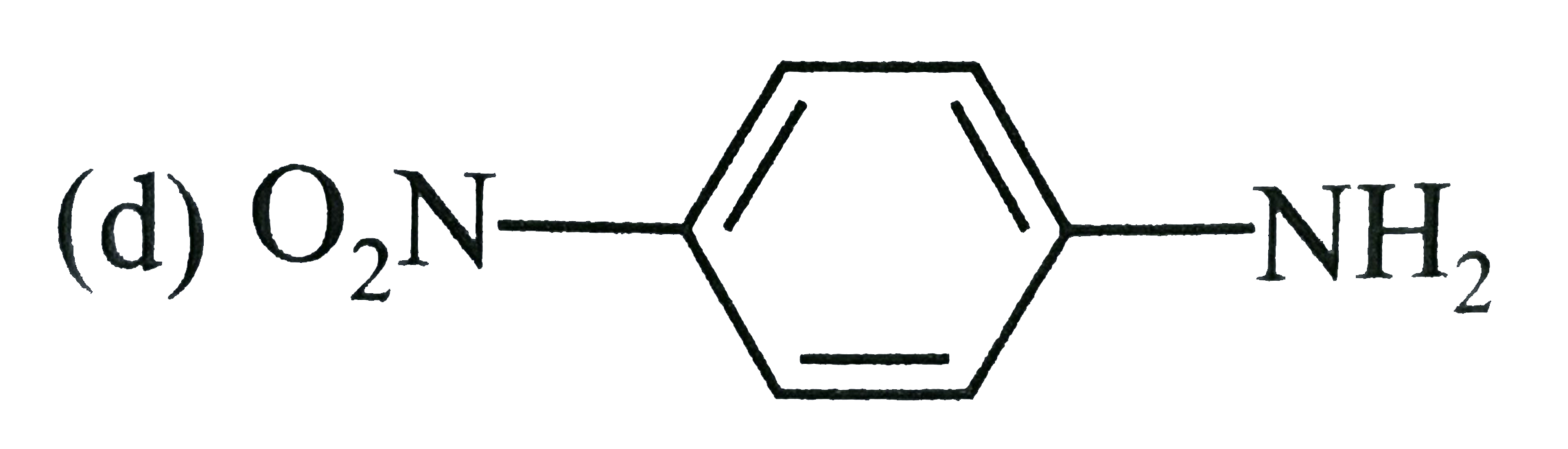
Student I,II,andIII perform an experiment for measuring the acceleration due to gravity (g) usinf a simple pendulum. They use lengths of the pendulum and // or record time for different number of oscillations . The observations are shown in the following table . Least count for length =0.1cm
StudentIIIIIILength of Pendulam(cm)64.064.020.0Number ofn Oscillation(n)844TimePeriod(s)16.016.09.0
Least count for time =0.1s.
If EI,EII , and EIII are the percentage errors in g , i.,e., (Δgg×100) for students I,II , and III, respectively , thenAEI=0BEIisminiμmCEI=EIIDEIIismaxiμmIf a∫0f(2a−x)dx=manda∫0f(x)dx=n, then 2a∫0f(x)dx is equal to
A2m+nBm+2nCm−nDm+n
Evaluate: π/4∫0sinxdx
View SolutionEstimate the value of 1e0x2dx by using 1e0xdx.
View SolutionGiven below are the sets of quantum nummbers for given orbital. Name these orbitals .
(a) n=3l=1m=−1
(b) n=5l=2m=0
(c ) n=4l=1m=±1
(d) n=2l=0m=0
(e). n=4l=2m=±1
View SolutionDehydration product of 1,4 -diol given below will be :
CH3C∣OHHCH2CH2C∣O18HH2H⊕−−→△
View SolutionThe value of ∫πx0sin3xdx is
View Solution
