Find the matrices of transformation T1T2andT2T1 when T1 is rotation through an angle 60∘andT2 is the reflection in the Y-asix Also, verify that T1T2≠T2T1.
Video Solution
Text Solution
T1=[cos60∘,−sin60∘sin60∘,cos60∘]=⎡⎢⎣12−√32√3212⎤⎥⎦=12[1√3−√31]
and T2=[−1001]
∴ T1T2=12[1−√3√31]×[−1001]=12[−1+00−√3−√3+00+1]
=12[1−√3−√31]=⎡⎢⎣−12−√32−√3212⎤⎥⎦
T1T2=[−1001]×12[1−√3√31]=12[−1+0√3+00+√30+1]
=12[−1√3√31]=⎡⎢⎣−12√32√3212⎤⎥⎦
it is clear from Eqs. (i) and (ii) , then
T1T2≠T2T1
|
Similar Questions
Knowledge Check
The figure shows the variation of V with i at temperatures T1 and T2. Then T1−T2 is proportional to
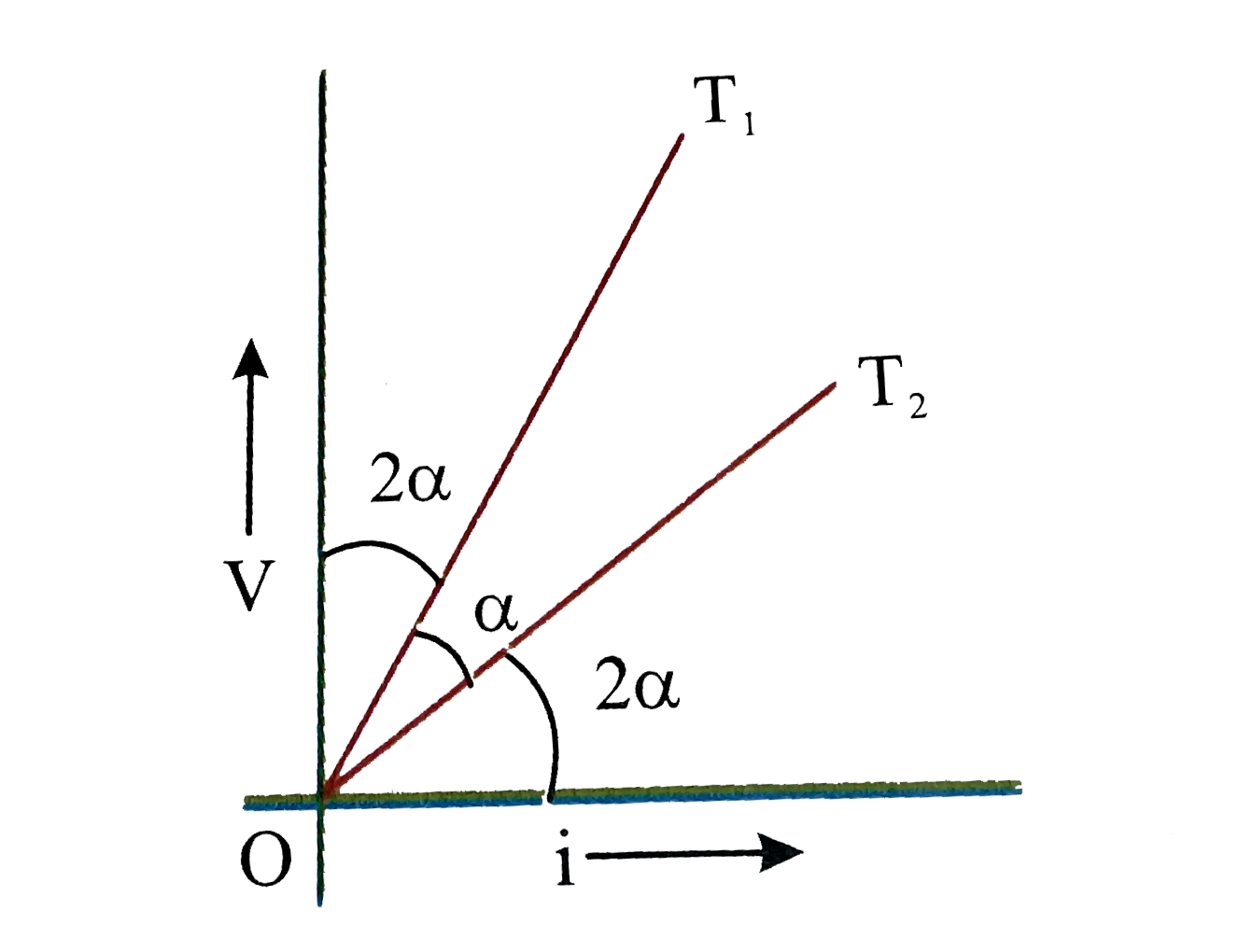 Atan2αBtanαCsinαDcos2α
Atan2αBtanαCsinαDcos2αIf two bodies at different temperatures T1 and T2 are brought in thermal contact, the mean temperature T1+T22. When
Amass of two bodies are equalBpressure on two bodies are equalCtherma capacities of two bodies are equalDvolume of two bodies are equalIf x=1−t21+t2 and y=2t1+t2, then dy/dx is equal to
A−yxByxC−xyDxy
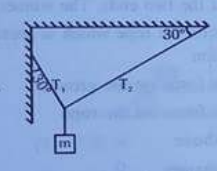
Calculate T1&T2.
View Solution
Calculate a, T1,T2,T1'&T2'.
View SolutionThe normal at t1 and t2 on the parabola y2=4ax intersect on the curve then t1t2
View SolutionFind the first five terms of the sequence for which t1=1,t2=2andtn+2=tn+t+(n+1)
View SolutionFind the locus of the point (t2−t+1,t2+t+1),t∈R.
View Solution