If in a triangle PQR;sinP,sinQ,sinR are in A.P; then

A

the altitudes are in AP

B

the altitudes are in HP

C

the medians are in GP

D

the medians are in AP

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

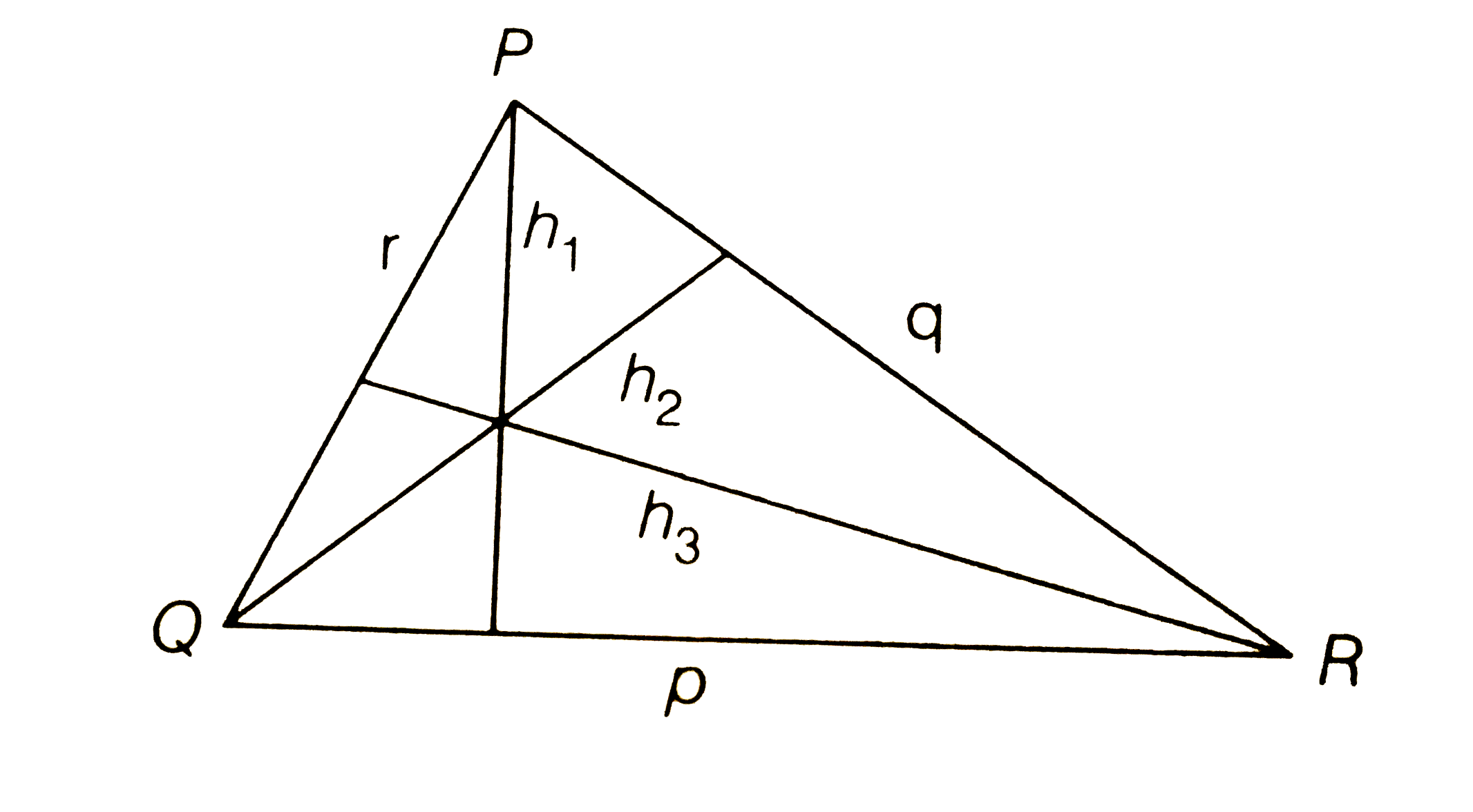
Let triangle be the area of ΔPQR.
∴Δ=12×p×h1 [h1,h2,h3 are altitudes ]
⇒h1=2Δp ….(i)
Similarly, h2=2Δq ….(ii)
and h3=2Δr ....(iii)
According to the question, sinP, sinQ, sin R are in AP.
Then, kp,kq,kr, are in AP [ by sine rule ]
⇒p,q,r are in AP.
⇒2Δh1,2Δh2,2Δh3 are in AP. [ by Eqs. (i),(ii) and (iii) ]
⇒1h1,1h2,1h3 are un AP.
⇒h1,h2,h3 are in HP.
⇒ Altitudes are in HP.
ocr_image.

Updated on:21/07/2023
|
Class 12MATHSSEQUENCES AND SERIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If, in a △PQR, sin P, sin Q, sin R are in the A.P, then its altitudes are in

    Athe altitudes are in A.P.
    Bthe altitudes are in H.P.
    Cthe altitudes are in G.P.
    Dthe altitudes are in A.P.

  • If, in a △PQR, sin P, sin Q, sin R are in the A.P, then its altitudes are in

    Athe altitudes are in AP
    Bthe altitudes are in HP
    Cthe medians are in GP
    Dthe medians are in AP

  • If in a ΔPQR, sin P, sin Q , sin R are in AP, then:

    Athe altitudes are in A.P.
    Bthe altitudes are in H.P.
    Cthe altitudes are in G.P.
    Dnone of these