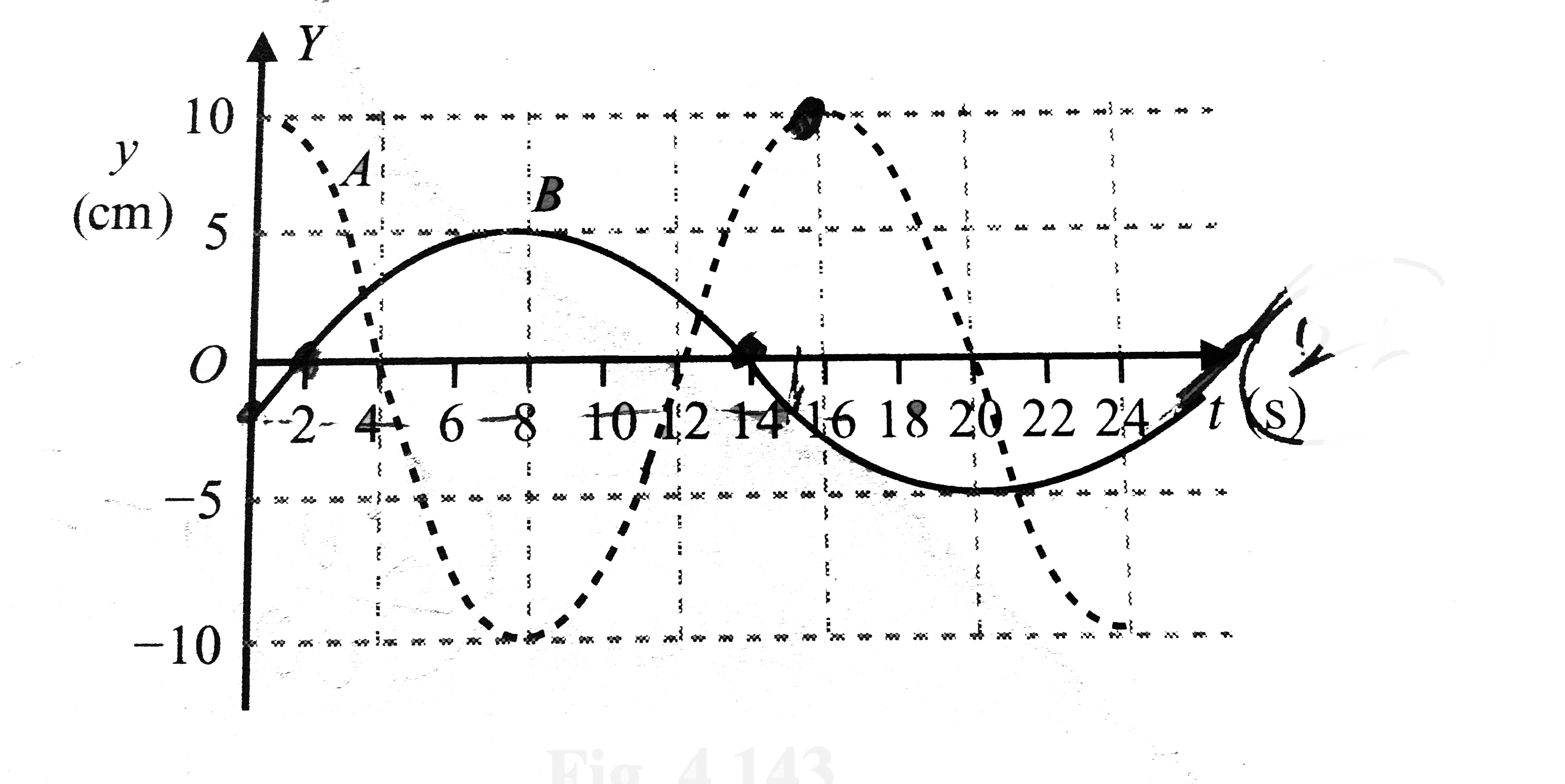
The following figure shows the displacement versus time graph for two

The velocity of a particle executing simple harmonic motion is
A $ω^{2} \sqrt{A^{2} + x^{2}}$
B $ω \sqrt{A^{2} - x^{2}}$
C $ω \sqrt{A^{2} + x^{2}}$
D $ω^{2} \sqrt{A^{2} - x^{2}}$
While a particle executes linear simple harmonic motion
Aits linear velocity and acceleration pass through their maximum and minimum values once in each oscillation.
BIts linear velocity and acceleration pass through their maximum and minimum values twice in each oscillation.
Cits linear velocity and acceleration pass through their maximum and minimum values four times in each oscillation.
Dits linear velocity and acceleration always attain their peak values simlataneaously.
If a particle is executing simple harmonic motion, then acceleration of particle
Ais uniform
Bvaries linearly with time
Cis non uniform
DBoth (2) & (3)

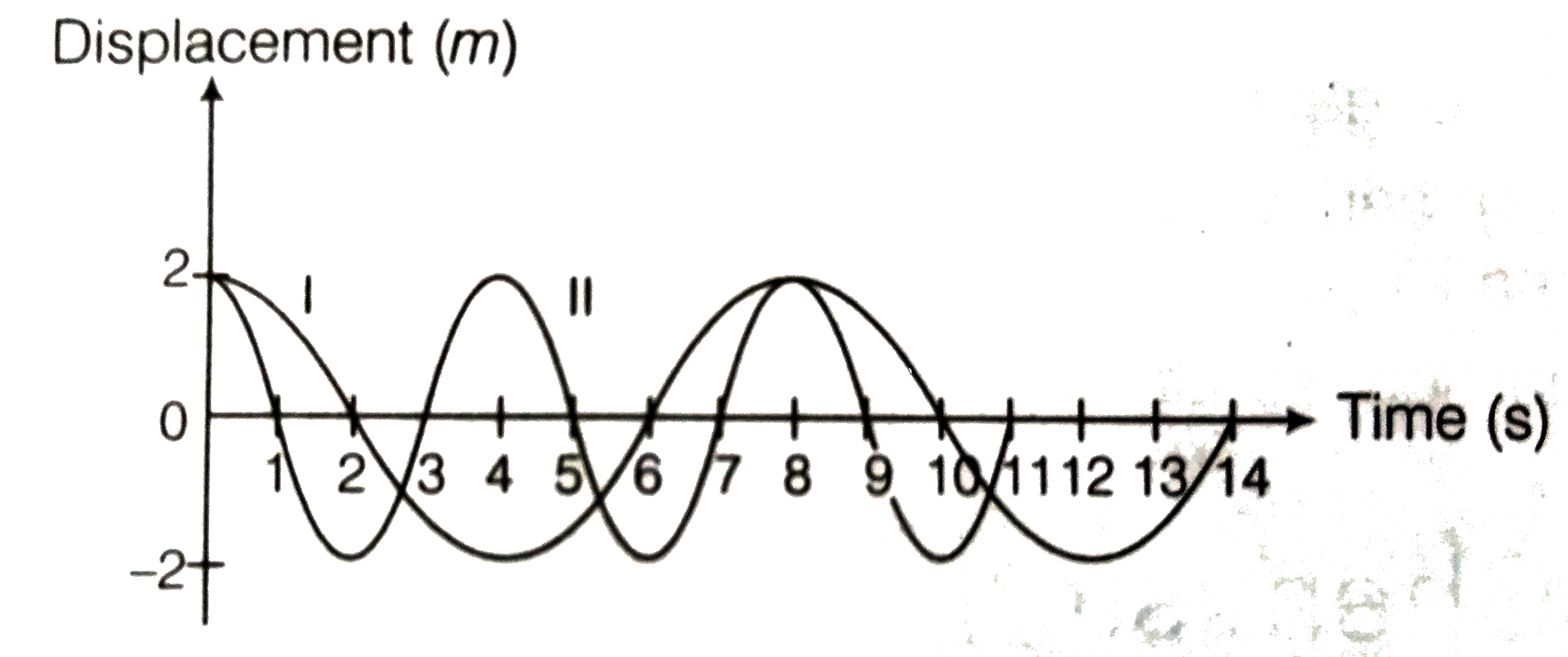
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is