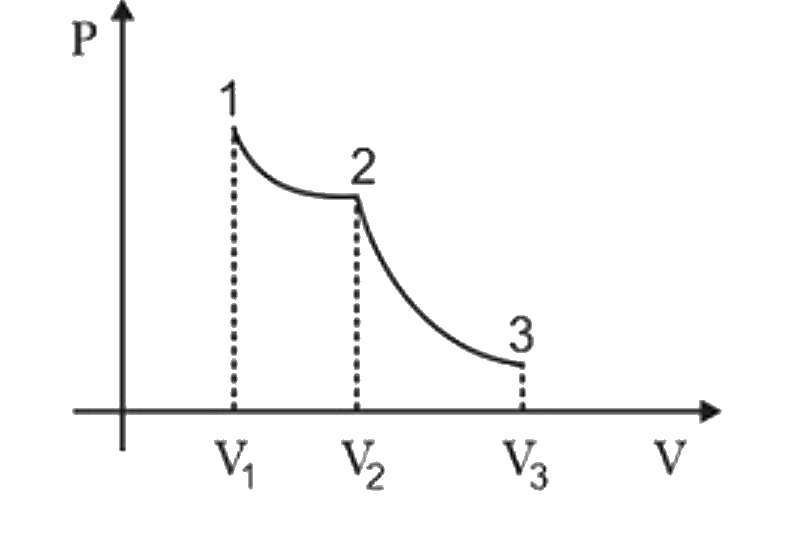
One mole of a perfect gas, initally at a pressure and temperature of $10^{5} N / m^{2}$ and 300 K, respectively, expands isothermally unitl its volume is doubled and then adiabatically until its volume is again doubled. Find final pressure and temperature of the gas Find the total work done during the isothermal and adiabatic processes. Given $γ = 1.4$ . Also draw the P-V diagram for the process.

Video Solution

Text Solution

Verified by Experts

Let $P_{1}, V_{1}, T_{1}$ be the initial pressure, volume and the temperature of the gas, respectively. For isothermal expansion (1 to 2), we have
$V_{2} = 2 V_{1}, P_{1} V_{1} = P_{2} V_{2}$
$P_{2} = P_{1} (V_{1} / V_{2}) = P_{1} / 2 = 0.5 \times 10^{5} N / m^{2}$
For adiabatic expension (2 to 3),
$P_{2} V_{2}^{γ} = P_{3} V_{3}^{γ}$
$\Rightarrow V_{3} = 2 V_{2}$
$\Rightarrow P_{3} = P_{2} {(\frac{V_{2}}{V_{3}})}^{γ} = 0.5 \times 10^{5} \times {(0.5)}^{1.4}$
$\Rightarrow P_{3} = 1.9 \times 10^{4} N / m^{2}$
$T_{2} V_{2}^{γ - 1} = T_{3} V_{3}^{γ - 1}$
$\Rightarrow T_{3} = T_{3} {(\frac{V_{2}}{V_{3}})}^{γ - 1} = 300 {(\frac{1}{4})}^{0.4} = 227.35 K$
Hence, final pressure and temperatures are $1.9 \times 10^{4} N / m^{2}$ and 227.35 K, respectively.
Work done is $W = W_{1 \to 2} + W_{2 \to 3}$ .

Updated on:21/07/2023

Initial pressure and volume of a gas are P and V respectively. First it is expanded isothermally to volume 4 V and then compressed adiabatically to volume V. The final pressure of gas will be (given $γ = \frac{3}{2}$ )
A $1 P$
B $2 P$
C $4 P$
D $8 P$
A monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take $γ = \frac{5}{3}$ )
A64 P
B32 P
C $\frac{P}{64}$
D16 P
A monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take $γ = \frac{5}{3}$ )
A64 P
B32 P
C $P / 64$
D16 P