A whistle emitting a sound of frequency 440hz is tied to a string of 1.5m length and roated with an angular velocity of 20rad/s in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a larger distance from the whistle .(Speed of sound =330m/s) .
400.0 Hz to 484.0 Hz
403.3 Hz to 480.0 Hz
400.0 Hz to 480.0 Hz
403.3 Hz to 484.0 Hz
The correct Answer is:D
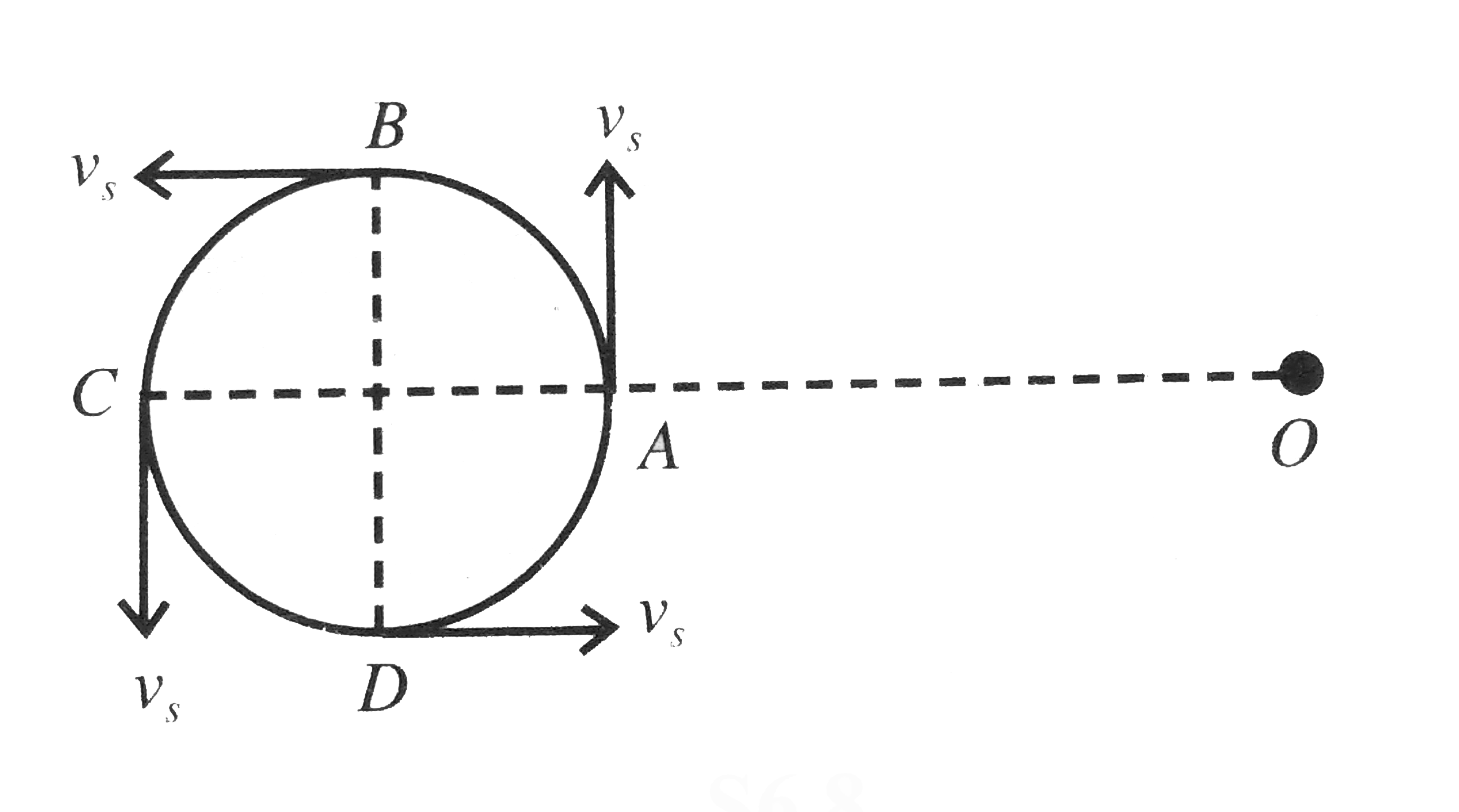
Frequency heard by the observes will be maxmum when the source is in position D. In this case, source will be approaching towards the stationary observer, almost along the line of sight (as observer is stationed at a larger distance.)
nmax=vv−vSn
=330×440330−1.5×20
=484Hz
Similarly, frequency heard by the observer will be minimum when the source reaches at position B. Now, the source will be moving away from the observer.
nmin=vv+vS×n=330330+1.5×20×440
=330×440360=403.3Hz
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct
44 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICSCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A whistle emmitting a sound of frequency 440Hz is tied to a string of 1.5m length and rotated with an angular velocity of 20rad s^(-1) in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a large distance from the whistle.
View SolutionA whistle of frequency 540 Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad/s. What are the lowest and highest frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (Velocity of sound in air is 1100ft/s)
View Solution
Knowledge Check

A whistle emitting a sound of frequency 440Hz is tied to string of 1.5m length and rotated with an angular velocity of 20rad/sec in the horizontal plane. Then the range of frequencies heard by an observer stationed at a large distance from the whistle will (v=330m/s)A400.0Hz to 484.0HzB403.3Hz to 480.0HzC400.0Hz to 480.0HzD403.3 Hz to 484.0HzA whistle emitting a loud sound of frequency 540 Hz is whirled in a horizontal circle of radius 2 m and at a constant angular speed of 15rad/s. The speed of sound is 330m/s. The ratio of the highest to the lowest frequency heard by a listener standing at rest at a large distance from the center of the circle is
A1.0B1.1C1.2D1.4A train standing at the outer signal of a railway station blows a whistle of frequency 400 Hz in still air. The train begins to move with a speed of 30 ms−1 towards the platform. The frequency of the sound heard by an observer standing on the platform is
(Speed of sound in air = 330 m s−1)A420 HzB430 HzC440 HzD450 Hz
A whistle of frequency 540Hz is moving in a circle of radius 2 ft at a constant angular speed of 15 rad//s. What are the lowest and height frequencies heard by a listener standing at rest, a long distance away from the centre of the circle? (velocity of sound in air is 1100ft/sec.)
View SolutionA whitle of frequency 540 Hz rotates in a horizontal circle of radius 2 m at an angular speed of 15rads. What is the lowest and the highest frequency heard by a listener a long distance away at rest with respect to the centre of the circle? (Velocity of sound in air is c=330ms.)
View SolutionA whistle of frequency 540HZ rotates in a circle of radius 2mat a linear speed of 30m/s . What is the lowest and highest frequency heard by an observer a long distance away at rest with respect to the centre of circle ? Take speed of sound of sound in air as 330m/s. Can the apparent frequency be ever equal to actual ?
View SolutionA whistle emitting a sound of frequency 450 Hz approaches a stationary observer at a speed of 33 m/s. Velocity of sound is 330 m/s. The frequency heard by the observer, in Hz, is :
View SolutionA whistle of frequency 500 Hz tied to the end of a string of length 1.2 m revolves at 400 rev / min . A listener standing some distance away in the plane of rotation of whistle hears frequencies in the range (speed of sound = 340 m / s )
View Solution
