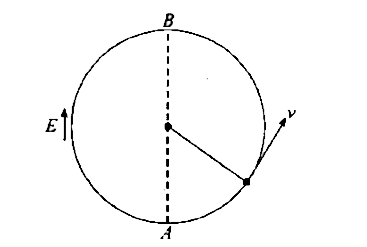
In the previous problem, if time period, $T = 2 (π) \frac{m}{B Q}$ where Q is the charge of the particle and m is its mass, the ratio of time spent by the particle in field when $(θ)$ is positive to when $(θ)$ is negative is given by

A

$(\frac{π / 2 + θ}{π / 2 - θ})$

B

$(\frac{π + θ}{π - θ})$

C

$(\frac{π - θ}{π + θ})$

D

$(\frac{π / 2 - θ}{π / 2 + θ})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

When $θ is + v e, angle at centre = π + 2 θ$
When $θ is + v e, angle at centre = π - 2 θ$
When $θ = 0$ incidence is normal a semicircle is complete
and $T = 2 π \frac{m}{B Q} (time period)$
when $θ$ is positive time spent in magnetic field
$\frac{T}{2 π} \times (π + 2 θ)$
When $θ$ is negative time spent in magnetic field
$= \frac{T}{2 π} \times (π - 2 θ)$
Hence, ratio $= \frac{π + 2 θ}{π - 2 θ} = \frac{π / 2 + θ}{π / 2 - θ}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the previous problem, the maximum range of movement of the centre of the part of the circle from line AD in which charged particle of charge Q moves with a velocity v when $(θ)$ is positive to when $(θ)$ is negative is given by
A $\pm \frac{m v}{2 Q B}$
B $\pm \frac{m v}{Q B}$
C $\pm \frac{2 m v}{Q B}$
D $\pm \frac{2 m v}{3 Q B}$
Question 2 - Select One
In the previous question,if the particle has $- Q$ charge the time spend by the particle in the field will be .

A $T θ$
B $2 T θ$
C $T (\frac{π + 2 θ}{2 π})$
D $T (\frac{π - 2 θ}{2 π})$
Question 3 - Select One
If the ratio of time periods of circular motion of two charged particles in magnetic field in $1 / 2$ , then the ratio of their kinetic energies must be :
A $1 : \sqrt{2}$
B $\sqrt{2} : 1$
C $2 : 1$
Dit can have any value

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Integer

Home
Ask Doubt
Profile