A battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
proportional to 2(180∘−θ)
inversely proportional to r
zero, only if θ=180∘
zero for all values θ
The correct Answer is:D
(d) Magnetic field at the centre due to current in arc ACB is
B1=μ04π2πI1rθ2π (directed upwards)
magnetic field at the centre due to current in arc ADB is
B2=μ04π2πI2r2π−θ2π (directed downwards)
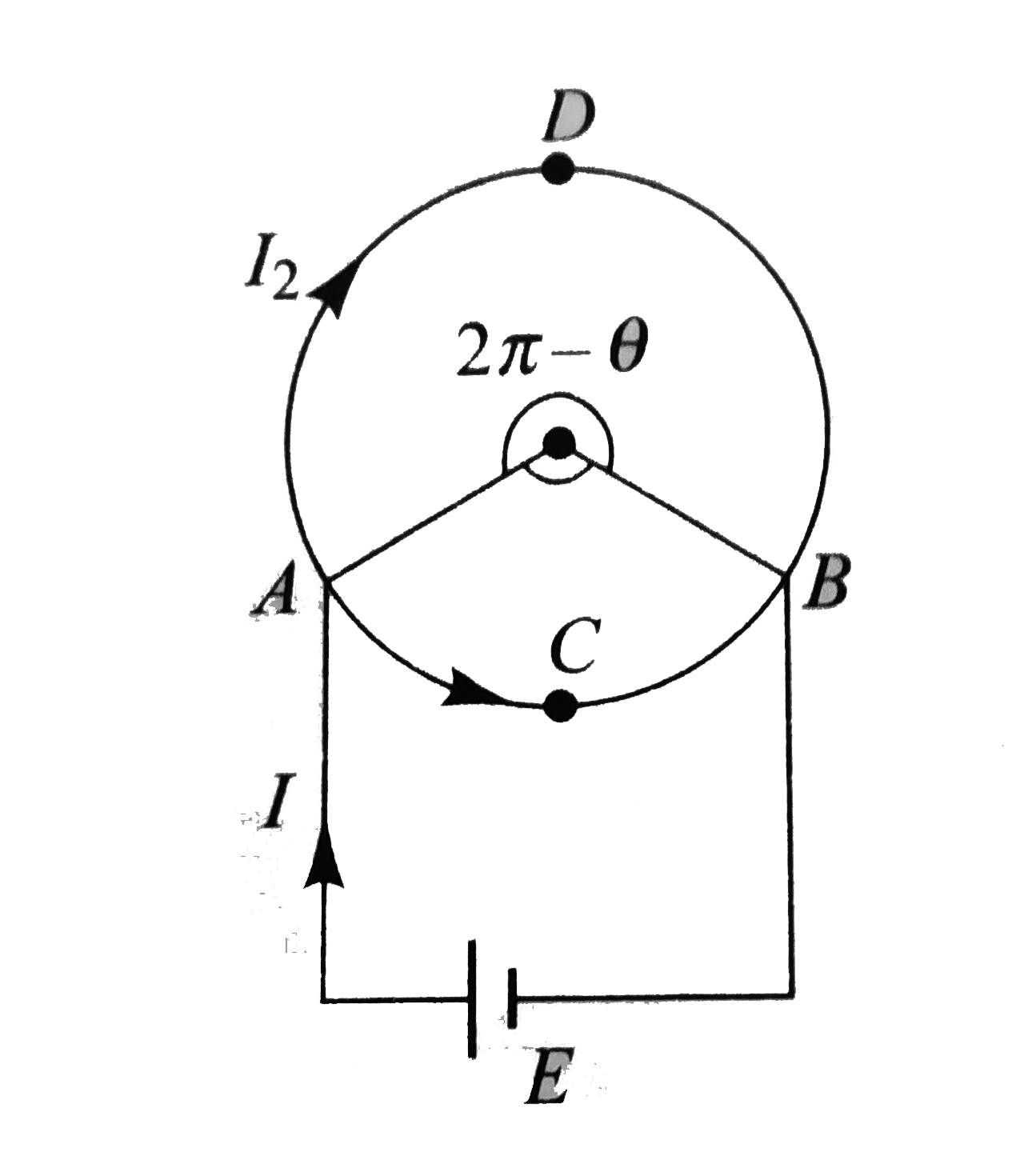
Therefore, net magnetic field at the centre
B=μ04π2πI1rθ2π−μ04π2πI2r2π−θ2π
Also, I1=ER1=Eρl1/A=EAρrθ
And I2=ER2=Eρl2/A=EAρr(2π−θ)
∴B=μ04π[EAρrθ×θr−EAρr(2π−θ)×(2π−θ)r]=0
(d) is the correct option.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (multiple Correct )
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (linked Comprehension)
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
A battary is connected between two points A and B on the circumference of a uniform conducting ring of radius r and resistance R as shown in Fig. One of the arcs AB of the ring subtends angle θ at the centre. Show that that the magnetic field at the centre of the coil is zero and independent θ.
View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View Solution
Knowledge Check
In the figure shown, the magnetic induction at the centre of the arc due to the current in portion AB will be
 Aμ0irBμ0i2rCμ0i4rDzero
Aμ0irBμ0i2rCμ0i4rDzeroAn arc of a circle of radius R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
Aμ0i2RBμ0i8RCμ0i4RD2μ0i5RFor a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
A circular arc of wire of radius of curvature r subtends an angle of p/4 radian at its centre. If i current is flowing in it then the magnetic induction at its centre is -
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
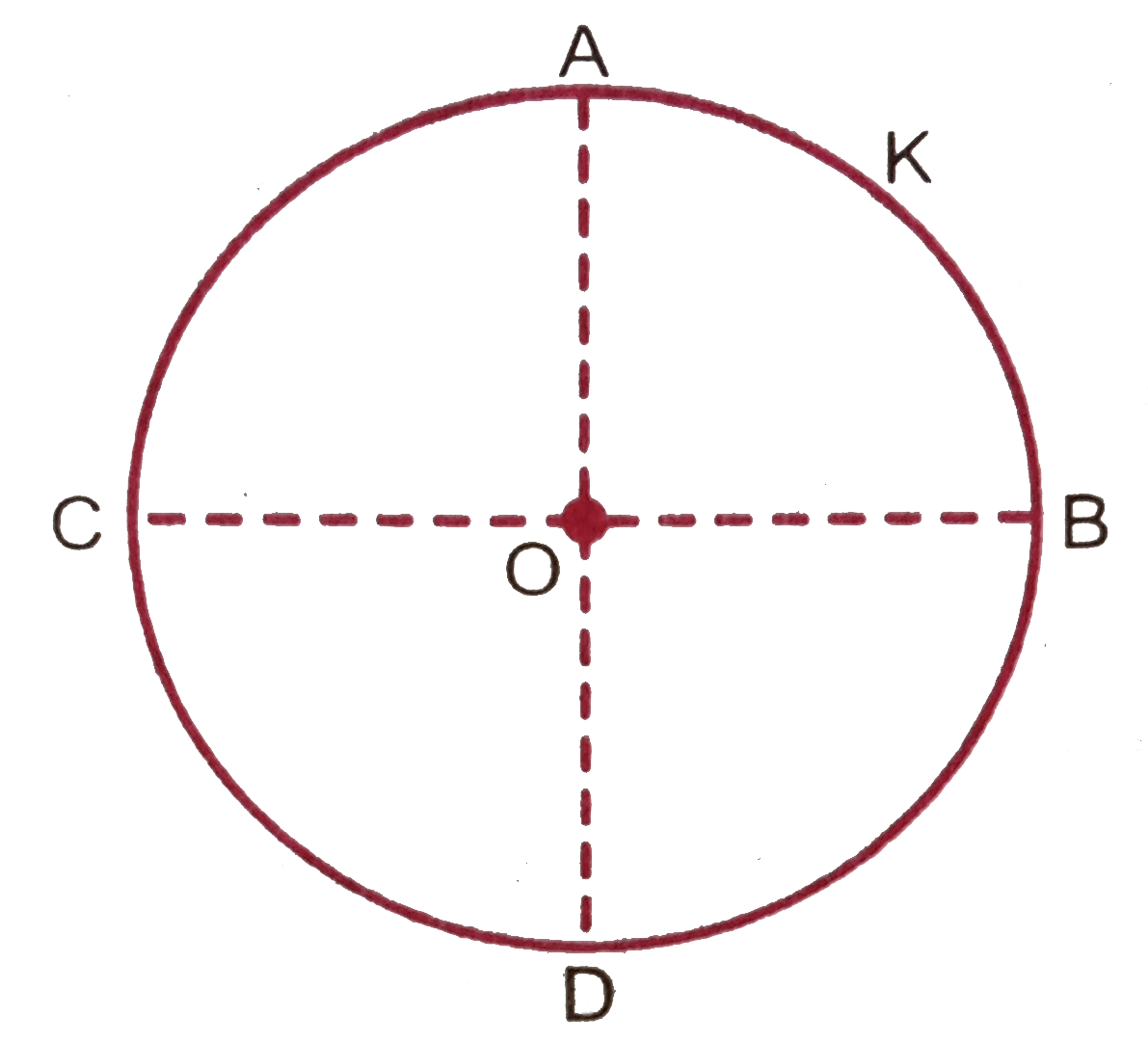
View SolutionA thin conducting ring orf radius R is given a chareg +Q, Fig. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on part ACDB of the ring is
View SolutionA current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

View Solution
