In an interference arrangement similar to double-slit experiment, S1 and S2 are illuminated with coherent source microwave source each of frequency 1 MHz. the sources are synchronized to have zero phase difference . This slits are separated by distance d=150.0m The intensity I(θ) is measured as a funciton of θ, where θ is defined as shown in figure. If I0 is maximum intensity, calculate I(θ)
For :
a. θ=0 b. θ=30∘
c. θ=90∘
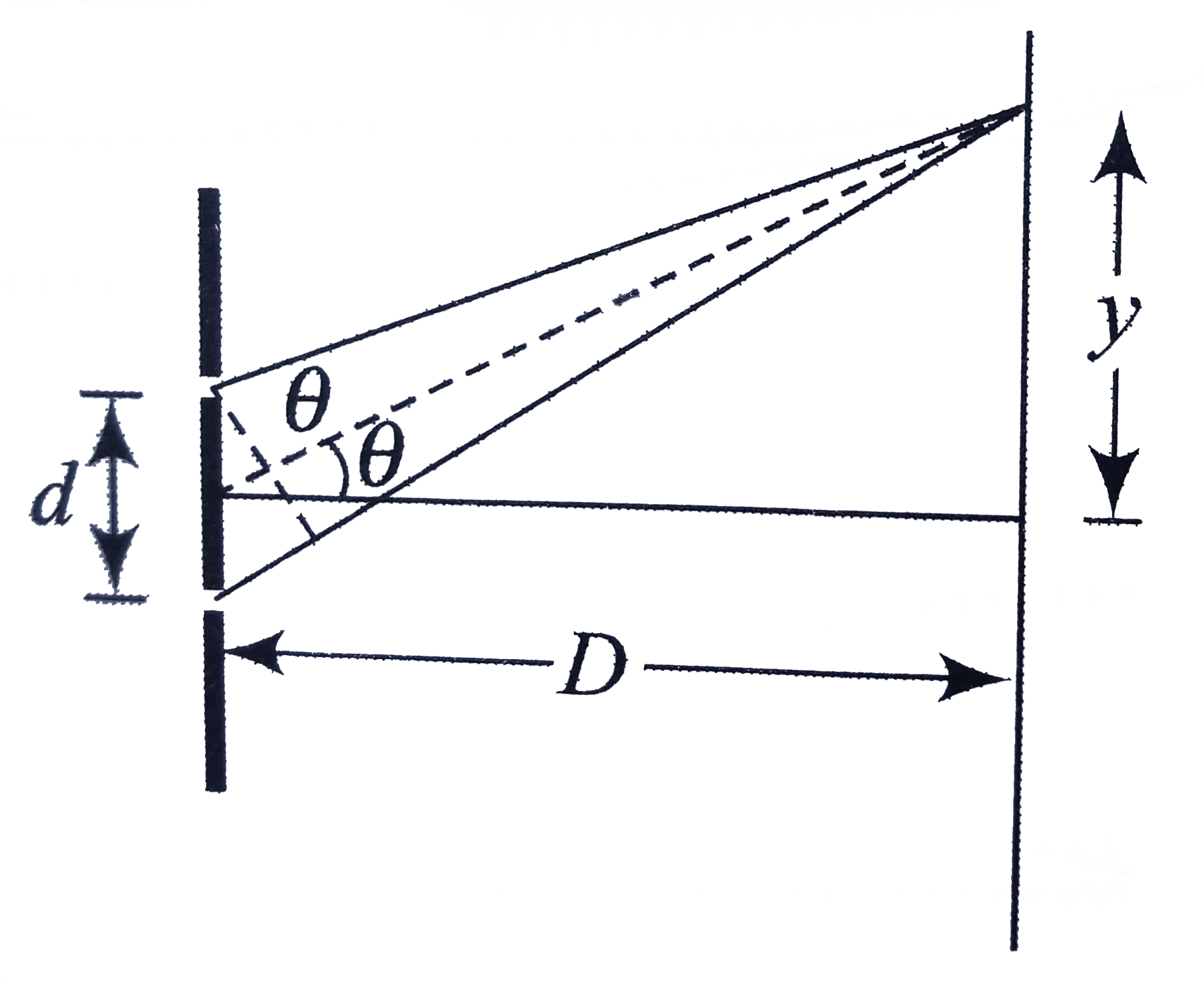
In an interference arrangement similar to double-slit experiment, S1 and S2 are illuminated with coherent source microwave source each of frequeny 1 MHz
λ=cf=3×108106=300m
Δx=dsinθ,ϕ=2πλdsinθ=πsinθ
IR=4Icos2ϕ/2=4Icos2(πsinϕt2)
For Iθ to be maximum, I0=4I⇒I=I04⇒I0=4I
IR=I0cos2(πsinθ2)
a. θ=0∘⇒IRI0
b. θ=30∘⇒IR=I02
c. θ=90∘⇒IR=0
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Single Correct
128 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Consider an interference arrangement similar to YDSE. Slits S1 and S2 are illuminated with coherent microwave sources each of frequency 2 MHz. The sources are synchronised to have zero phase difference. The slits are separated by distance d= 75m. The intensity I(θ) is measured as a function of θ where θ is defined as shown in figure. if I0 is maximum intensity then calculated I(θ) for (i)θ=0∘,(ii)θ=π/6and(iii)θ=π/2
View SolutionIn an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View Solution
Knowledge Check
In an interference arrangement similar to Young's double-slit experiment, the slits S_1 and S_2 are illuminated with coherent microwave sources, each of frequency 10^6 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0 m. The intensity I (theta) is measured as a function of theta, where theta is defined as shown. If I_0 is the maximum intensity, then I (theta) for 0lethetale90degree is given by
 AI(θ)=i02forθ=30degreeBi(θ)=I04forθ=90degreeCI(θ)=I0forθ=0degreeDI(θ) is constant for all
AI(θ)=i02forθ=30degreeBi(θ)=I04forθ=90degreeCI(θ)=I0forθ=0degreeDI(θ) is constant for all_E01_052_Q01.png)
In an interference arrangement similar to young's double slit experiment the slits S1 and S2 are illuminated with coherent microwave sources each of frequency 106Hz the sources are synchronized to have zero phase difference. the slits are separated by a distance d=150.0m. The intensity I(θ) is measured as a funtion of θ, where θ is defined as shown. if I0 is the maximum intensity then I(θ) for 0≤θ≤90∘ is given by:AI(θ)=I0/2 for θ=30∘BI(θ)=I0/4 for θ=90∘CI(θ)=I0 for θ=0∘DI(θ) is constant for all values of θIn a interference arrangement similar to Young's double-slit experiment ,the slits S1 and S2 are illuminated with coheremt microwave source ,each of frequencies 106 Hz.The source are syhronized to have zero phase difference.The slits are separated by a distance from S1 and S2 where theta is defined as shown if I0 is the maximum intensity then
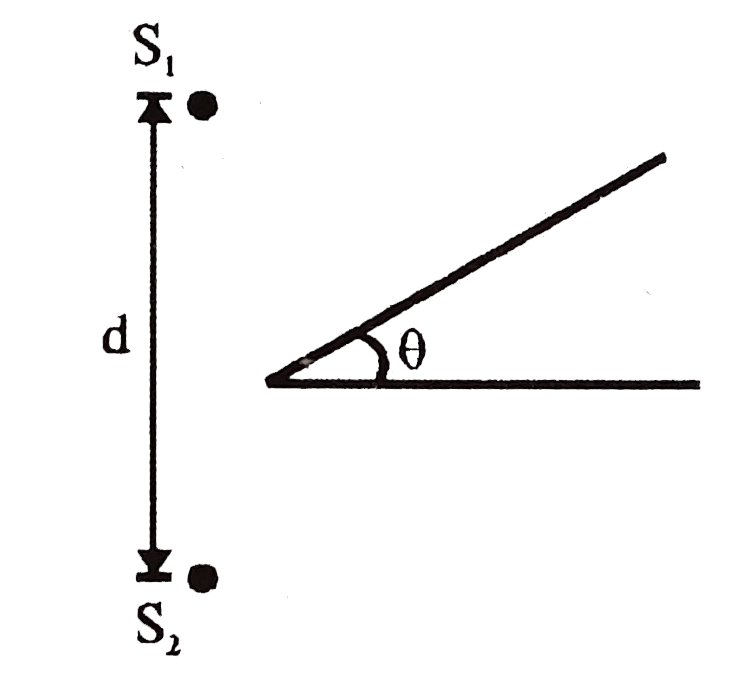 AI(θ)=I02 for θ=30∘BI(θ)=I04 for θ=90∘CI(θ)=(I0) for θ=90∘DI(θ) is constant for all value of θ
AI(θ)=I02 for θ=30∘BI(θ)=I04 for θ=90∘CI(θ)=(I0) for θ=90∘DI(θ) is constant for all value of θ
S1 and S2 are two coherent sources of frequency f each.(θ1=θ2=0∘)Vsound=330m/s.
(i) so that constructive interfence at 'p'
(ii) so that destructive interfrece at 'p'
View SolutionIn Young's double slit experiment, if the two slits are illuminated with separate sources, no interference pattern is observed because
View Solution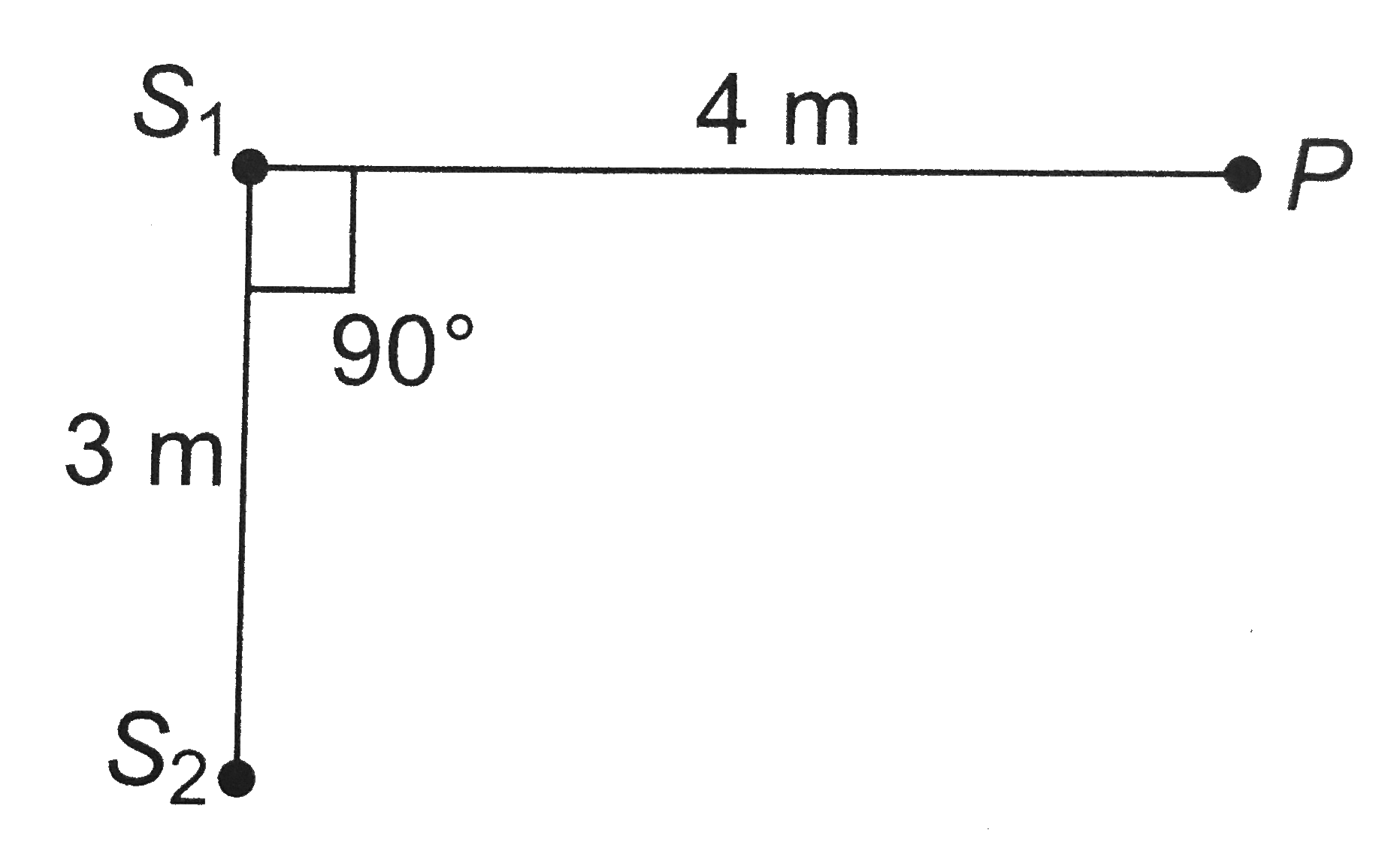
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View SolutionIn young's double slit experiment if the seperation between coherent sources is halved and the distance of the screen from coherent sources is doubled, then the fringe width becomes:
View SolutionS1andS2 are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is 4Wm−2, the intensity of each source is
View Solution
