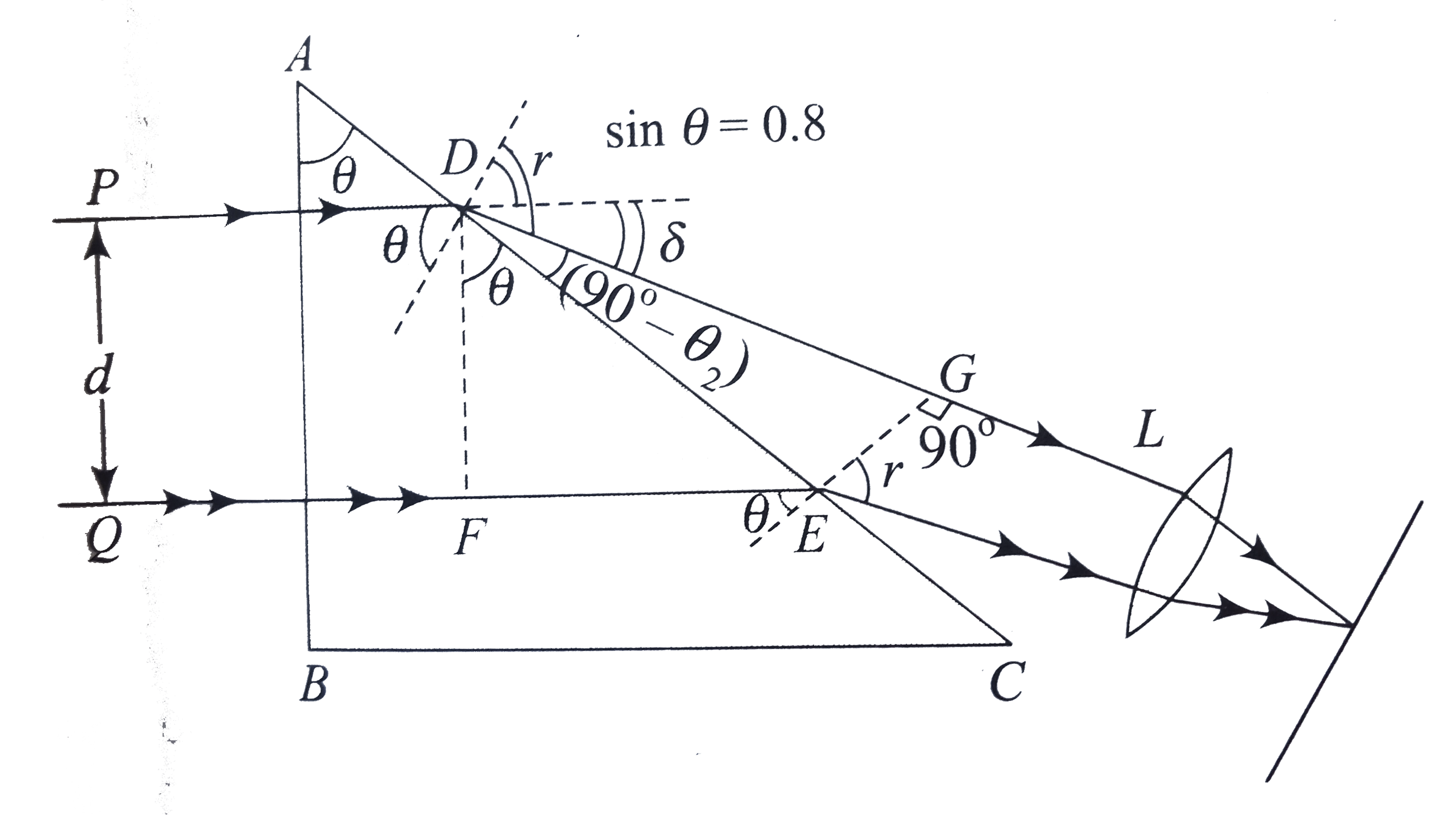
Two parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I abd I, respectively, find the resultant intensity at the focus.
In case of interference,
I=I1+I2(√I1I2)cosϕ
Here, I1=IandI2=4I. So,
IR=5I+4Icosϕ
=I[1+8cos2(ϕ2)]
with ϕ=2πλ(Δx)
where Δx=[DG−EF(in medium)]
Now, from Fig. 2.23,
FE(in medium)=μ(FE)=μdtanθ, [as FE=dtanθ] (iv)
DG=DEcos(90∘−r)=DEsinr
or DG=(dsinrcosθ)[asDE=d/cosθ]
or DG=μtanθ[as atD,μsinθ=1sinr] (v)
Substituting the value of FE and DG from Eqs. (iv) and (v) in Eq. (iii), we get
Δx=μdtanθ−μdtanθ=0
So, Eq. (ii) gives ϕ=0∘ Hence, from Eq. (i),
IR=I[1+8cos20∘]=9I.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Solved Examples
10 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
_E01_106_Q01.png)
Two parallel beams of light P and Q (separation d) containing radiations of wavelengts 4000Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure the refractive index of the prism as a function of wavelength is given by the relation μ(λ)=1.20+bλ2 where λ is in Å and b is a positive constant. The value of b is such that the condition for total reflection at the face AC is just satisfied for one wavelength and is not satisfied for the other. A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face AC, are 4I and I respectively, find the resultant intensity at the focus.
View SolutionTwo parallel beams of light P and Q (separation d) containing radiation of wavelengths 4000A and 5000A (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig. The refractive index of the prism as a function of wavelength is given by the relation. μ(λ)=1.20+bλ2 Where λ is in A and b is positive constant. The value of b is such that the condition wave length and is not satisfied for the other.
(a) Find the value of b.
(b) find the deviation of the beams transmitted through the face AC. (c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.
View Solution
Knowledge Check
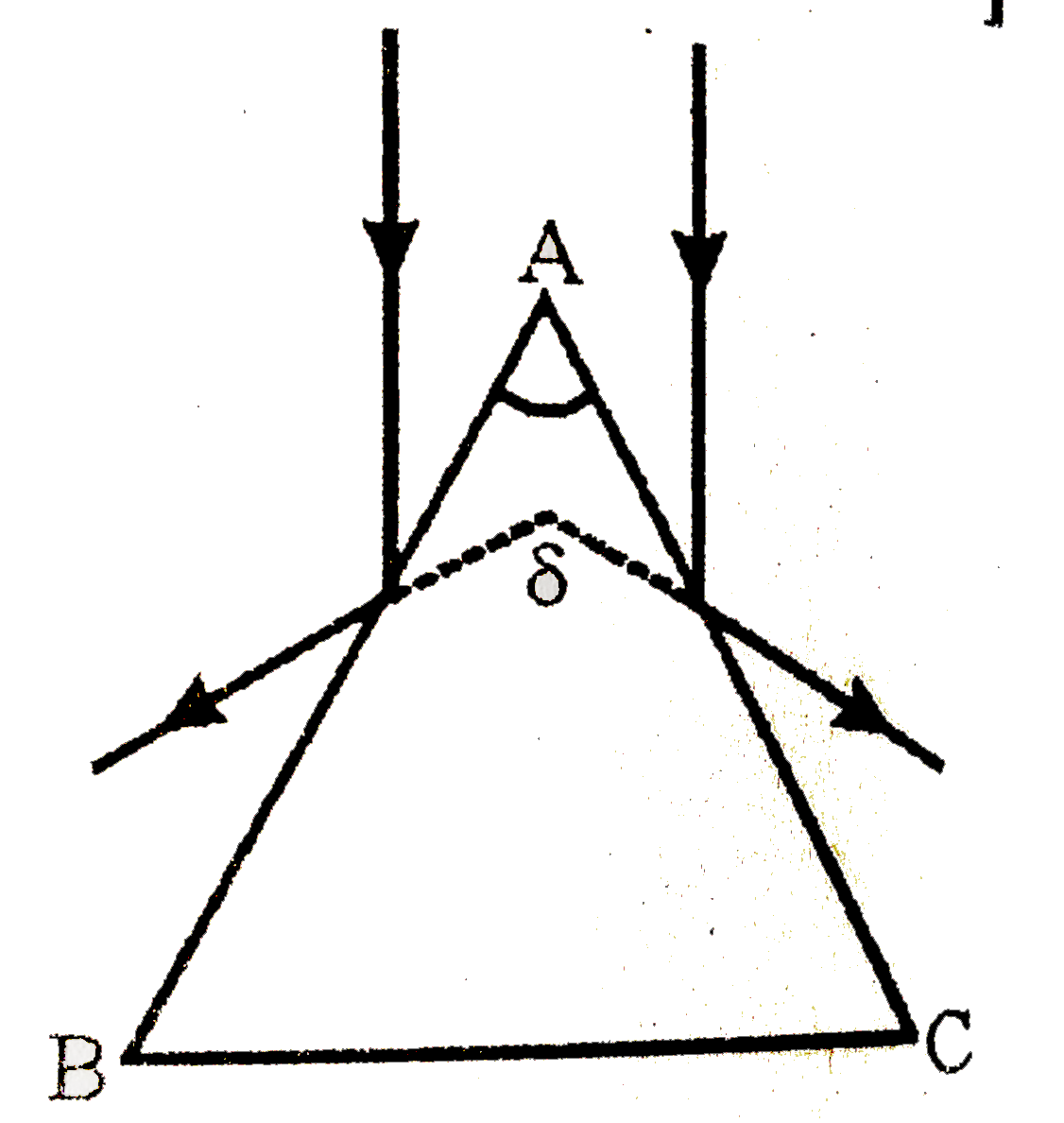
A parallel beam of light is incident on a prism as shown in figure. Such that the rays get reflected from opposite faces. The angle of deviation δ between reflected rays from faces AB and AC is-AAB2ACA2DNon relation between A and δIn the front of the upper slit of YDSE apparatus, a thin film of a liquid of refractive index 1.40 is placed. It is a hot day and the liquid starts evaporating from the surface. A beam of light at wavelength 560 nm is incident onto the YDSE apparatus and the intensity I at the centre of the screen is monitored. Figure gives intensity I as a function of time t. The intensity changes because of evaporation from the two sides of the film. Assume that the film is flat and has parallel sides. Also assume that the film's thickness decreases at a constant rate
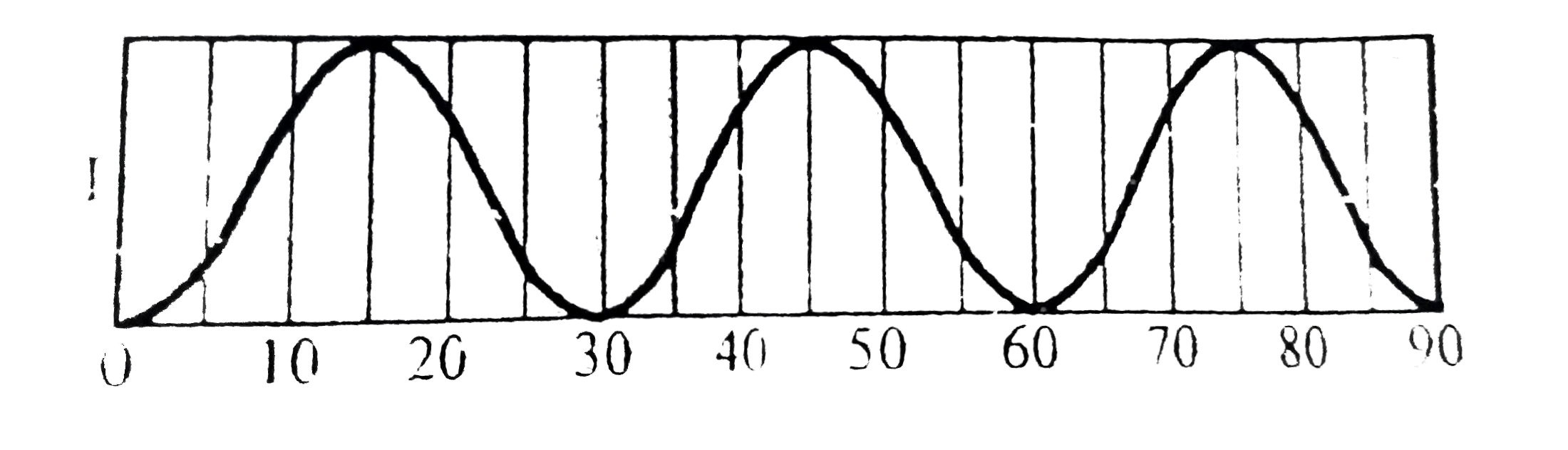
If the maximum intensity is I0 thenAIntensity at t=0secisI0√2BIntensity at t=10secis3I04CIntensity at t=5secisI04DIntensity at t=5sec,I02√2In the given figure a parallel beam of ligth is incident on the upper part of a prism of angle 1.8∘ and R.I.3/2 . The light coming out of the prism falls on a concave mirror of radius of curvature 20cm. The distance of the point (where the rays are focused after reflrction from the mirror) from the pricipal axis is: [use π=3.14]
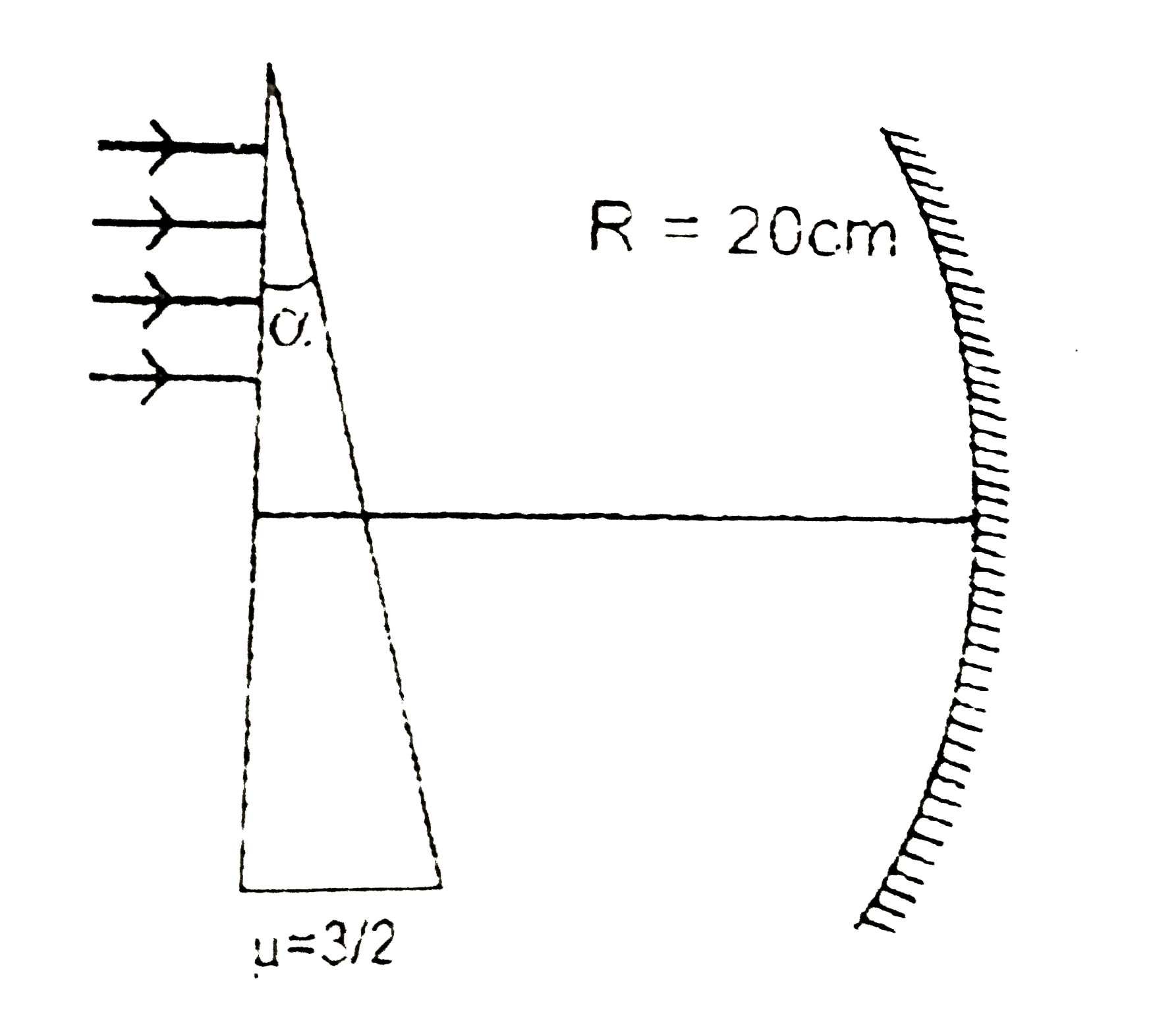A9cmB1.57mmC3.14mmDnone of these
A mixture of plane polarised and unpolarised light falls normally on a polarising sheet. On rotating the polarising sheet about the direction of the incident beam, the transmitted intensity varies by a factor 4. Find the ratio of the intensities IP and I0 respectively of the polarized and unpolarised components in the incident beam. Next the axis of polarising sheet is fixed at an angle of 45∘ with the direction when the transmitted intensity is maximum. Then obtain the total intensity of the transmitted beam in terms of I0.
[32,5I04]
View Solution_E01_102_Q01.png)
In a YDSE a parallel beam of light of wavelength 6000Å is incident on slits at angle of incidence 30∘. A and B are two thin transparent films each of refractive index 1.5. thickness of A is 20.4μm. Light coming through A and B have intensities I and 4I resepctively on the screen. Intensity at point O which is symmetric relative to the slits is 3I. The central maxima is above O.
(i). what is the maximum thickness of B to do so. Assuming thickness of B to be that found in part (i) answer the following parts.
(ii). Find fringe width, maximum intensity and minimum intensity on screen.
(iii). Dinstance of nearest minima from O
(iv) intensity at 5 cm on either side of O.
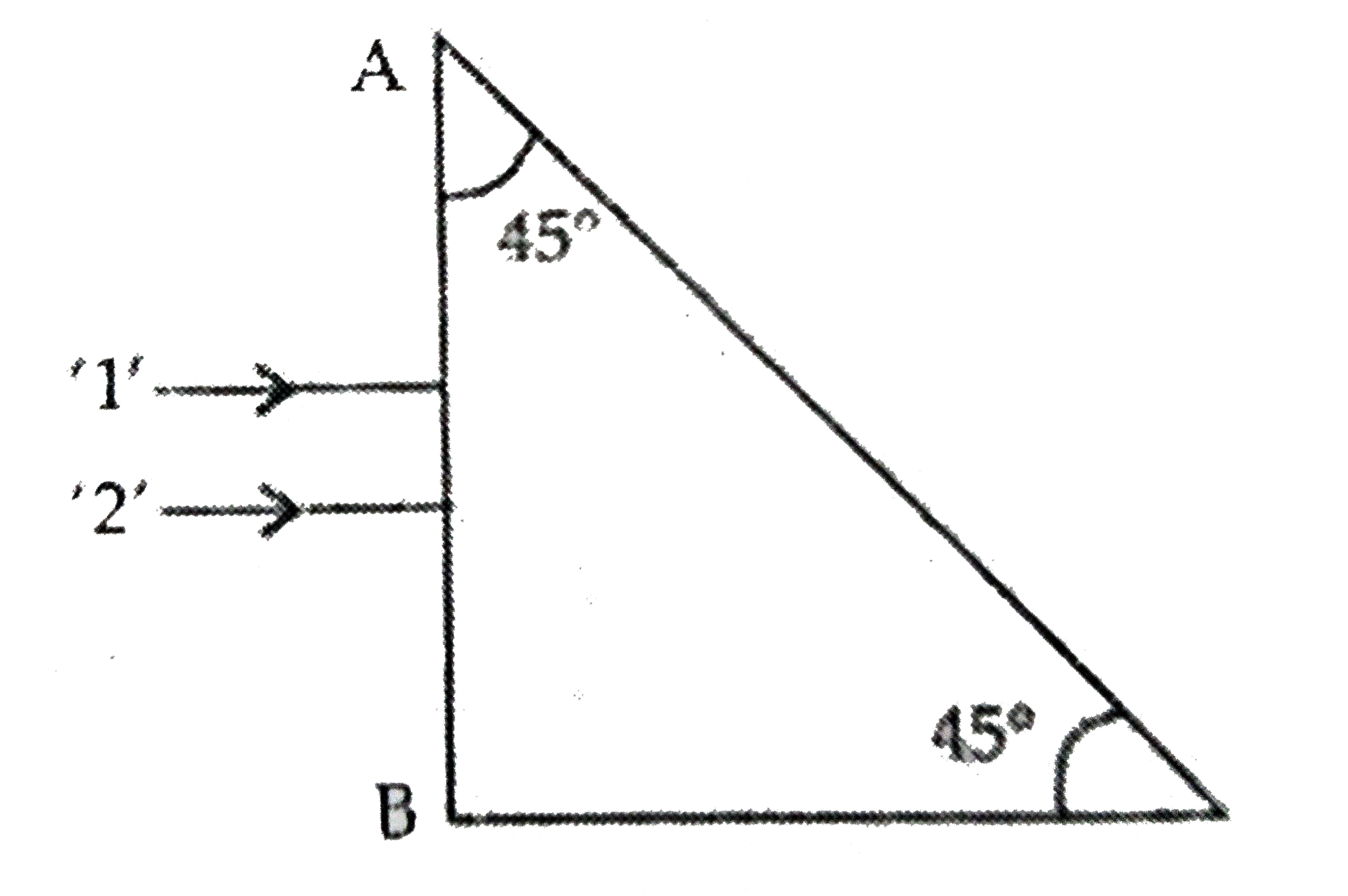
View SolutionTwo monochromatic ray of light are incident normally on the face AB of an isosceles right - angled 'I' and '2' are respectively 1.35 and 1.45. Trace path of these rays after entering through the prism.
View SolutionTwo parallel plane-polarized beams of light of equal intesity whose oscillation planes N1 and N2 from a small angle φ between them (Fig.) fall on a Nicol prism. To equalize the intensities of the beams emerging behind the prism, its principle direction N must be aligned along the bisecting line A or B. find the value of the angle φ at which the rotation of the Nicol prism through a small angle δφ<<φ from the position A results in the fractional change of intensities of the beams ΔI/I by the value η=100 times exceeding that resulting due to rotation through the same angle from the position B.
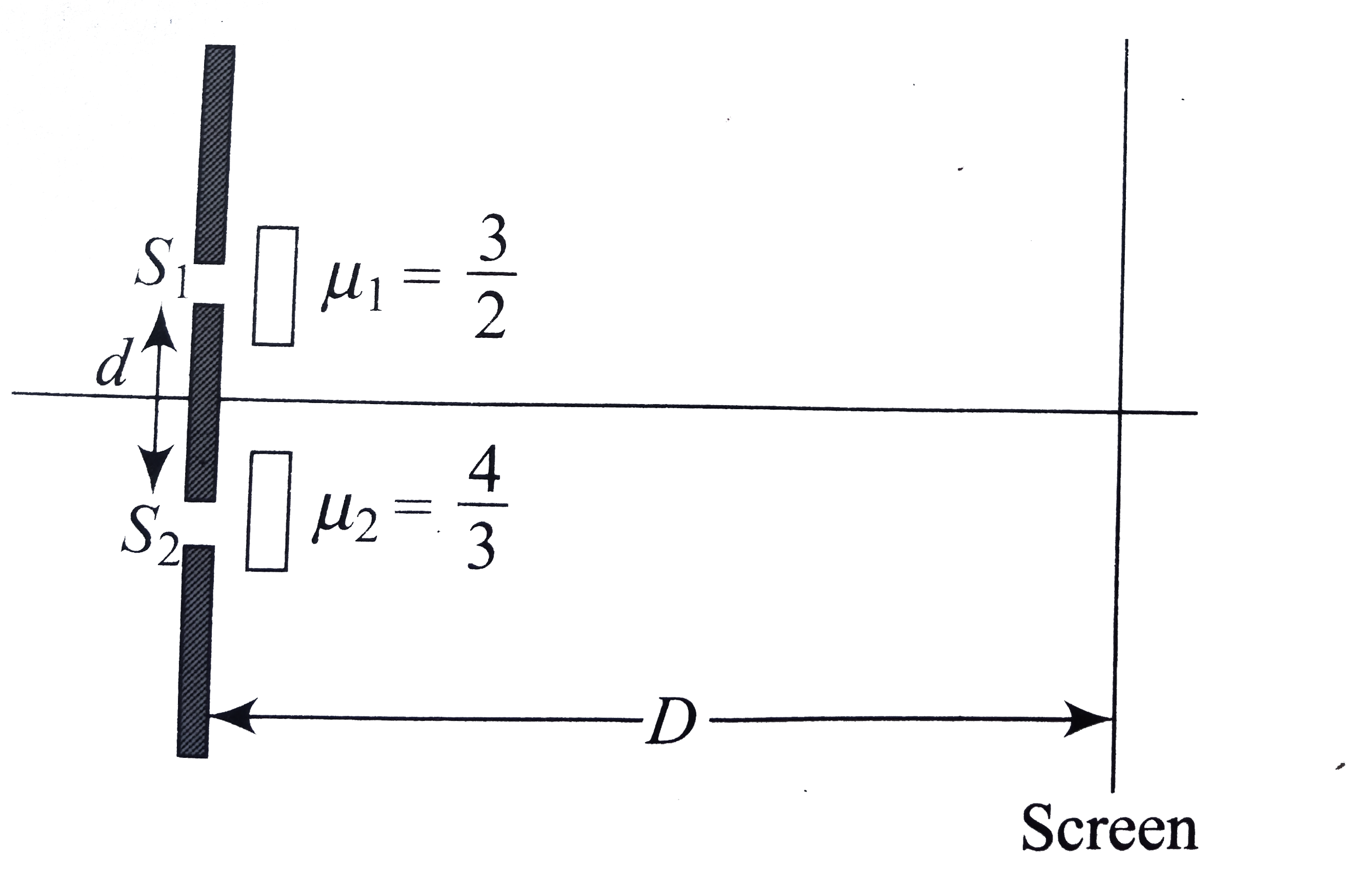
View SolutionA monochromatic beam of light of 6000 Å is used in YDSE set-up. The two slits are covered with two thin films of equal thickness t but of different refractive indices as shown in figure. Considering the intensity of the incident beam on the slits to be I0, find the point on the screen at which intensity is I0 and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.) Consider t=6μm,d=1mm, and D=1m, where d and D have their usual meaning. Give your answer in mm.
View Solution