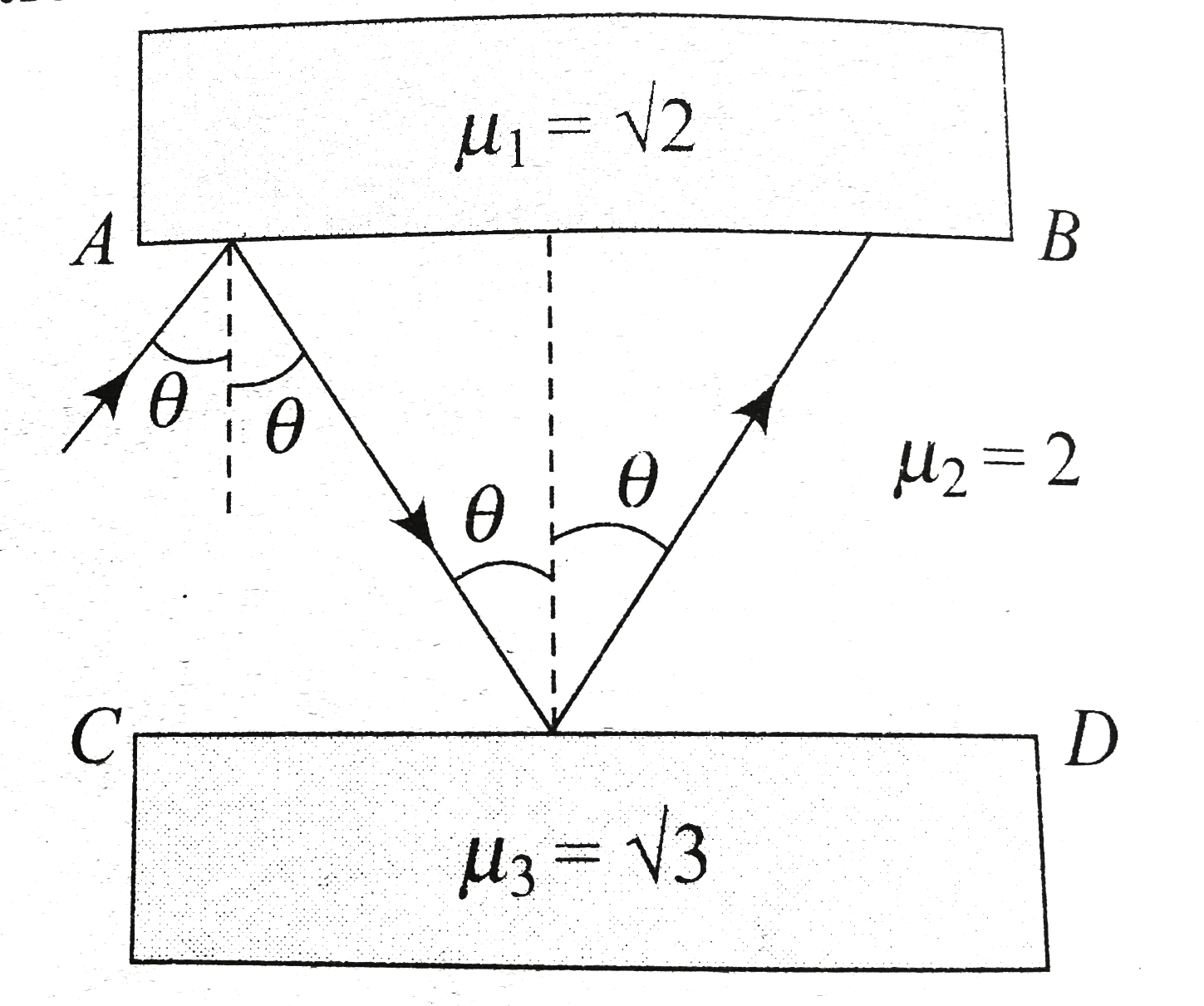
AB and CD are surfaces ot two slabs as shown in Figure . The medium between the slabs has refractive indes 2. Refractive indes of the slab above Ab is √2 and below CD is √3 . Find the minimum angle of incidence at Q, so that the ray is totally reflected by both the slabs.

Let θ be the angle of incidence at face AB, then for total internal reflection at face AB
sinθ>C1=μ1μ2=√22
⇒sinθ>1√2 or sinθ>sin45∘⇒θ<45∘
(i) For total internal reflection at face CD,
sinθ>sinC2=μ3μ2=√32⇒sinθ>√32
or sinθ>sin60∘ or θ>60∘
(ii) Therefore, the total internal reflection at both the surfaces,
θmin=60∘ .
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.2
Explore 20 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Integer Type
Explore 4 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
AB and CD are surfaces of two slabs as shown in figure. The medium between the slabs has refractive index 2, refractive index of slab above AB is √2 and below CD is √3. Find the minimum angle of incidence, so that the ray is totally reflected by both the slabs.

View SolutionAB and CD are two slabs. The medium between the slabs has refractive index 2 . Find the minium angle of incidence of Q , so that the ray is totally reflected by both the slabs .
_E01_252_Q01.png)
View Solution
Knowledge Check
Refractive index of a rectangular glass slab is μ=√3. Alight ray incident at an angle 60° is displaced laterally through 2.5 cm. Distance travelled by light in the slab is
A4 cm/s towards the mirrorB5cmC2.5√3 cmD3cmA rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
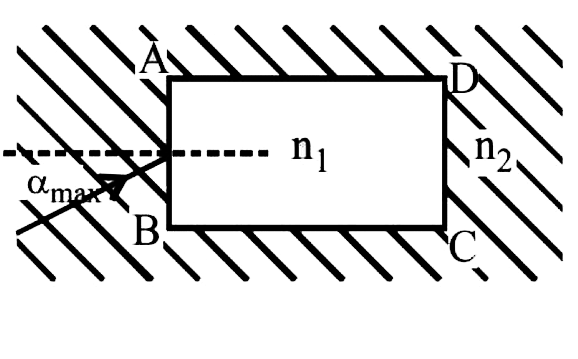 Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
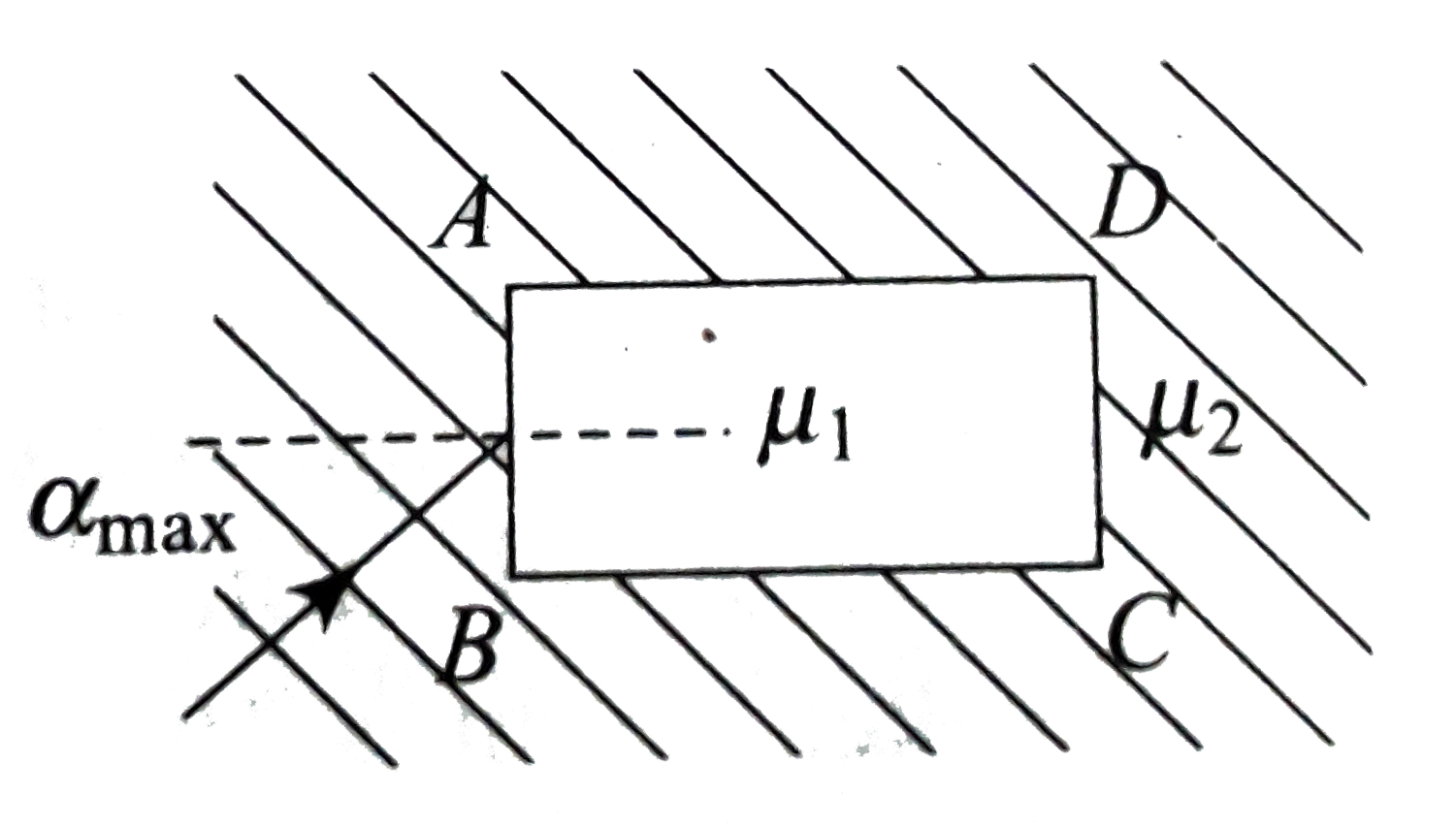 Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
A prism of refractive index √2 has refractive angle 60∘ . Find the angle of incidence so that a ray minimum deviation.
View SolutionA rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
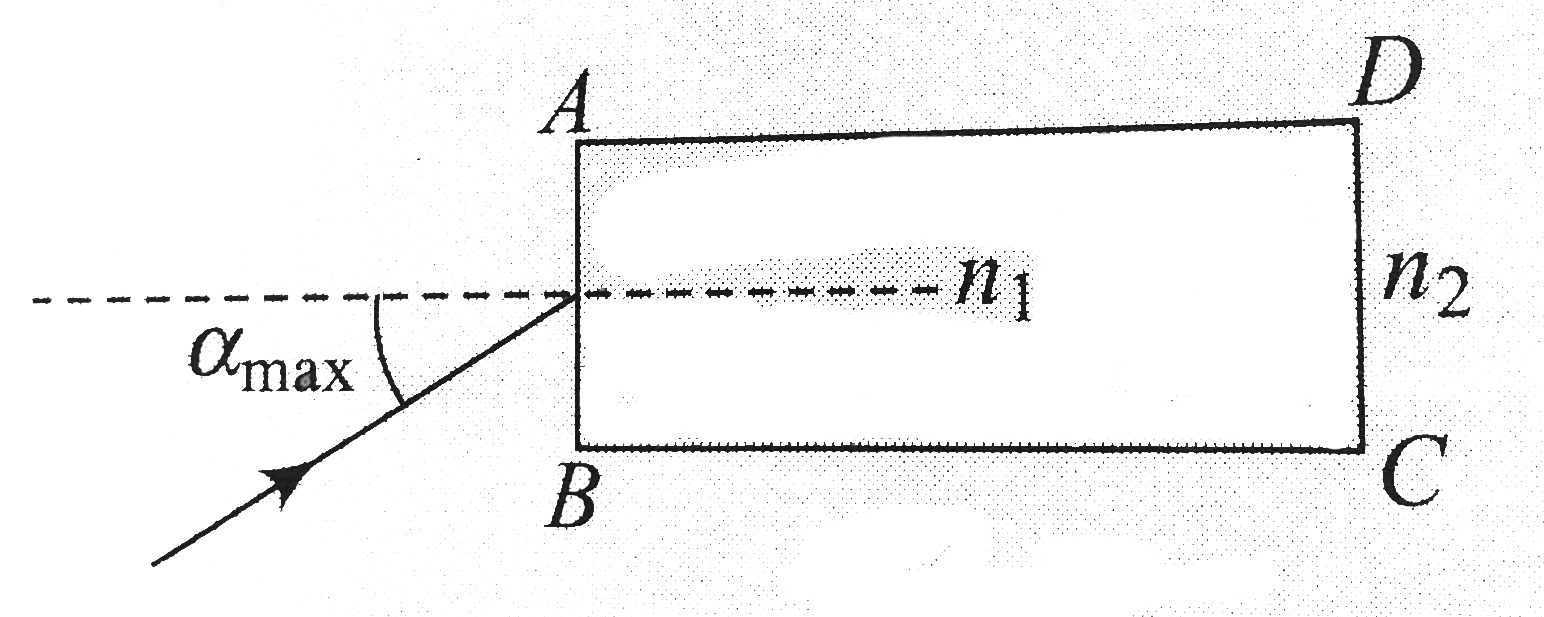
View SolutionOne side of a glass slab is silvered as shown in the figure. A ray of light is incident on the other side at angle of incidence 45∘. Refractive index of glass is given as √2. The deflection suffered by the ray when it comes out of the slab is
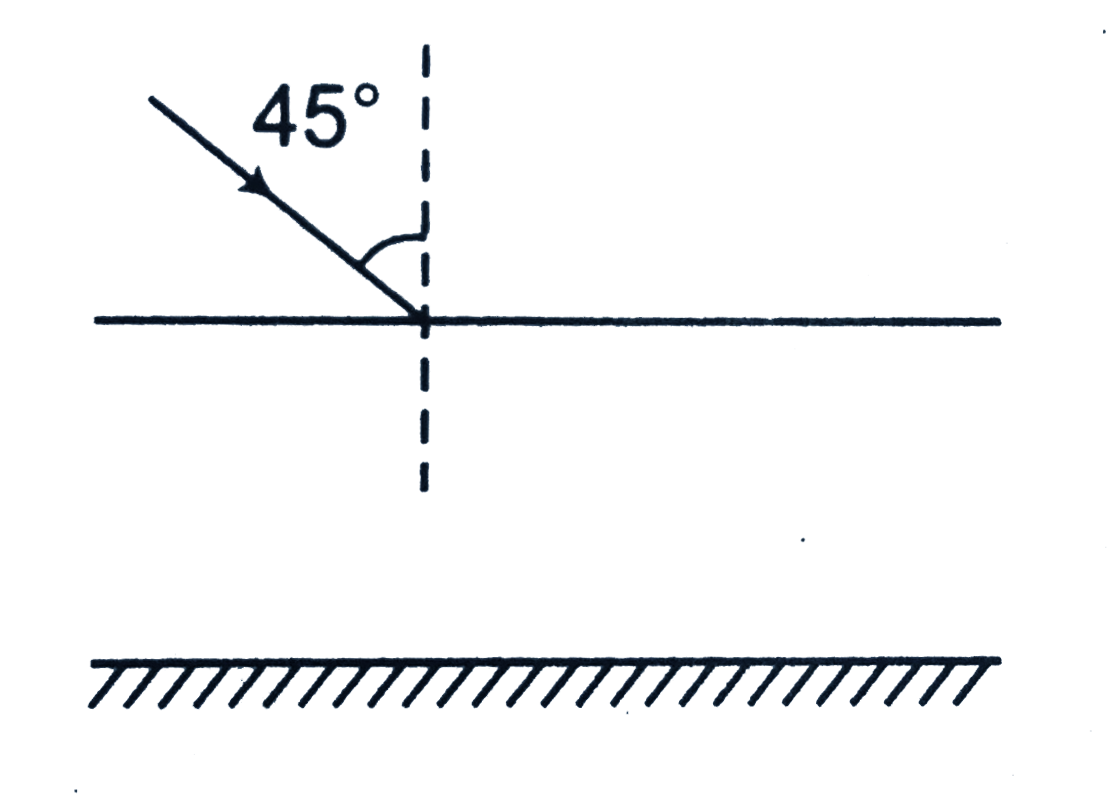
View SolutionA ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
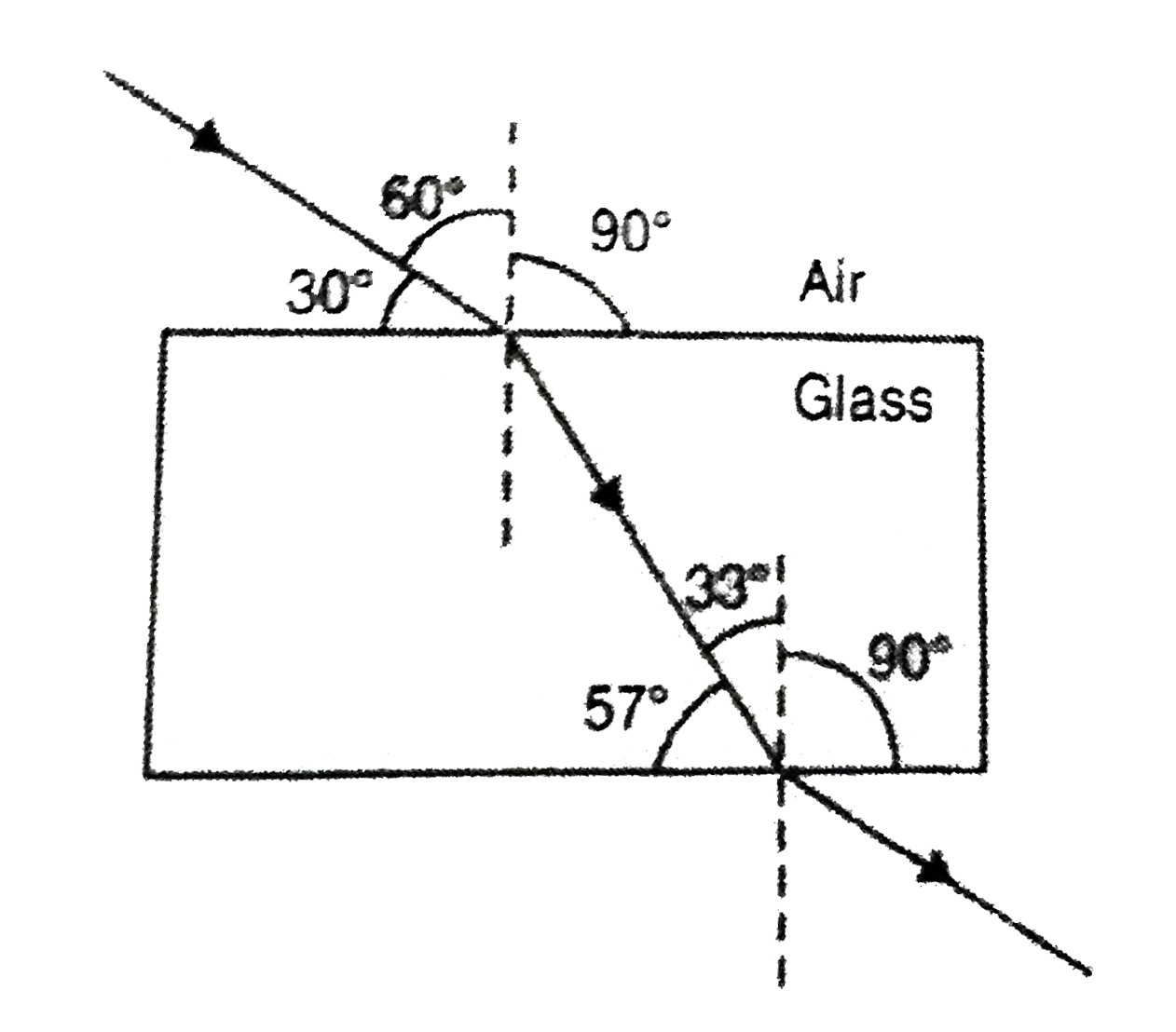
View SolutionA rectangular glass slab ABCD of refractive index n1 is immerged in water of refractive index n2(n1>n2) . A ray of light is incident at the surface AB of the slab as shown . The maximum value of the angle of incidence αmax , such that the ray comes out only from the other surface CD , is given by :-
_E01_205_Q01.png)
View Solution

