Consider 12 resistor arranged symmetrically in shape of bipyraimd ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the planw of squar. The resistacne of each resistor is R. 
The effective resistance between A and C is
R/2
R/3
R
none of these
The correct Answer is:A
If we cannot battery between E and F, then A, B, C, and D will be
all at the same potential. Req=R4+R4=R2 
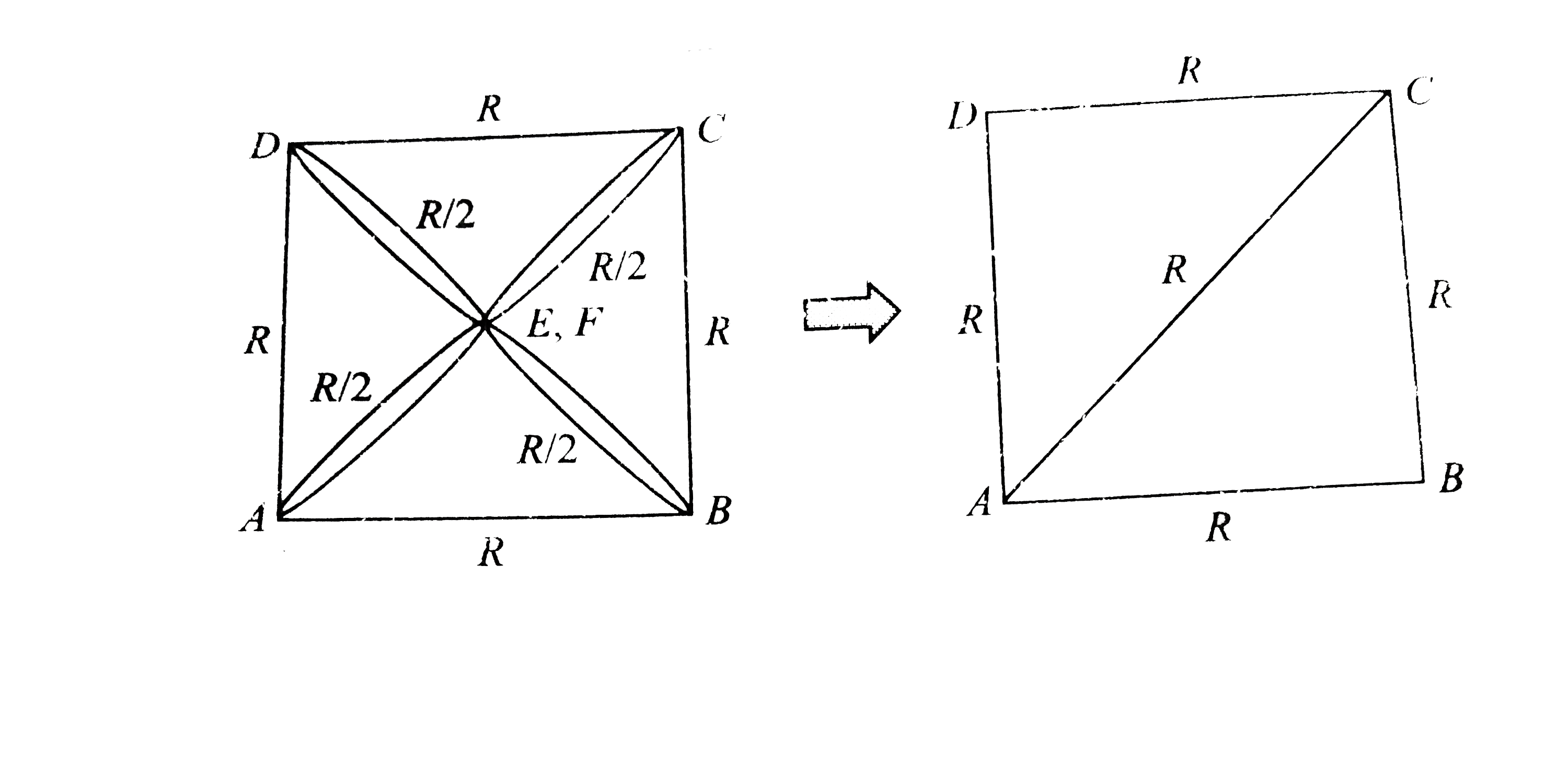
If we connect a battery
between A and C, then E and
F will be at the same potential.
 ,
, 
Now resistance between DE and EB will be useless. Thus,
Req=R/2
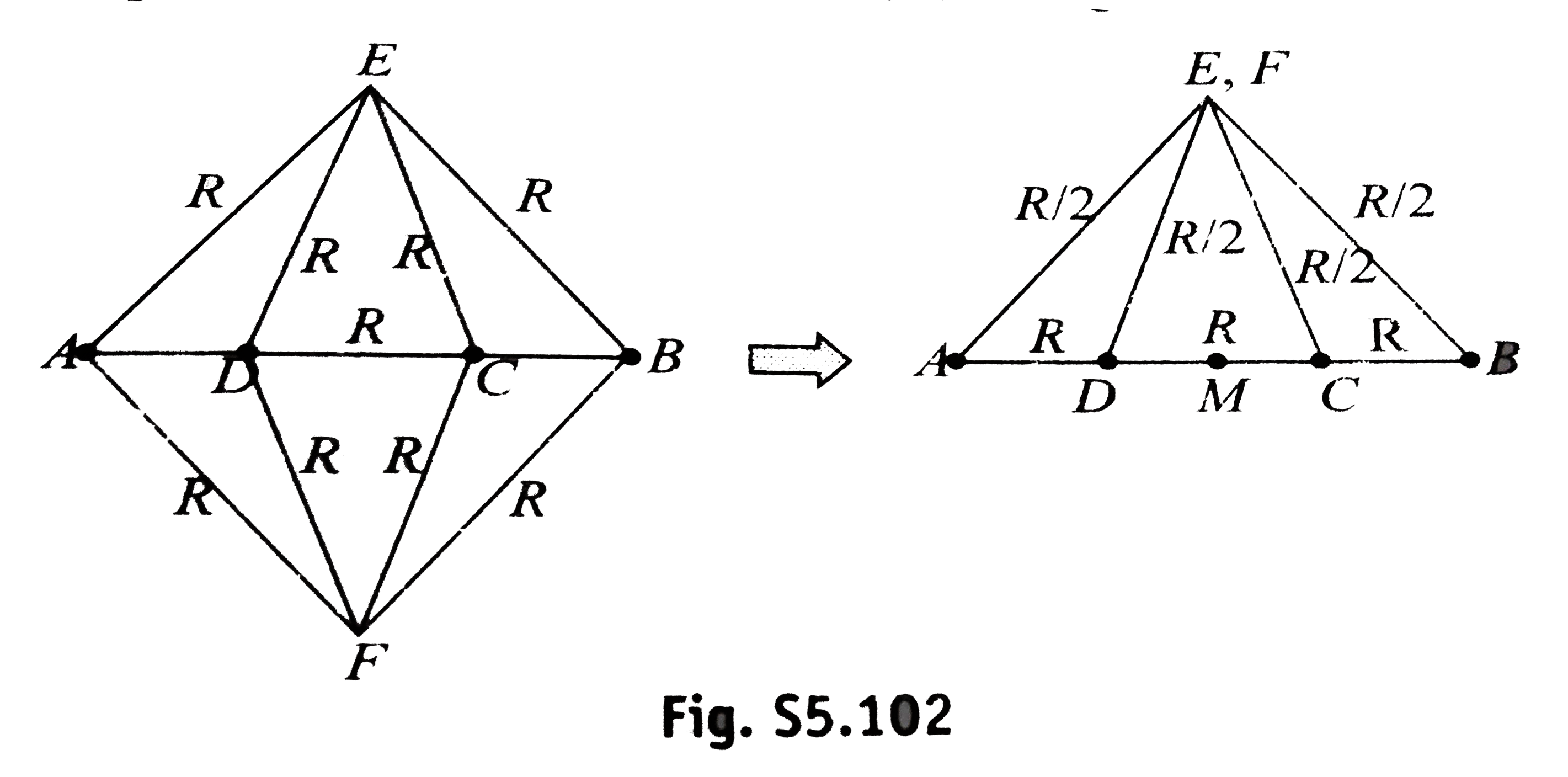
Let us remove the resistance between A and B, then E and F will be at
the same potential, we can draw the remaining as follows:
 ,
,
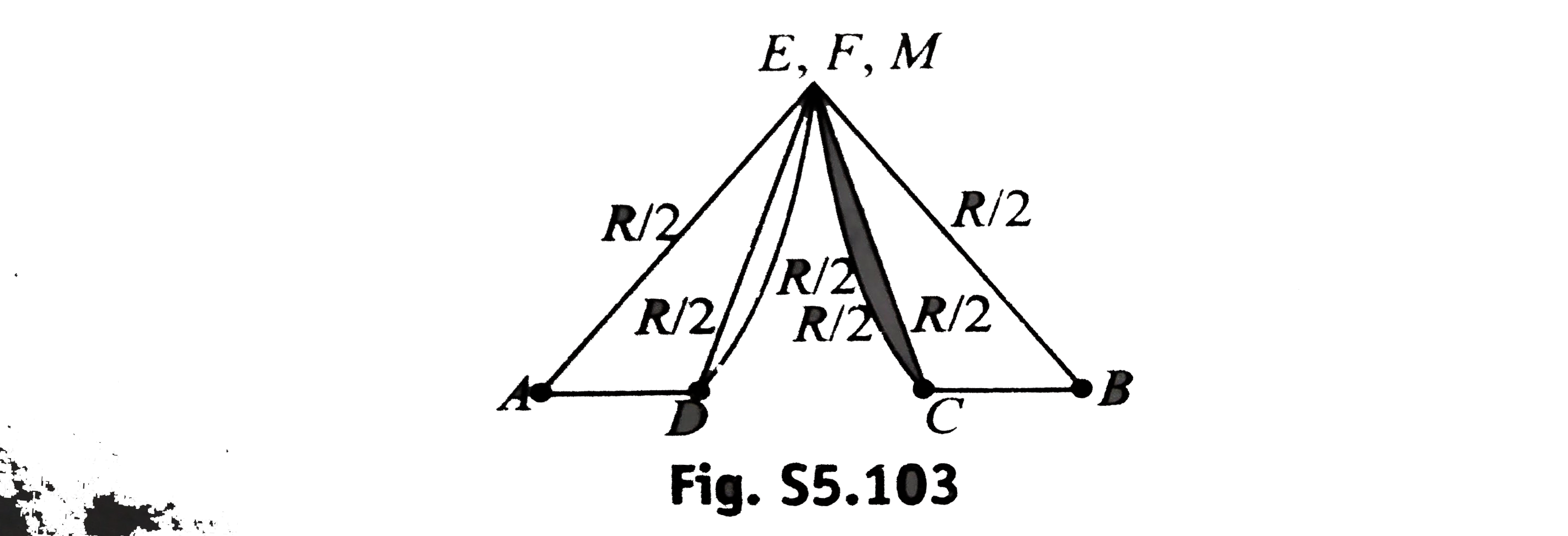
M is the midpoint of DC, so M will be at the same spot as E and F.
Now find RAB=5/7R. The resistance that we had removed will be in
parallel to it, so
Req=RABRRAB+R=(5/7)RR(5/7)R+R=512R
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
A wire of resistance R is bent to form a square ABCD as shown in the figure. The effective resistance between E and C is: (E is mid-point of arm CD)

View SolutionFour identical positive point charges Q are fixed at the four corners of a square of side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large distance along the line perpendicular to plane of square. The minimum value of initial velocity v0 (in m/s) required to cross the square is ?
(m=1gm,l=4√2m,Q=1μc,q=0.5μc)

View Solution
Knowledge Check
Consider 12 resistor arranged symmetrically in shape of bipyraimd ABCDEF. Here ABCD is a square. Point E, point F, and centre of square are in the same straight line perpendicular to the planw of squar. The resistacne of each resistor is R.

The effective resistance between E and F isAR/2BR/3CRDnone of theseIn the shown wire frame, each side of a square (the smallest square) has a resistance R. The equivalent resistance of the circuit between the points A and B is
 ARB2RC4RD8R
ARB2RC4RD8R_2019_CBT3_E01_033_Q01.png)
A wire of length l and resistance R is bent in form of square form of square as shown in figure. If E is a mid point of side D,A, then equivalent resistance between points E& A is:A7R64B7R32C7R16D7R8
It is desired to make a 20Omega coil of wire which has a zero thermal coefficient of resistance. To do this, a carbon resistor of resistance R, is placed in series with an iron resistor of resistance R. The proportions of Iron and carbon are so chosen that R1,+R2=20Ω for all temperatures near20∘C. How large are Ri andR2 ? (a−(c)=−0.5×10−3/∘C,afe=5×10−3/∘C)
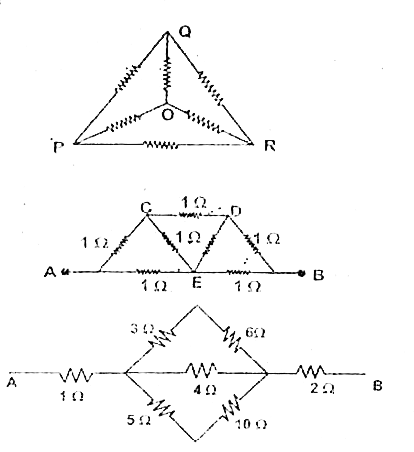
(b) Six equal resistances, each of resistance4Ω are connected to form the following figure. What is the resistance between any two corners?
(c) In the network shown in figuro, each resistance is 1Ω. What is the effective resistance between A and B.
(d) Find the equivalent resistance between points A and B of the network shown in the given diagram.
View SolutionA current carrying conductor is in the shape of an arc of a circle of radius R subtending an angle q at the centre (C). A long current carrying wire is perpendicular to the plane of the arc and is at a distance 2R from the midpoint (M) of the arc on the line joining the points M and C. Current in the arc as well as straight wire is I. Find the magnetic force on the arc.

View SolutionA regular pyramid of square is made of eight identical wires each resistance 12Ω shown in the figure. The terminals A and B are the mid-point of the corresponding sides. Find equivalent resistances between the terminals A and B in ohms.
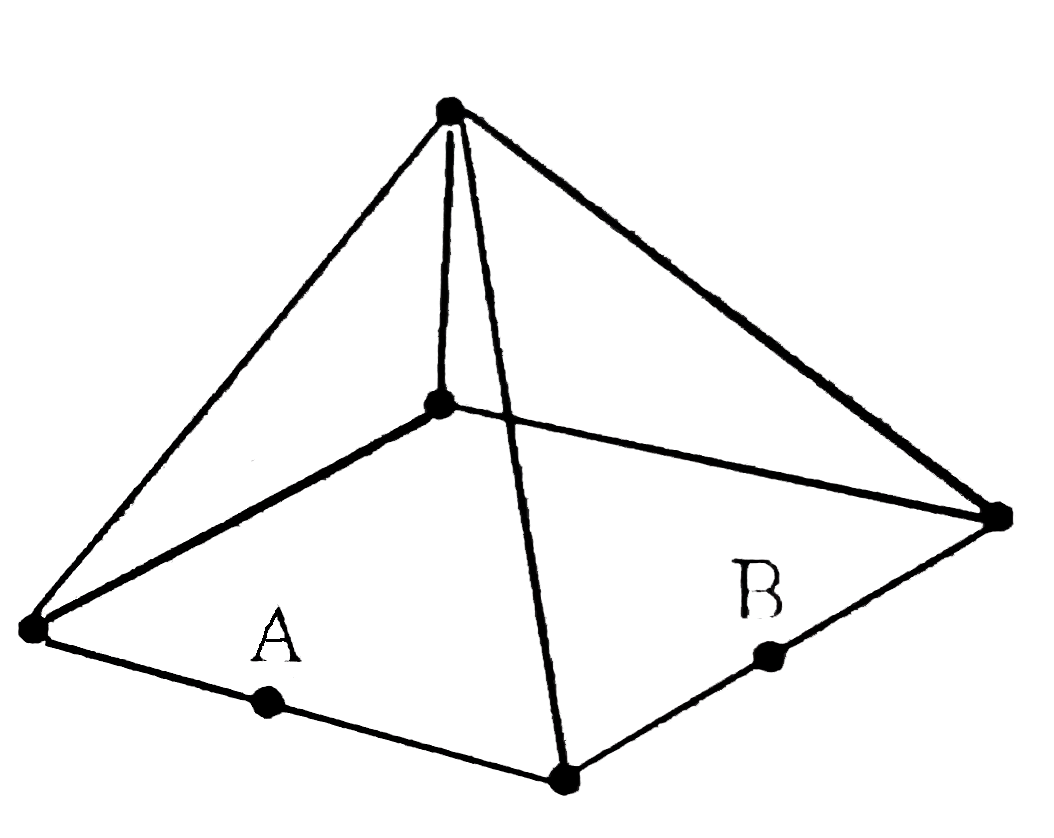
View SolutionThe equivalent resistance between the points A and B is (R is the resistance of each side of smaller square)

View SolutionTwo identical short bar magnets, each having magnetic moment of 10Am2, are arranged such that their axial lines are perpendicular to each other and their centres be along the same straigh line in a horizonetal plane. If the distance between their centres is 0.2m, the resultant magnetic induction at a point midway between them is
(μ0=4π×10−7Hm−1)
View Solution
