A network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.
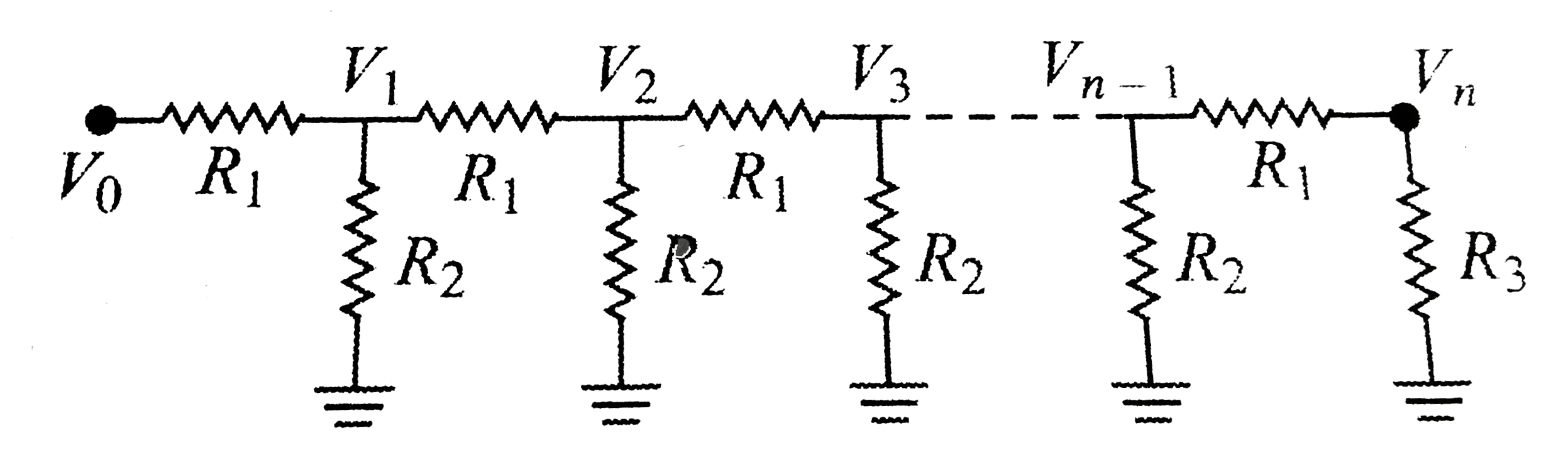
The ratio R2/R3 is
(k−1)2k
k2−1k
kk−1
k−1k2
The correct Answer is:C
Given V1=V0k,V2=V1k,V3=V2k,I=I1+I2
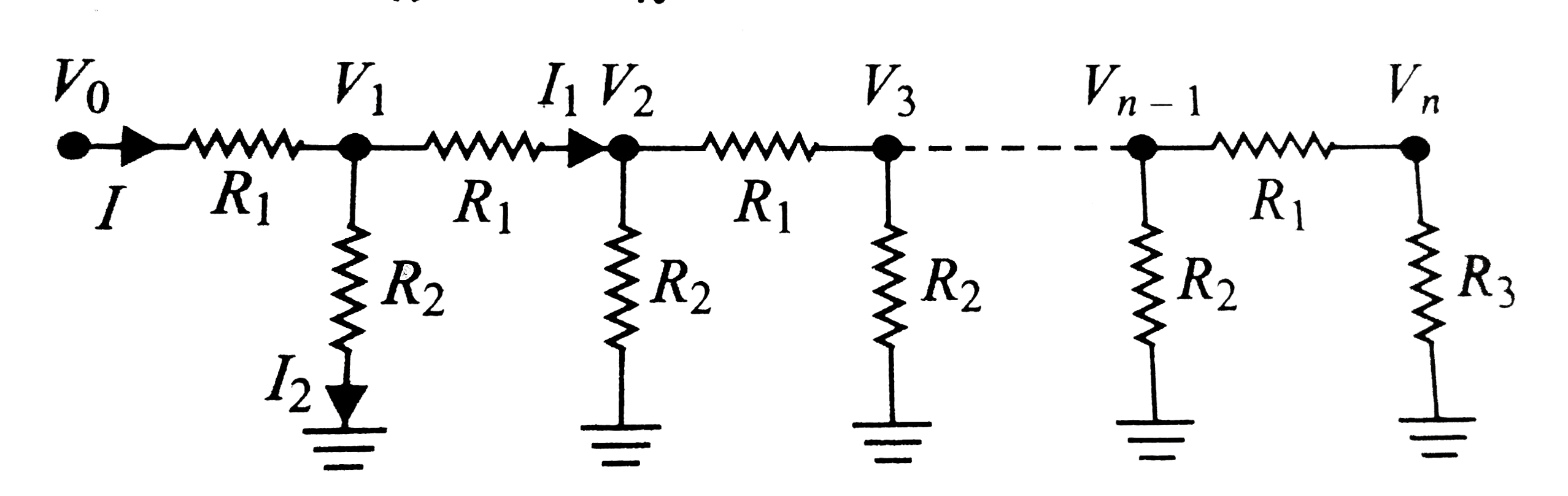
V0−V1R1=V1−V2R1+V1−0R2
V0−V1/kR1=V0/k−V0/k2R1+V0/kR2
R1R2=(k−1)2k
current in R1 and R3 will be the same:
Vn−1−VnR1=VnR3
or Vn−1−Vn−1kR1=Vn−1kR3
or R1=R3(k−1)
put the value of R1 in the above expression, we get
R2R3=kk−1
Current in R2 nearest to V0 is
I2=V1R2=V0/kR3(kk−1)=(k−1K2)V0R3
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct
16 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
A network of resistance is constructed with R1&R2 as shown in the figure . The potential at the points 1,2,3 ,,,,, N and V1,V2,V3,,,,,,,Vn respectively each having a potential k time smaller than previous one. Find
R1R2andR2R3 in terms of k
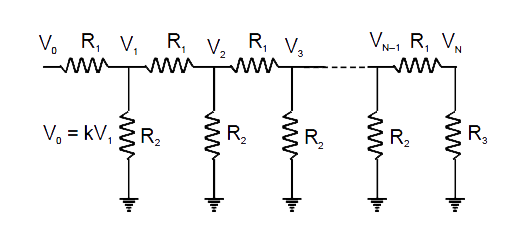
View SolutionA network of resistance is constructed with R_(1)&R_(2)asshown∈thefigure.Thepotentialatthep∮s1,2,3,,,,,NandV_(1),V_(2),V_(3) ,,,,,,, V_(n)respectivelyeachhav∈gapotentialktimesmal≤rthanpreviouso≠.F∈d<br>currenttˆpassesthroughtheresistanceR_(2)≠arest→theV_(0)∈termsV_(0),k&R_(3).
View Solution
Knowledge Check
A network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.
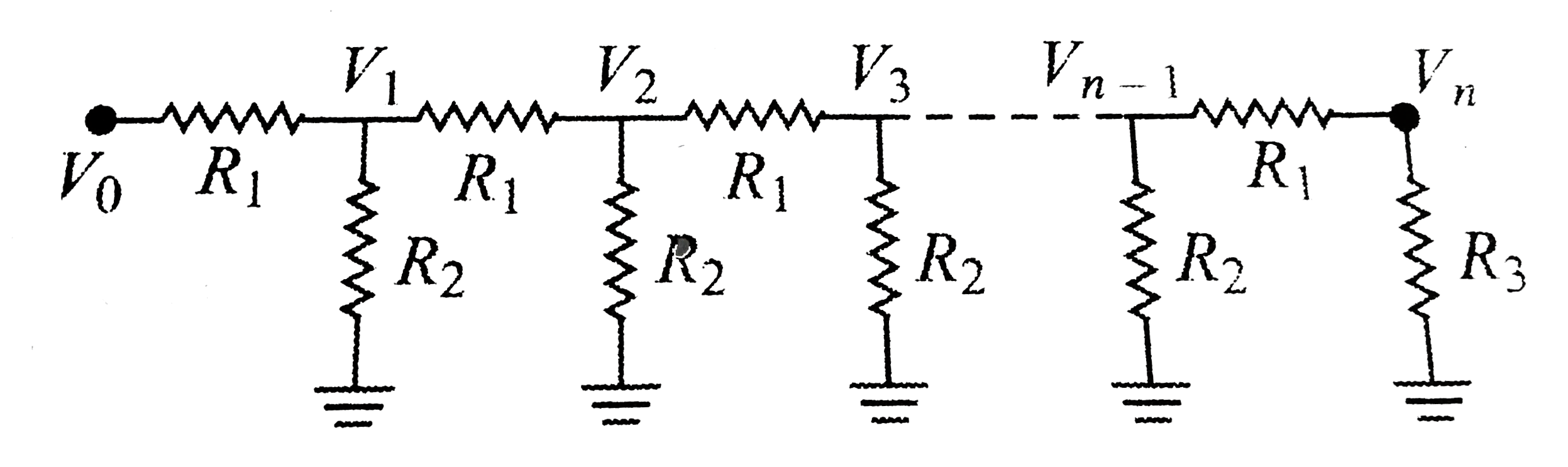
The ratio R1/R2 isAK2−1kBkk−1Ck−1k2D(k−1)2kA network of resistance is constructed with R1andR2 as shown in fig. The potential at the points 1,2,3 …., N are V1,V2,V3,…,Vn, respectively, each having a potential k times smaller then the previous one.

The current that passes through the resistance R2 nearest to the V0 isA(k−1)2kV0R3B(k+1)2k=v0R3C(k+1k2)V0R3D(k−1k2)V0R3A network of resistance is constructed with R1andR2 as shown in the figure. The potential at the points 1, 2, 3,………., N are V1,V2,V3,……..,Vn respectively each havig a potential K time smaller than privious one. Find :
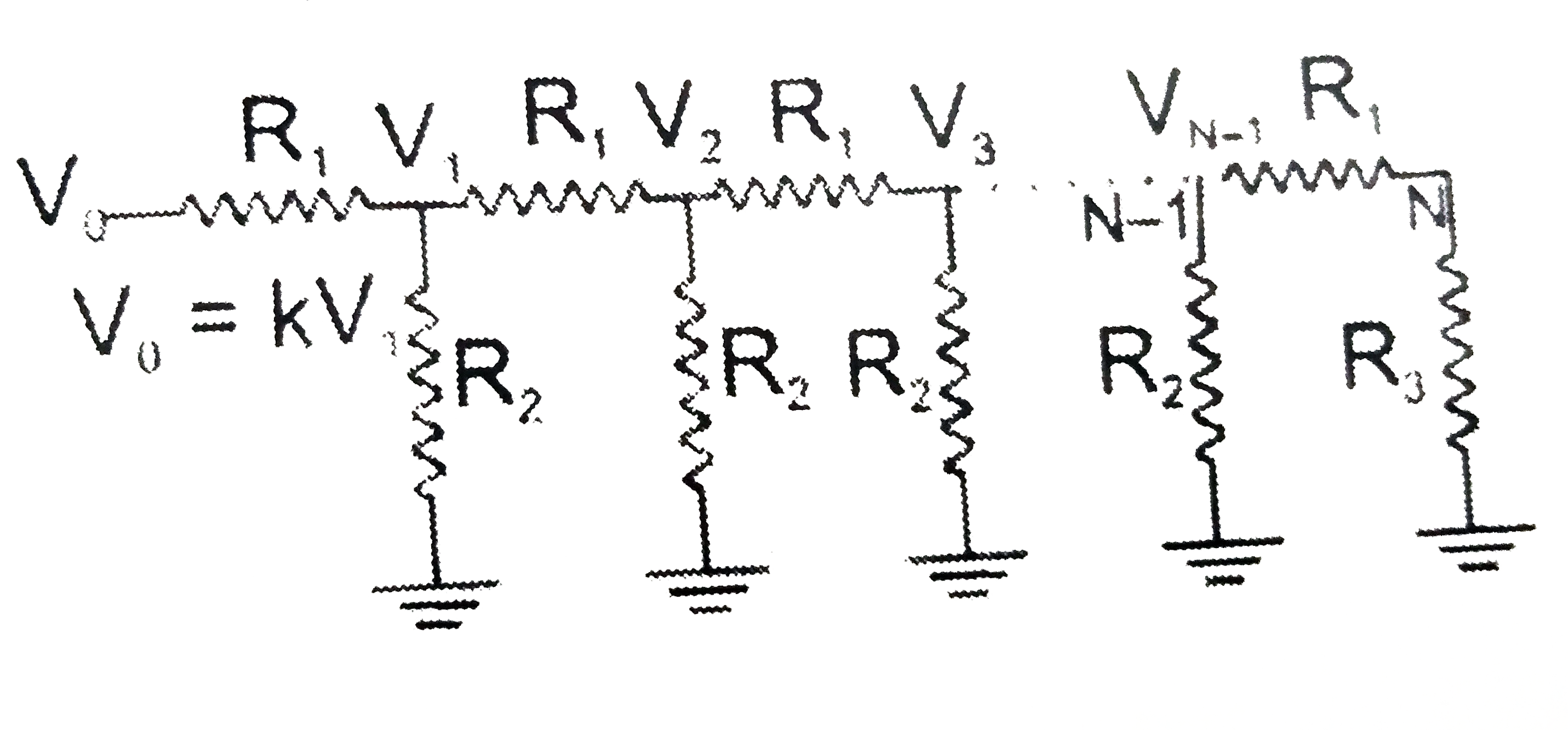
(R1R2)×(R2R3) in terms of K.AK-1BK2−1C1K+1DK−1K+1
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
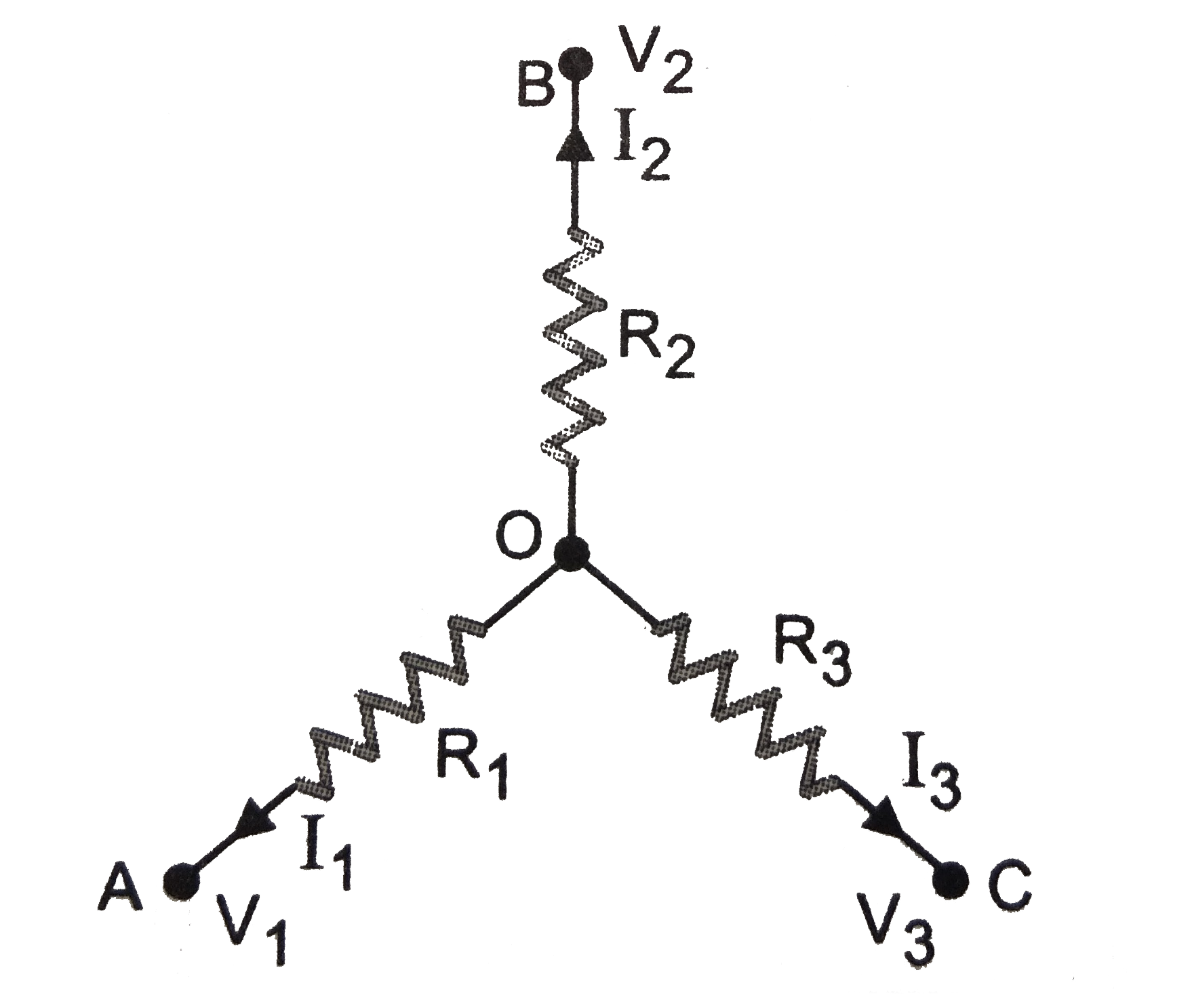
View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View SolutionThree uncharged capacitors of capacities C1,C2 and C3 are connected as shown in the figure to one another and the potentials V1,V2 and V3 respectively. Then the potential at O will be
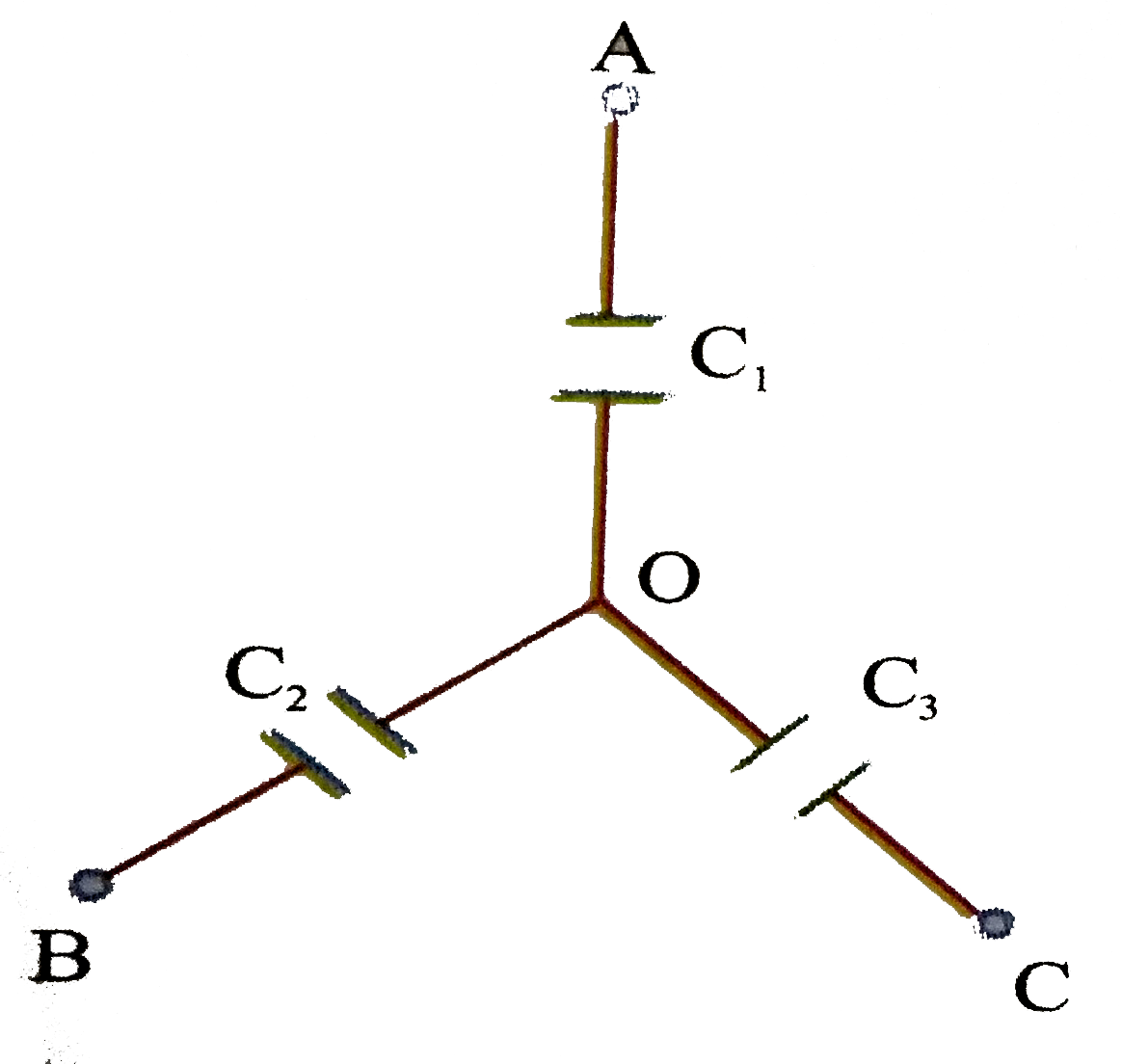 .
.
View SolutionIn the circuit as shown, it is given that R1/R2=1/2 and potential at O is V.
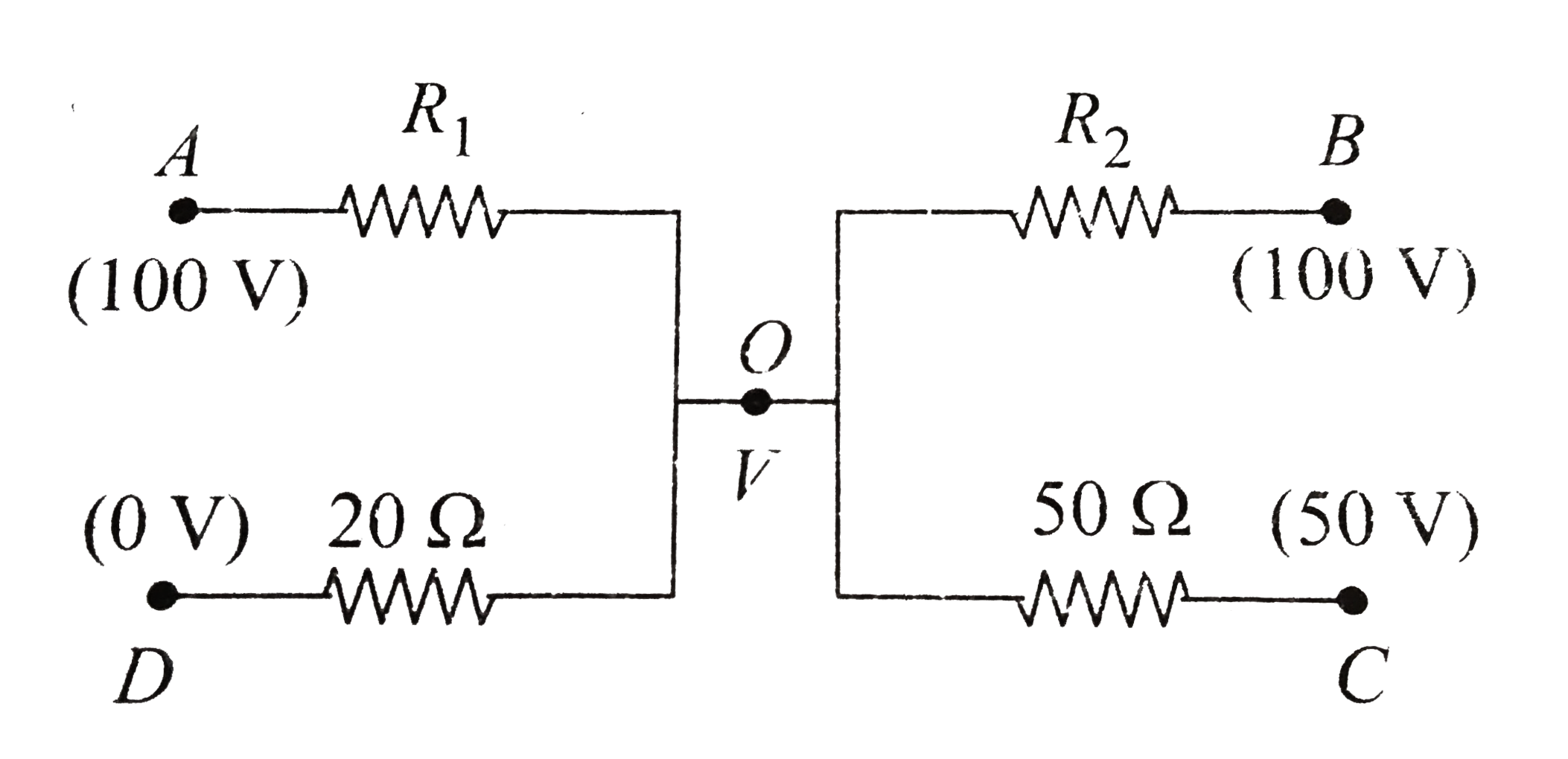
View SolutionThree planets of same density and with radii R1,R2 and R3 such that R1=2R2=3R3 have gravitation fields strength on planets are v1,v2,v3, respectively. Then :
View Solution
