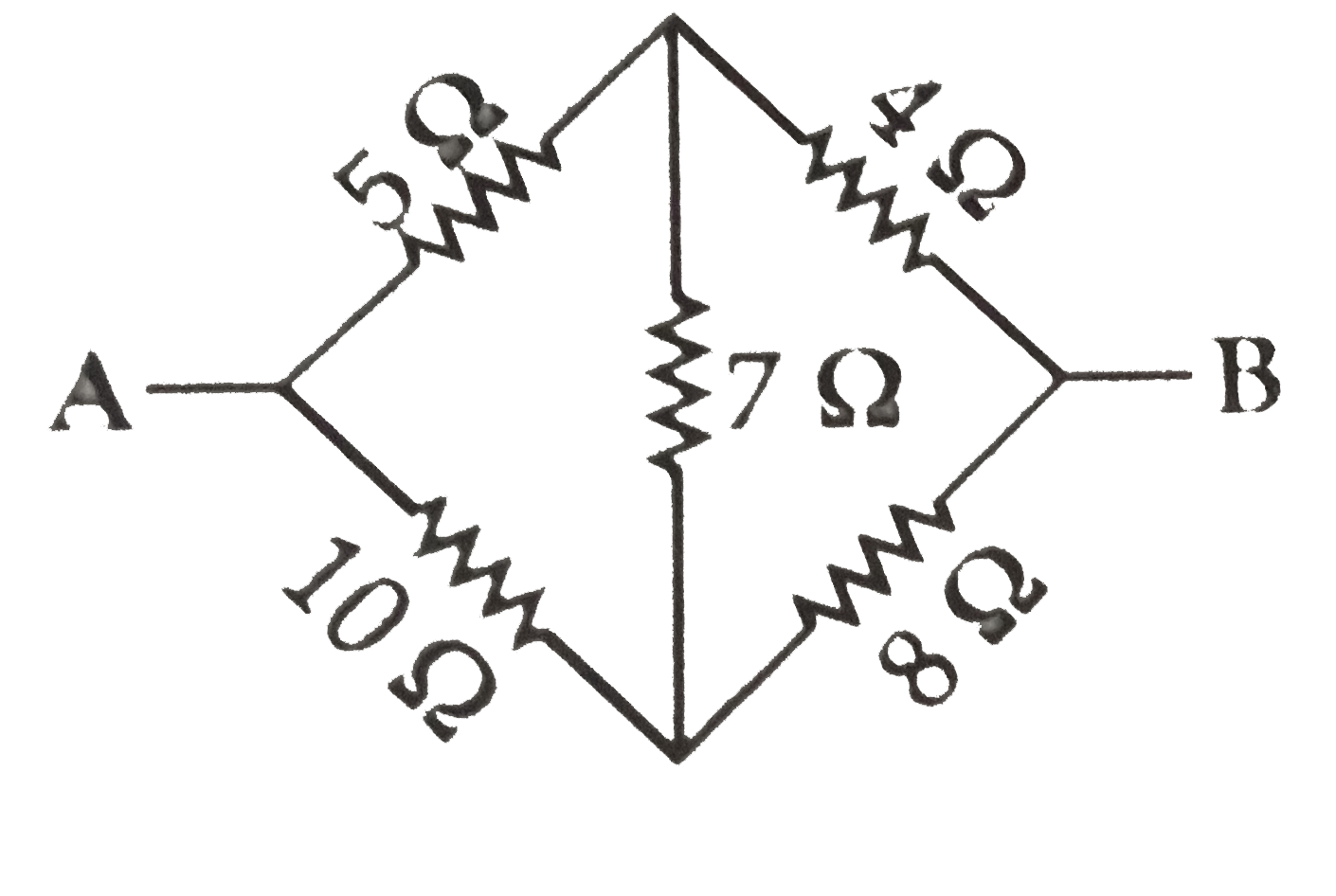
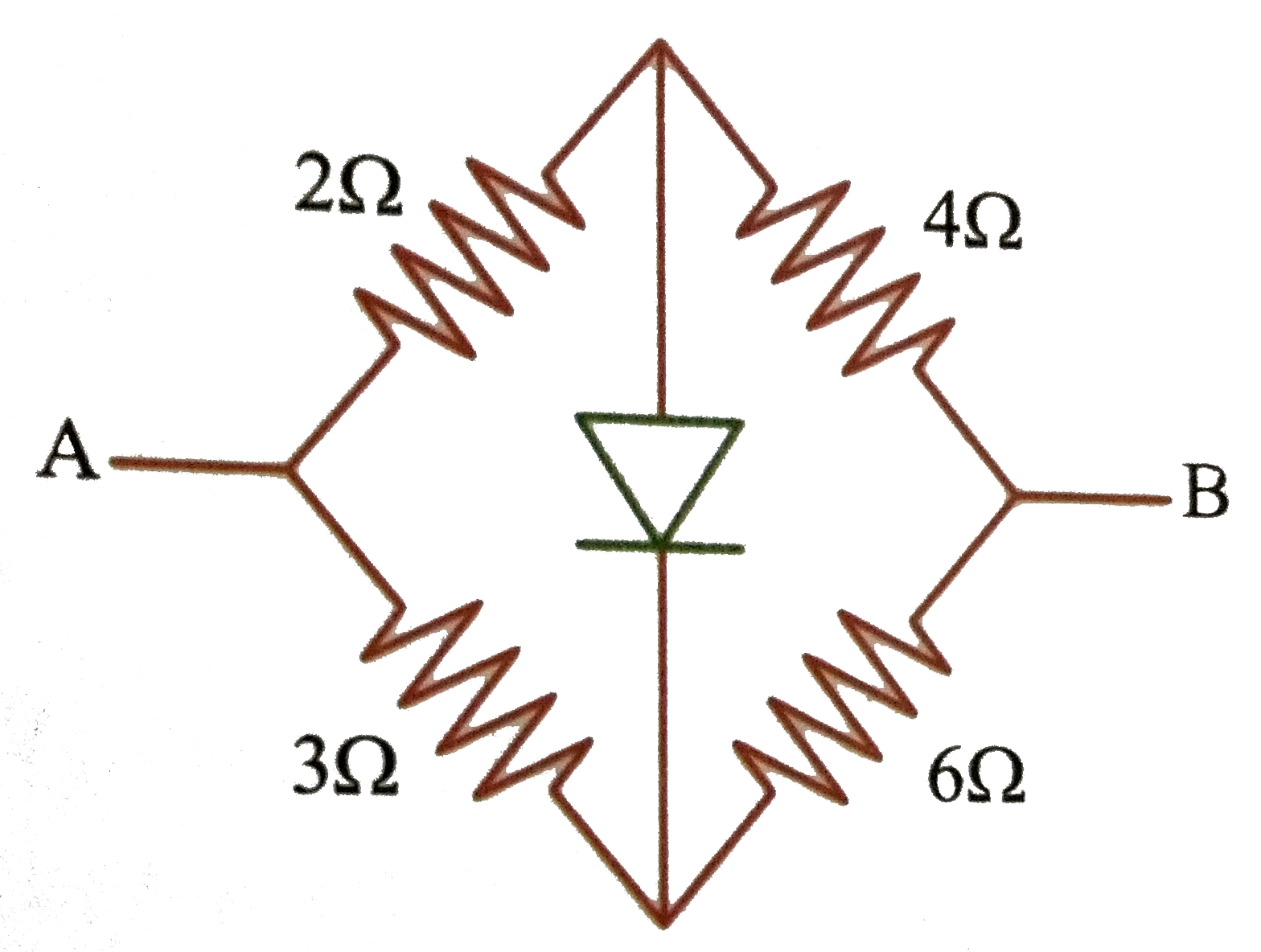
Six resistor are arranged along the edges of a pyramid as shown in Fig. 5.43. The values of resistances are mentioned with resistances in the figure. Find the effective between A and B.
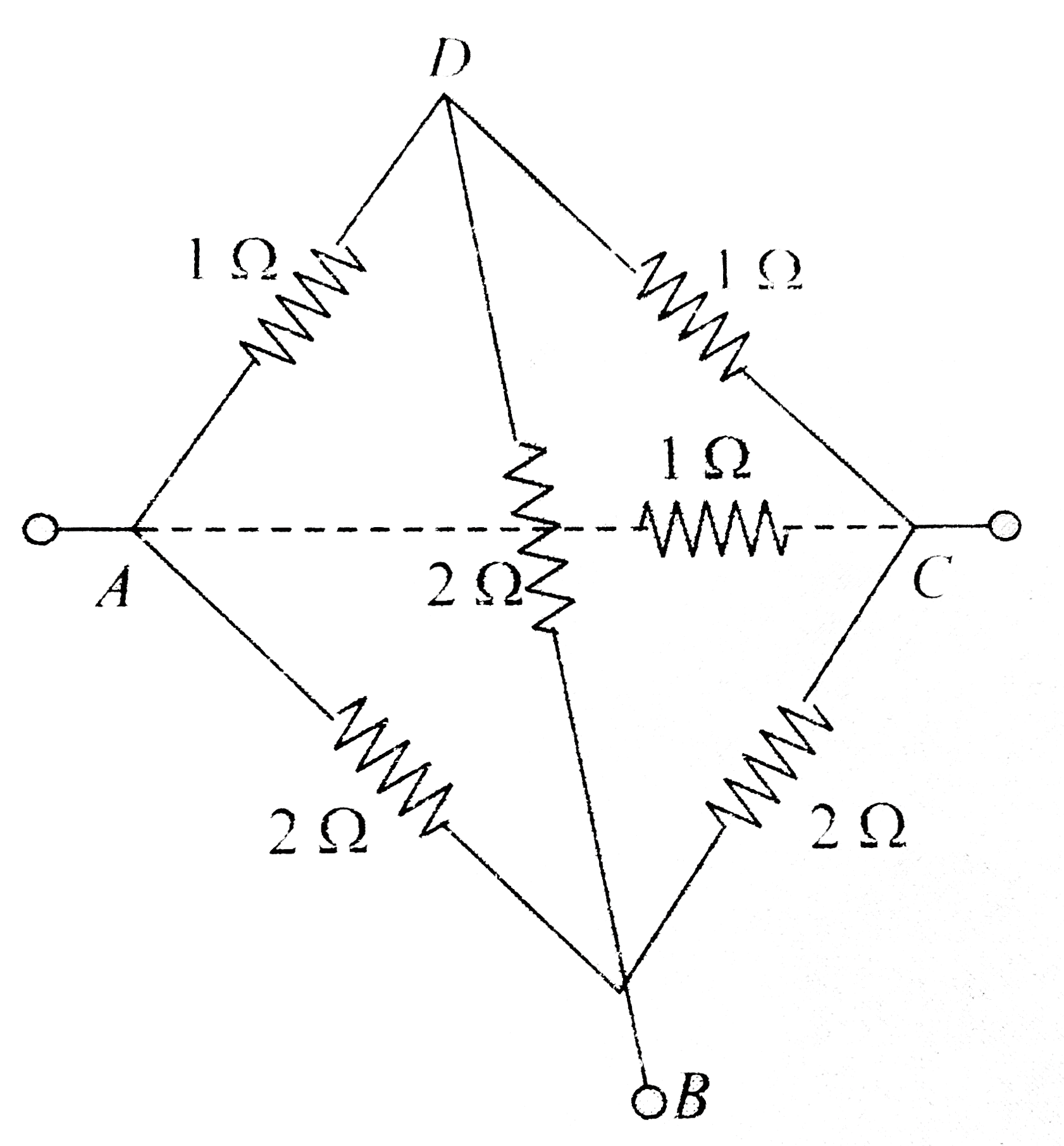
Video Solution
Text Solution
The branches ADB and ACB are symmetrical relative to the
terminals A and B. Hence, the points D and C are equipotential.
Since RDC≠0,iDC=0. Then remove the branch DC and then the
circuit is reduced to a simpler one as shown in the figure. Then

1RAB=12+12+12RAB=23Ω
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Solved Examples12videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.128videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the effective resistance between A and B.
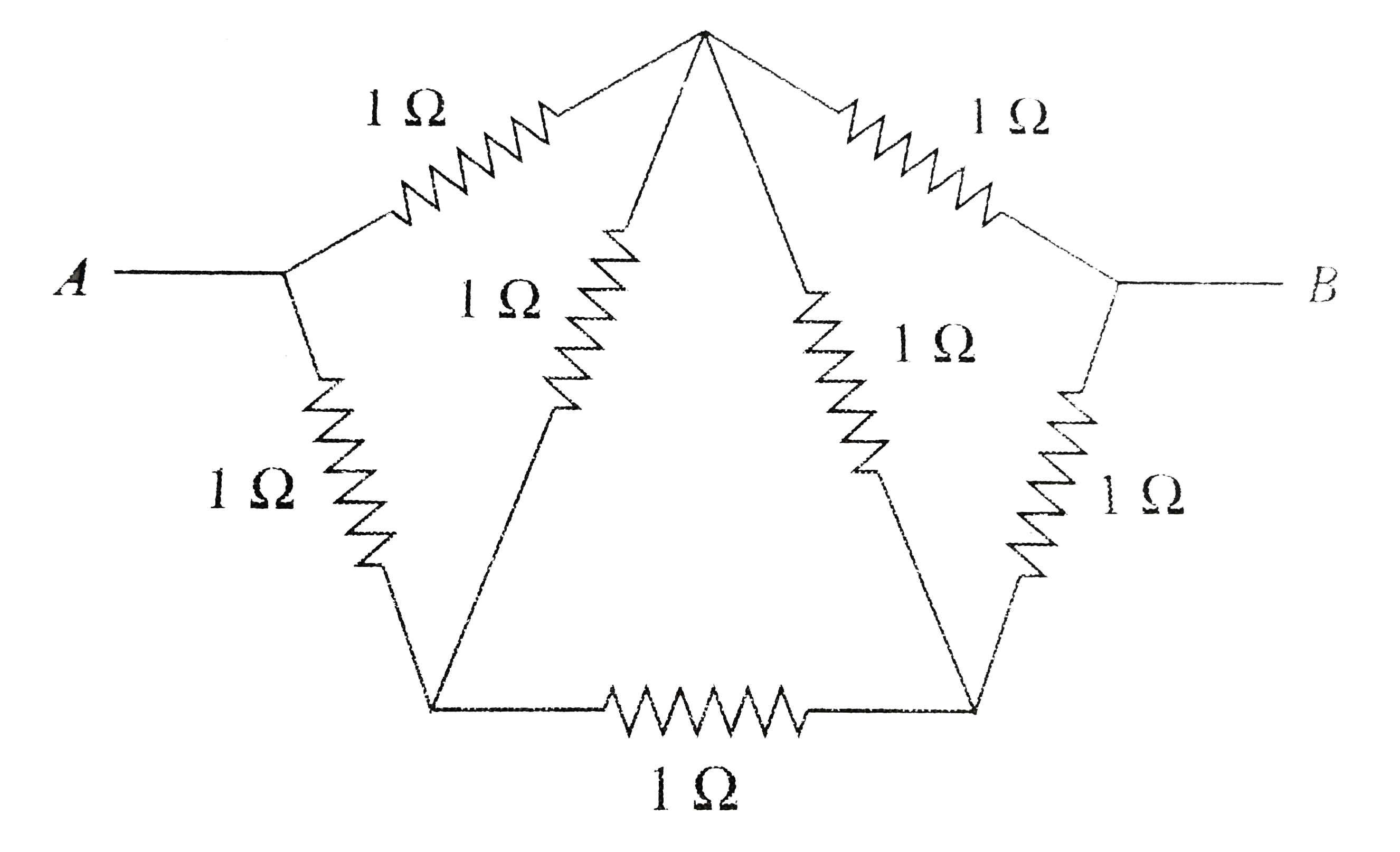 A2ΩB1ΩC8/7ΩD7Ω
A2ΩB1ΩC8/7ΩD7Ω - Question 2 - Select One
Find the effective resistance between A and B
 A5/8ΩB9/5ΩC18/5ΩD5/9Ω
A5/8ΩB9/5ΩC18/5ΩD5/9Ω - Question 3 - Select One
Find the effective resistance between A and B
 .A5/18ΩB9/5ΩC18/5ΩD5/9Ω
.A5/18ΩB9/5ΩC18/5ΩD5/9Ω
Find the effective resistance between A & B
 .View Solution
.View SolutionAB hold resistances as indicated in the figure. The effective resistance between A and B will be
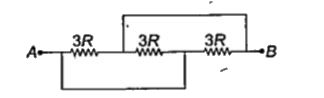 View Solution
View SolutionAB hold resistances as indicated in the figure. The effective resistance between A and B will be
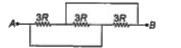 View Solution
View SolutionFind effective resistance between A & B.
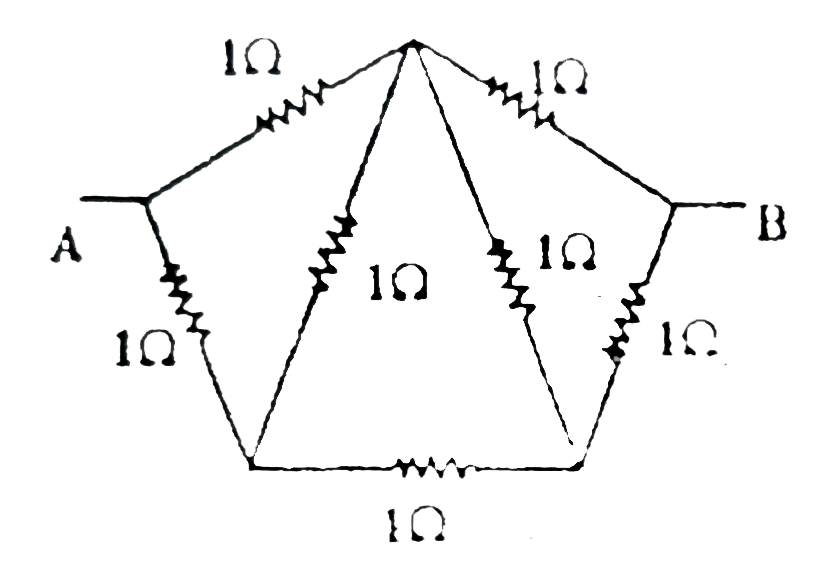 View Solution
View SolutionFive resistances are connected as shown in the figure. The effective resistance between the points A and B is
 View Solution
View Solution