Two small beads having positive charges 3q and q are fixed at the opposite ends of a horizontal, insulating rod, extending from the origein to the point x=d as shown in fig. A third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable eqyilibrium ?
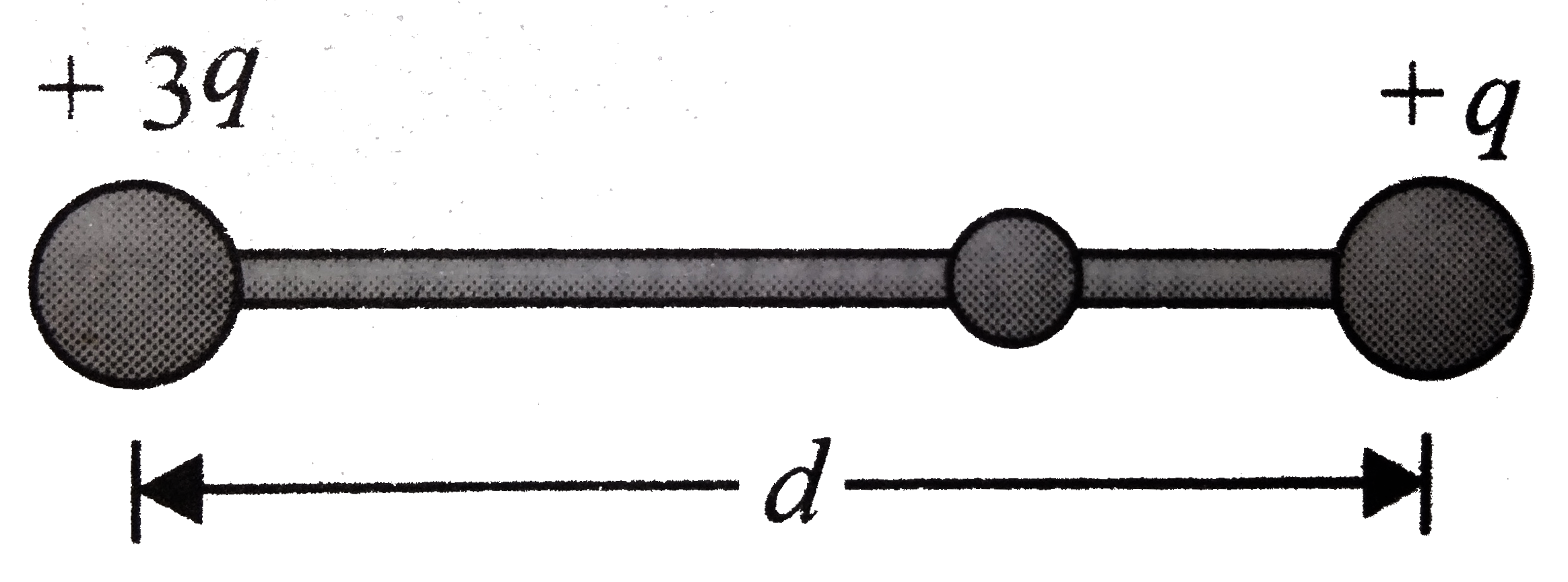
The correct Answer is:√3d√3+1

For Q to be in equilibrium
k3qQx2=kQq(d−x)2
or , x=√3d√3+1
The bead can be in stable equilibrium, if it has positive charges.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICSChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Exercises
Explore 58 Videos
- COMMUNICATION SYSTEMBook:CENGAGE PHYSICSChapter:COMMUNICATION SYSTEMExercise:QUESTION BANK
Explore 19 Videos
- Current ElectricityBook:CENGAGE PHYSICSChapter:Current ElectricityExercise:QUESTION BANK
Explore 40 Videos
Similar Questions
Two positive point charges , each Q , are fixed at separation d. A third charge q is placed in the middle. Describe the equilibrium of the third charge.
View SolutionFour small particles charged with equal positive charges Q each are arranged at the four corners of a horizontal square of side a. A unit positive charge mass m is placed at a point P, at a height h above the centre of the square. What should be the magnitude of charge Q in order that the unit charge remain in equilibrium
View Solution
Knowledge Check
In the shown figure two beads slide along a smooth horizontal rod as shown in figure. The relation between v and v0 in the shown position will be
 Av=v0cotθBv=v0sinθCv=v0tanθDv=v0cosθ
Av=v0cotθBv=v0sinθCv=v0tanθDv=v0cosθTwo equal negative charges are fixed at points and on y-axis. A positive charge Q is released from rest at the point on the x-axis. The charge Q will:
Aexecute simple harmonic motion about the originBmove to the origin and remain at restCmove to infinityDsame as at point 25 cm aways form the surfaceA two point charges 4q and -q are fixed on the x - axis x=−d2andx=d2 , respectively. If a third point charge 'q' is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will
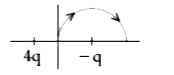 Aincrease by 2q23πε0dBdecrease by 4q23πε0dCincrease by 3q24πε0dDdecrease by q24πε0d
Aincrease by 2q23πε0dBdecrease by 4q23πε0dCincrease by 3q24πε0dDdecrease by q24πε0d
A thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?

View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
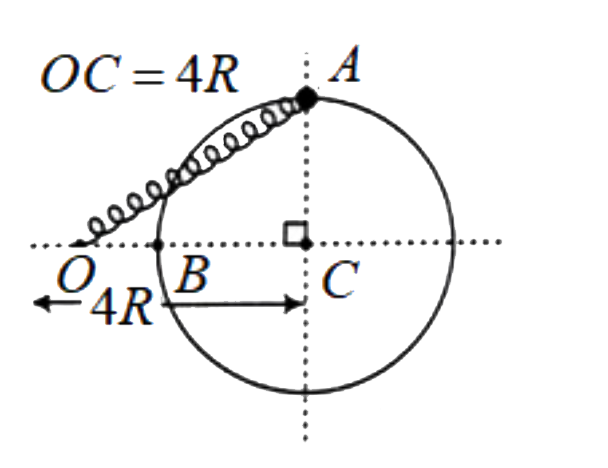
View SolutionTwo equal positive charges Q are fixed at points (a, 0) and (−a,0) on the x-axis. An opposite charge -q at rest is relased from point (0, a) on the y-axis. The charge -q will
View SolutionTwo point charges(+Q) and (−2Q) are fixed on the X-axis at position a and 2a from origin respectively. At what position on the axis, the resultant electric field is zero
View SolutionTwo point charges(+Q) and (−2Q) are fixed on the X-axis at position a and 2a from origin respectively. At what position on the axis, the resultant electric field is zero
View Solution

