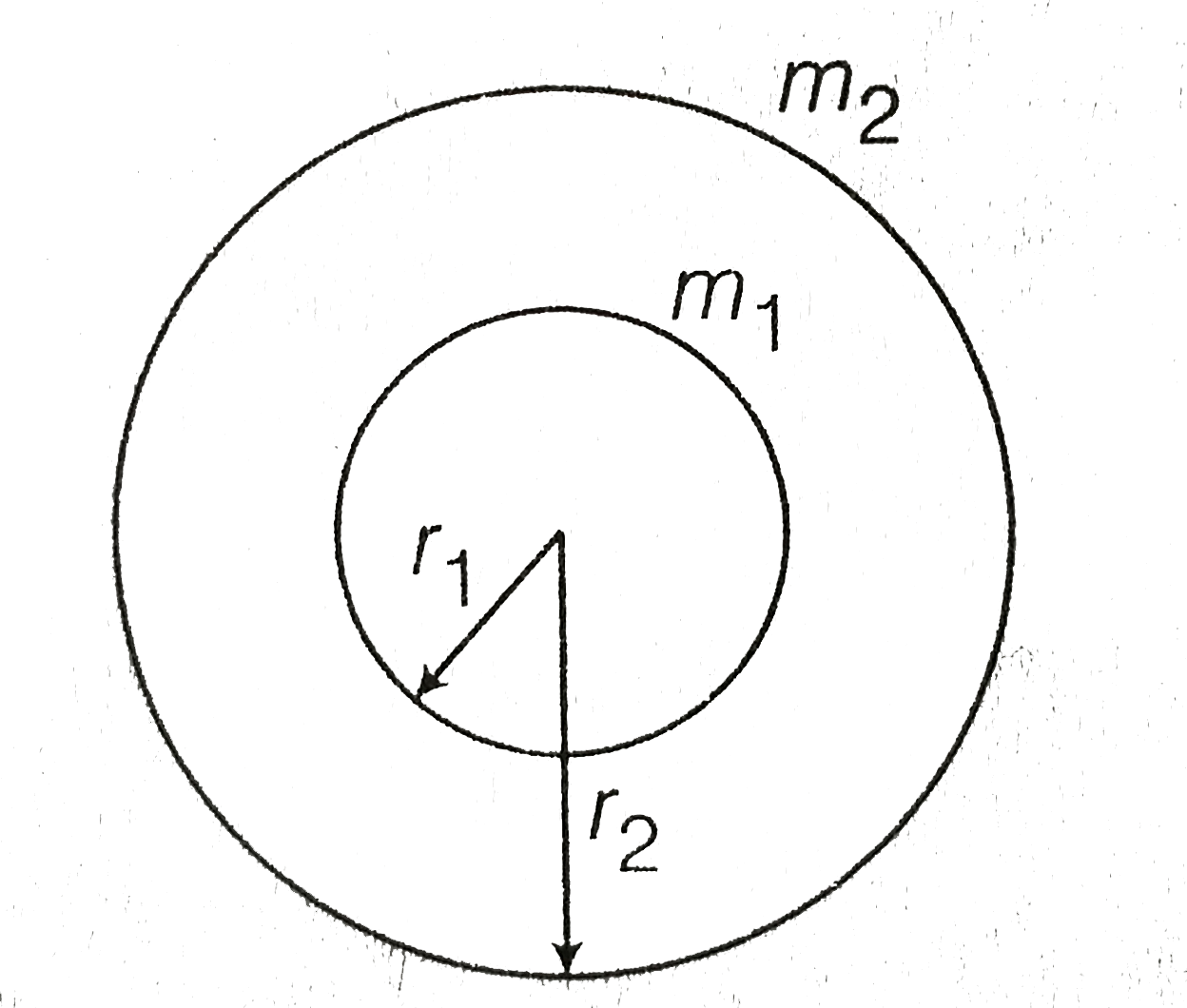
Two concentric shells of masses $M_{1}$ and $M_{2}$ are having radii $r_{1}$ and $r_{2}$ . Which of the following is the correct expression for the gravitational field on a mass $m$ ?

$F = \frac{G (M_{1} + M_{2})}{r^{2}}$ , for $r < r_{1}$

$F = \frac{G (M_{1} + M_{2})}{(r^{2})}$ , for $r < r_{2}$

$F = \frac{G M_{2}}{r^{2}}$ , for $r_{1} < r < r_{2}$

$F = G \frac{M_{1}}{r^{2}}$ , for $r_{1} < r < r_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Gravitational field inside a shell is zero, but for points outside it, the shell behaves as if whole of its mass is concentrated at its centre. Hence, for a point lying in between the shells there will be a field only due to the inner shell $(= G M_{2} / r^{2})$ because the point will be an external point for the inner shell but internal for the outer shell.

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

Assertion : Two spherical shells have masses $m_{1} and m_{2}$ . Their radii are $r_{1} and r_{2}$ . Let $r$ be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for $O < r < r_{1}$

Reason : In the region $r_{1} < r < r_{2}$ , gravitational field strength due to $m_{2}$ is zero. But gravitational potential due to $m_{2}$ is constant (but non-zero).
AIf both Assertin and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is false
DIf Assertion is false but Reason is true
Consider three concentric shells of masses $M_{1}, M_{2} and M_{3}$ having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P is
A $\frac{G (M_{1} + M_{2})}{y^{2}}, \frac{G (M_{1} + M_{2})}{y^{2}}$
B $\frac{G (M_{1} + M_{2} + M_{3})}{Y^{2}}, \frac{G (M_{1} + M_{2})}{x^{2}}$
C $\frac{G (M_{1} + M_{2} + M_{3})}{a^{2}}, \frac{G M_{1}}{a^{2}}$
D $\frac{G (M_{1} + M_{2} + M_{3})}{C^{2}}, \frac{G M_{2}}{b^{2}}$
Two concentric shells of different mass $m_{1}$ and $m_{2}$ are having a sliding particle of mass $m$ . The forces on the sliding at positions $I, I I$ and $I I I$ are respectively

A $0, \frac{G m_{1}}{r_{2}^{2}}, \frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}$
B $\frac{G m_{2}}{r_{2}^{2}}, 0, \frac{G m_{1}}{r_{1}^{2}}$
C $\frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}, \frac{G m_{2}}{r_{2}^{2}}, 0$
D $\frac{G (m_{1} + m_{2}) m}{r_{1}^{2}}, \frac{G (m_{2}) m}{r_{2}^{2}}, 0$

CENGAGE PHYSICS-GRAVITATION-Single Correct

Home
Ask Doubt
Profile

Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

Consider three concentric shells of masses M1,M2andM3 having radii a,b and c respectively are situated as shown in Gravitational field at a point located at Q and P is

Two concentric shells of different mass m1 and m2 are having a sliding particle of mass m. The forces on the sliding at positions I,II and III are respectively

CENGAGE PHYSICS-GRAVITATION-Single Correct

Two concentric shells of masses $M_{1}$ and $M_{2}$ are having radii $r_{1}$ and $r_{2}$ . Which of the following is the correct expression for the gravitational field on a mass $m$ ?

Consider three concentric shells of masses $M_{1}, M_{2} and M_{3}$ having radii a,b and c respectively are situated as shown in

Gravitational field at a point located at Q and P is

Two concentric shells of different mass $m_{1}$ and $m_{2}$ are having a sliding particle of mass $m$ . The forces on the sliding at positions $I, I I$ and $I I I$ are respectively