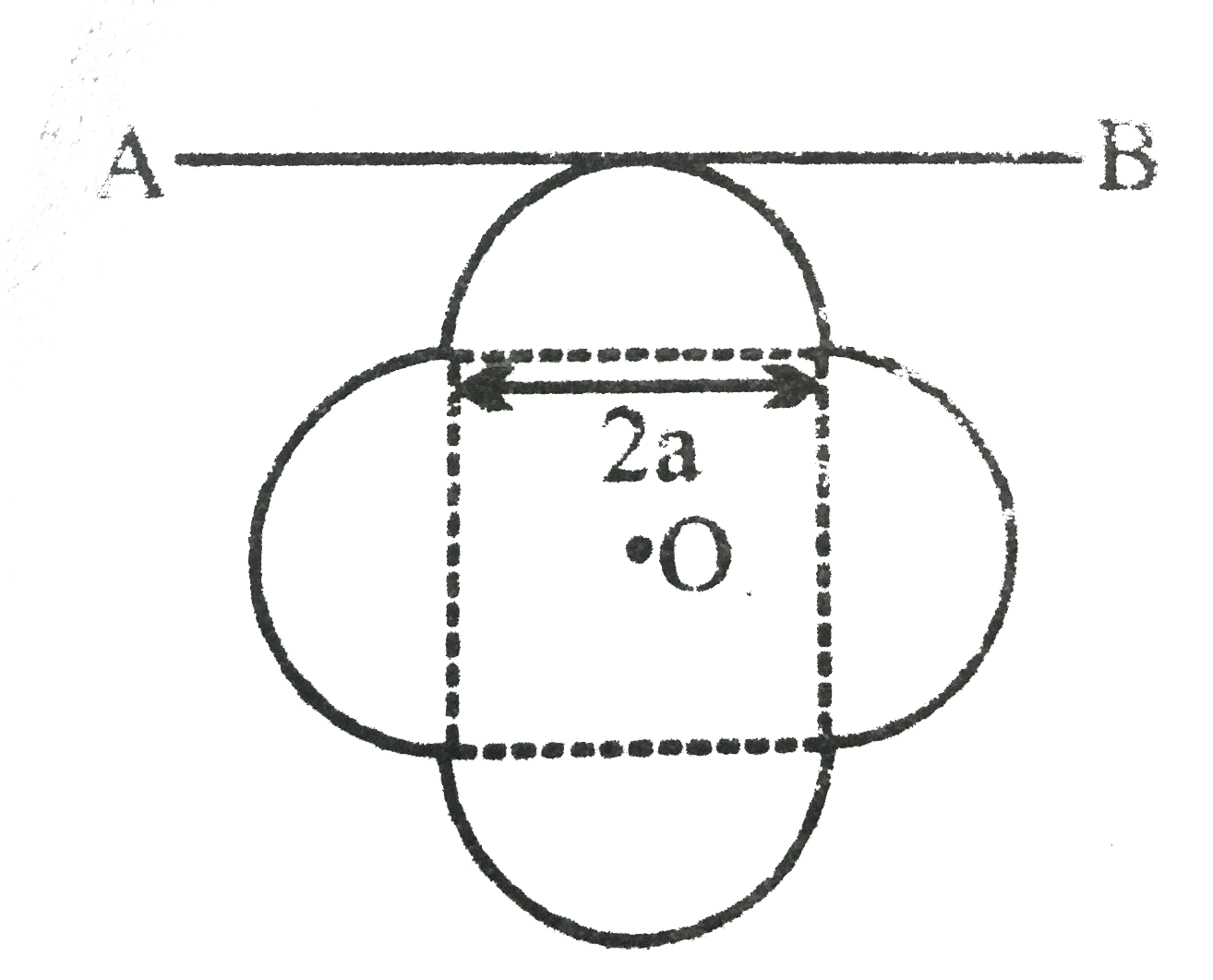
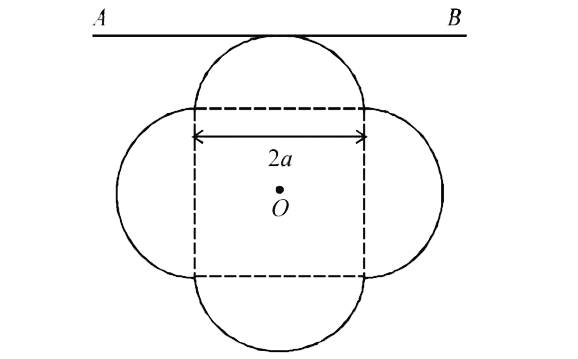
A symmetric lamina of mass $M$ consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is $2 a$ .
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is $1.6 M a^{2}$ . The moment of inertia of the lamina about the tangent $A B$ in the plane of lamina is.
.

Video Solution

Text Solution

Verified by Experts

Assuming symmetric lamina to be in $x y$ plane we will have

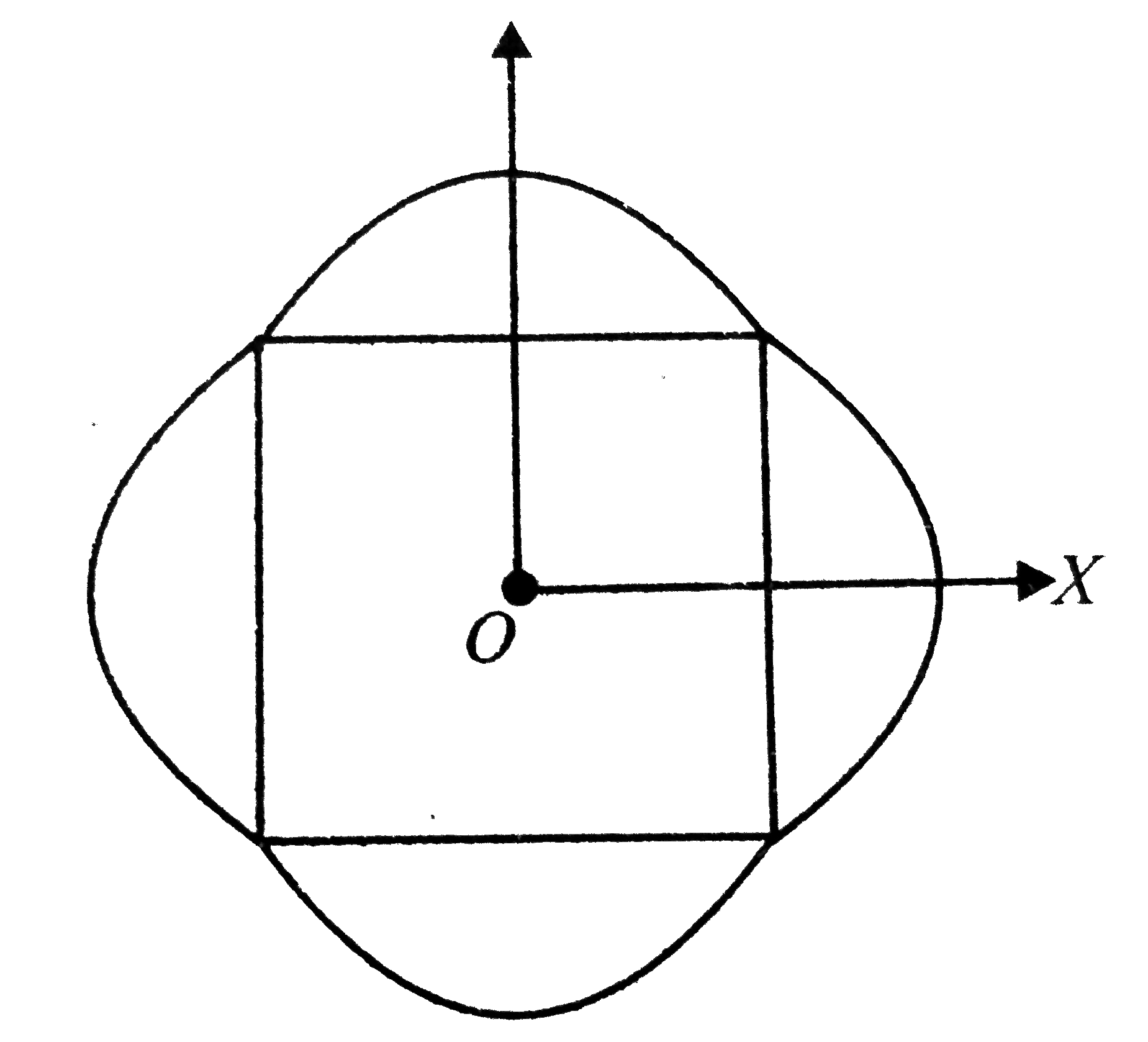
$I_{x} = I_{y}$ (since the mass distribution is the mass about the $x$ -axis and $y$ -axis)
$I_{x} = I_{y} = I_{z}$ (perpendiclar axis theorem)
it is given that
$I_{z} = 1.6 M a^{2}$
Hence $I_{x} = I_{y} = \frac{I_{z}}{2} = 0.8 M a^{2}$
Now according to the paralel axis theorem, we get
$I_{A B} = I_{X T} M {(2 a)}^{2}$
$= 0.8 M a^{2} + 4 M a^{2} = 4.8 M a^{2}$

Updated on:21/07/2023

The moment of inertia of a circular disc about an axis passing through its centre and perpendicular to the plane is $4 k g m^{2}$ . Its moment of inertia about the diameter is
A $2 k g m^{2}$
B $6 k g m^{2}$
C $4 k g m^{2}$
D $8 k g m^{2}$
The moment of inertia of a disc an axis passing through its centre and perpendicular to its plane is I kg $m^{2}$ . Its moment of inertia about an axis coincident with the tangent to it is
AI
B $\frac{5}{4} I$
C $\frac{5}{2} I$
D $3 I$
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$