A ball (solid sphere) is thrown down the valley in such a way that it slides with a speed v0 initially without rolling. Prove that it will roll without any sliding when its speed falls to (57)v0. The transition from pure sliding to pure rolling is gradual, so that both sliding and rolling take place during this interval.
Method 1: Force/Torque Method: The forces acting on the ball are as shown in Fig. Let the acceleration of the centre of mass be aCM and its angular acceleration about the centre of mass axis be α as shown in the figure.

The following filgus represent the forces, accelerations and velocities of the ball in three different positions.
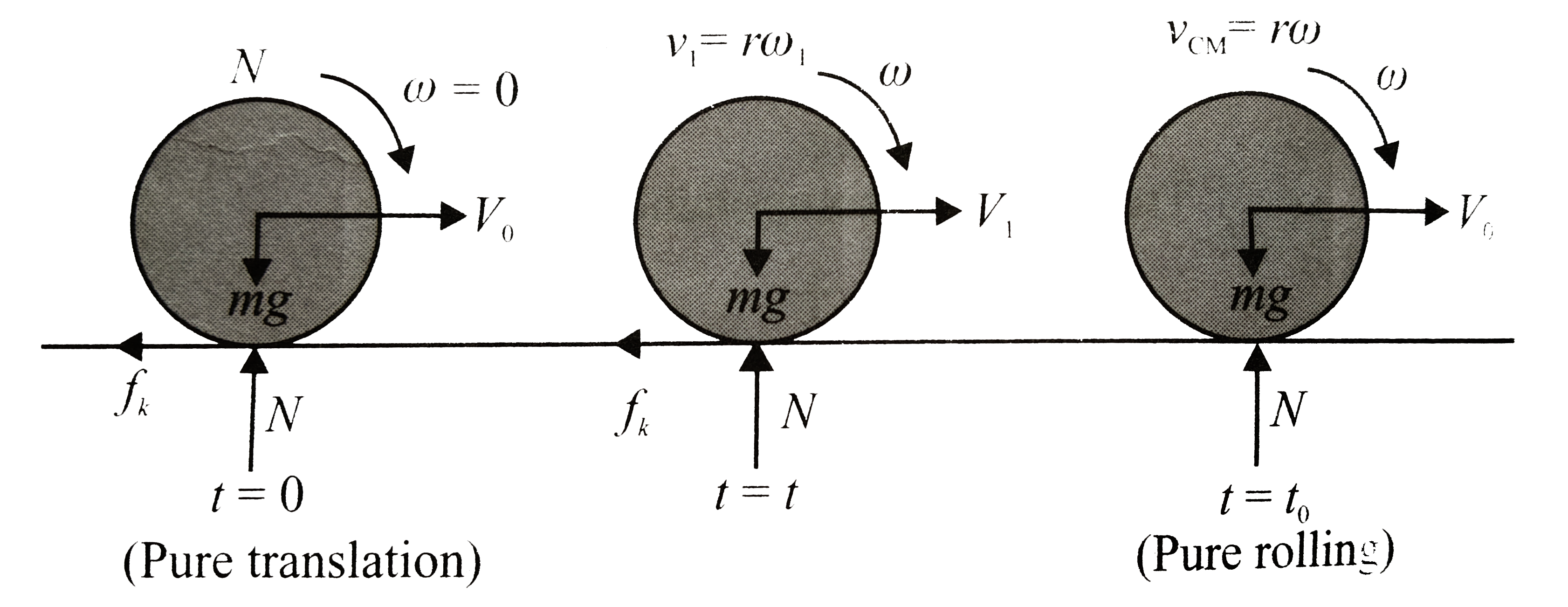
Force equations: N−mg=0(in the vertical direction)
−fk=maCM ( in the horizontal direction)
⇒aCM=−fkm...........i
And from τCM=ICMα
⇒fkr(25mr2)α
⇒α⎛⎝fkr25mr2⎞⎠..........ii
Let the velocity of the centre of mass be vCM and angular velocity about the centre of mass axis be ω when rolling starts.
vCM+v0+(−fkm)t (using v=u+at)...........iii
and ω=0+⎛⎝fkr25mr2⎞⎠t(ω=ω0+at)............iv
also vCM=rω
Solving eqn iii, iv, and v for vCM, we get
vCM=57v0
Method 2: Work Energy Theorem
Apply the work energy theorem for the translation and rotational components of the motion separately.
∑Wforce=△Ktranslational
∑Wtorque=△Krotational
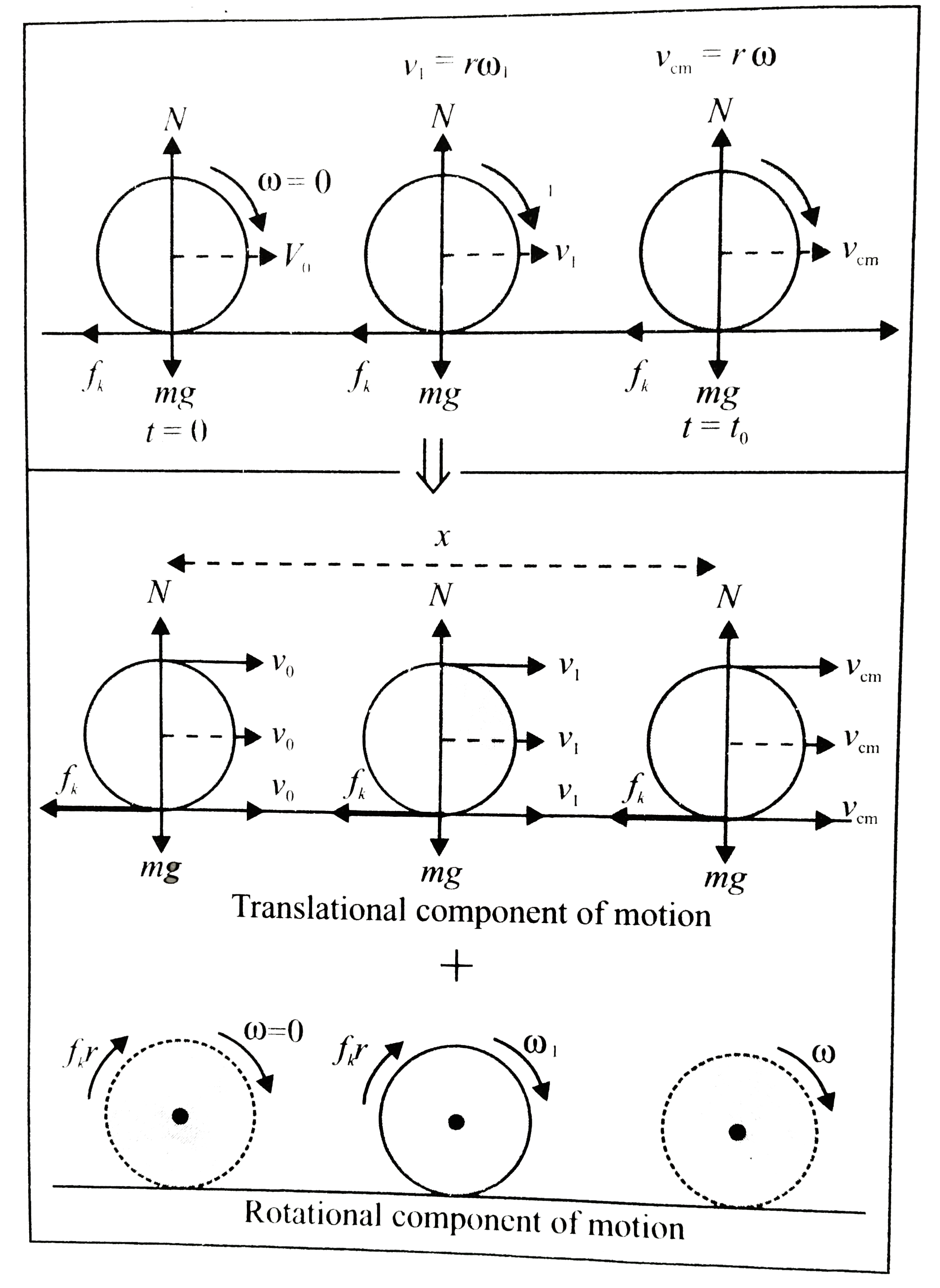
Mathematically Wfk+WN+Wmg=(K2−K2)translational
⇒−fkx+0+0=12mv2−12mv20
=−fk(vavt)=12(v2−v20)[∵x=vavt]
⇒−fk(v+v02)t=12m(v−v0)(v+v0) ............i
in case of constant acceleration only v−(av)=vi+vf2
And for the rotational component of motion
fkrθ=12ICMω2−0
→fkr(ωavt)=12ICMω2
⇒fkr(0+ω2)t=12×25mr2×ω2
[In case of constant angular acceleration ωav=ωi+ωf2]
⇒fkrω2t=12×25mr2ω2 ..............ii
From eqn i and ii we get
−fk(v+v0)2tfkrω2t=12m(v+v0)(v−v0)12×25mr2ω2
⇒1=v−v025ωr
But rω=v,
−1=v−v025ωr
⇒−25v=v−v0
⇒v0=v+25v=75v
⇒v=57v0
Method 3: By conservation of Angular Moentum
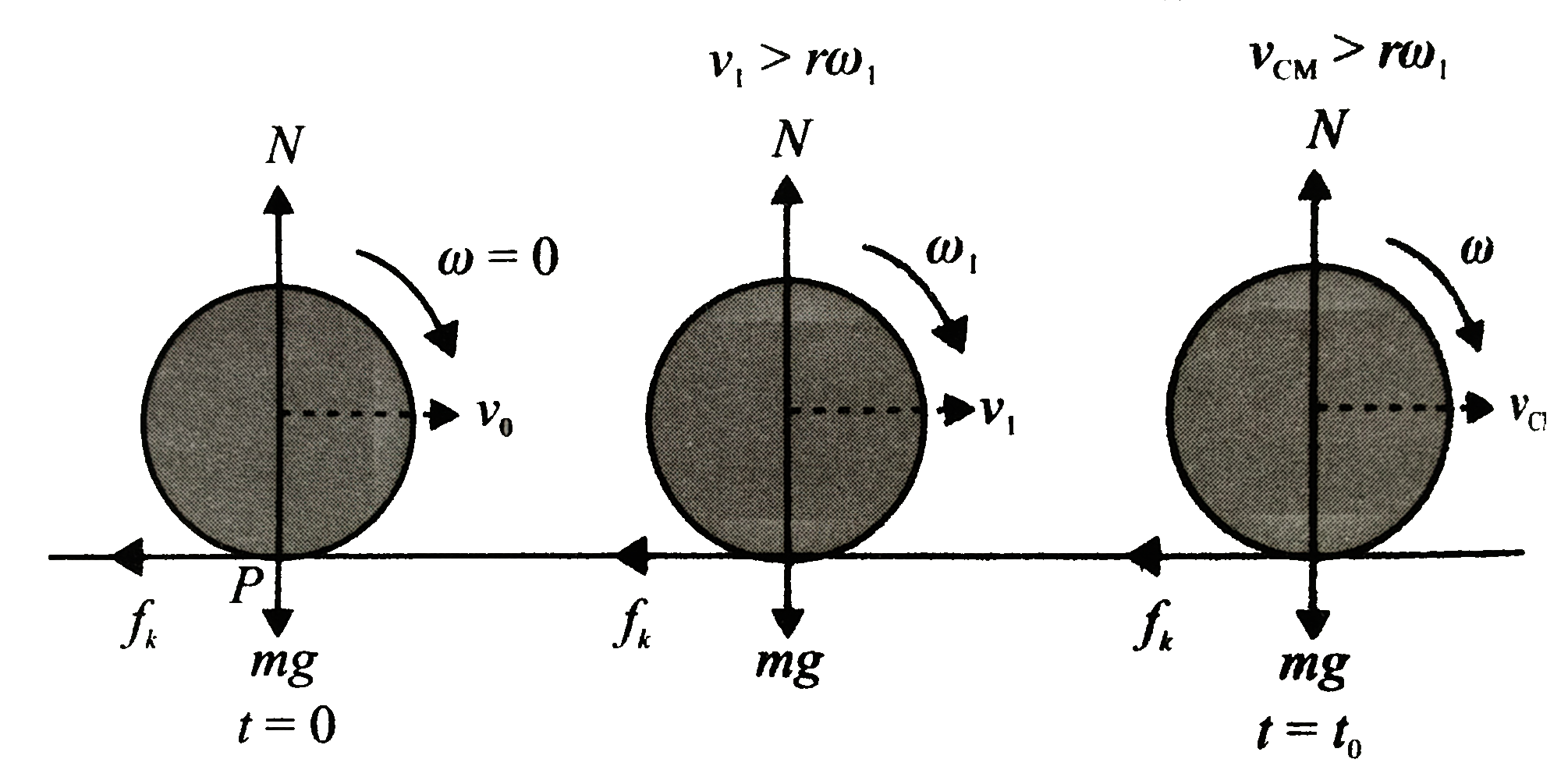
If →τ=0→dLdt=0,L= constant
The torque acting on the ball for all its position, about point P (a point on the ground as shown in figure. is zero. So the anguar momentum of the ball about poitn P will remain constant.
⇒mv0r=ICMω+mvr
⇒mv0r=25mr2(vr)+mvr(ω=vr)
⇒v0=25v+v
⇒v=57v0
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A ball is thrown down a lawn in such a way that it initially slides with a speed v0 without rolling. It gradually picks up rotational motion. Prove that it will be without sliding, that is, its motion will be pure rolling when its speed falls to 57v0.
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View Solution
Knowledge Check
A heavy disc is thrown on a horizontal surface in such a way that it slides with a speed V0 intially without rollind . It will start rolling without slipping when its speed is reduced
A13V0B23V0C35V0D57V0A ball is thrown down a lawn in such a way that it initially slides with a speed v0 without rolling. It gradually picks up rotational motion. Find the speed of the ball at which there will be rolling without slipping :
A27v0B25v0C57v0D35v0A heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
A3u5B2u5C5u7D2u7
A solid spherical ball is rolling without slipping towards a fixed inclined plane with speed V0. Find the maximum height, that the ball reached on the incline.
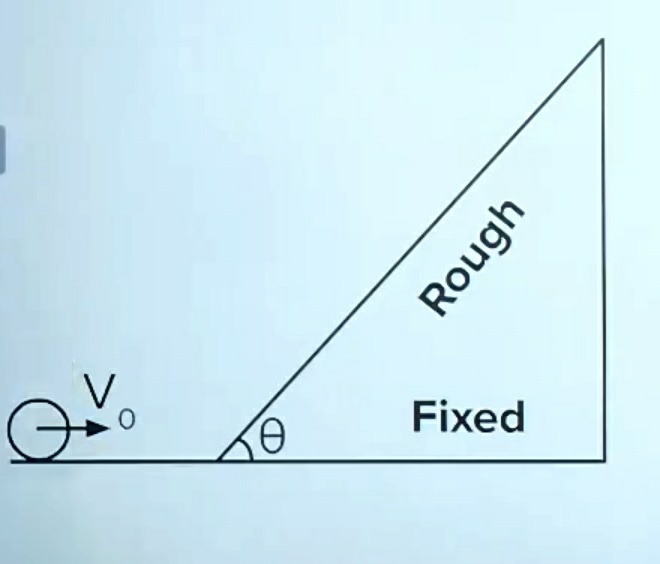
View SolutionA uniform disc of mass m and radius R is thrown on horizontal law in such a way that it initially slides with speed V0 without rolling. The distance travelled by the disc till it starts pure rolling is (Coefficient friction between the contact is 0.5)
View SolutionWhere must the cue hit a billiard ball so that it rolls without sliding form the start if R is the radius of the ball?
View SolutionOnly under gravity and some initial impulsea sphere cannot roll without sliding on :
View SolutionA thin hollow cylinder open at both ends
(i) Slides without rotating
(ii) Rolls without slipping, with the same speed.
The ratio of kinetic energies in the two cases is
View Solution
