A block of mass $m$ rests on a rough floor . The coefficient of friction between the block and the floor is $μ$
a. Two boys apply force $P$ at an angle $θ$ to the horizontal. One of them pushes the block , the other one pulls. Which one would reqire less efferts to cause impending motion of the block?
b. What is the minimum force required to move the block by pulling it ?
c. Shown that the block is pushes at a certain angle $θ_{0}$ it cannot be moved fro whatever the value of $P$ be

Video Solution

Text Solution

Verified by Experts

a.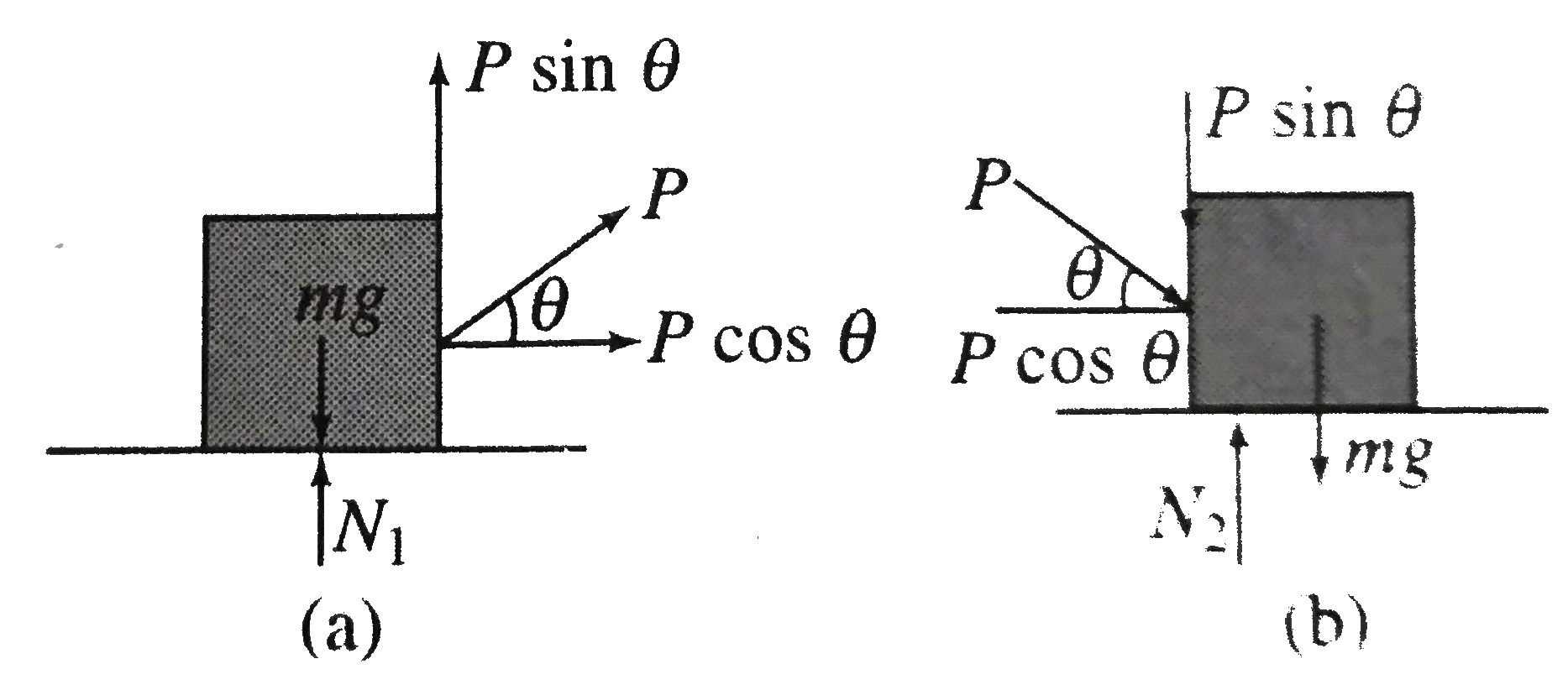
In first case $N_{1} = m g - p sin θ$
In second case $N_{2} = m g + p sin θ$
Since normal force in second case is greater so the friction will be greater in second case when the block impends the motion Hence in first case , less effort is required
b. $P cos θ = μ N_{1} = μ (m g - P sin θ) \to$ for first case
$\Rightarrow P = \frac{μ m g}{cos θ + μ sin θ} \Rightarrow p_{min} = \frac{μ m g}{\sqrt{1 + μ^{2}}}$
c. For pushing . $p cos θ > μ N_{2}$
$\Rightarrow p cos θ > μ (m g + p sin θ)$
$\Rightarrow p > \frac{μ m g}{cos θ - μ sin θ}$
As $θ$ increased $cos θ μ sin θ$ decreases and hence $P$ increase. Let as $θ = θ_{0}$ denominator because zero so
${cos θ}_{0} - μ - {sin θ}_{0} = 0 \Rightarrow θ_{0} = {cot}^{- 1} (μ)$
At $θ = θ_{0}, P > \infty$ which is not possible .

Updated on:21/07/2023

A block of mass m is placed on a rough floor of a lift . The coefficient of friction between the block and the floor is $μ$ . When the lift falls freely, the block is pulled horizontally on the floor. What is the force of friction -
A $μ m g$
B $μ m g / 2$
C $2 μ m g$
DNone of these
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , $g = 10 m / s^{2}$ )
A8.8N
B5.8N
C2.8N
D10.8N
In Fig. 7.149 , coefficient of friction between the block and the floor is $μ$ . Force F that will move the block on the floor with a uniform speed is :

A $(μ sin θ + cos θ) m g$
B $(μ sin θ - cos θ)$ mg
C $\frac{μ mg}{cos θ - μ sin θ}$
D $\frac{μ m g}{sin θ - μ cos θ}$