A metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
Take a small part of the ring which subtends an angle Δθ at the conter of the ring .Let T be the tension in the ring . The force act on the this part in the small part of ring Δm=m2πΔθ
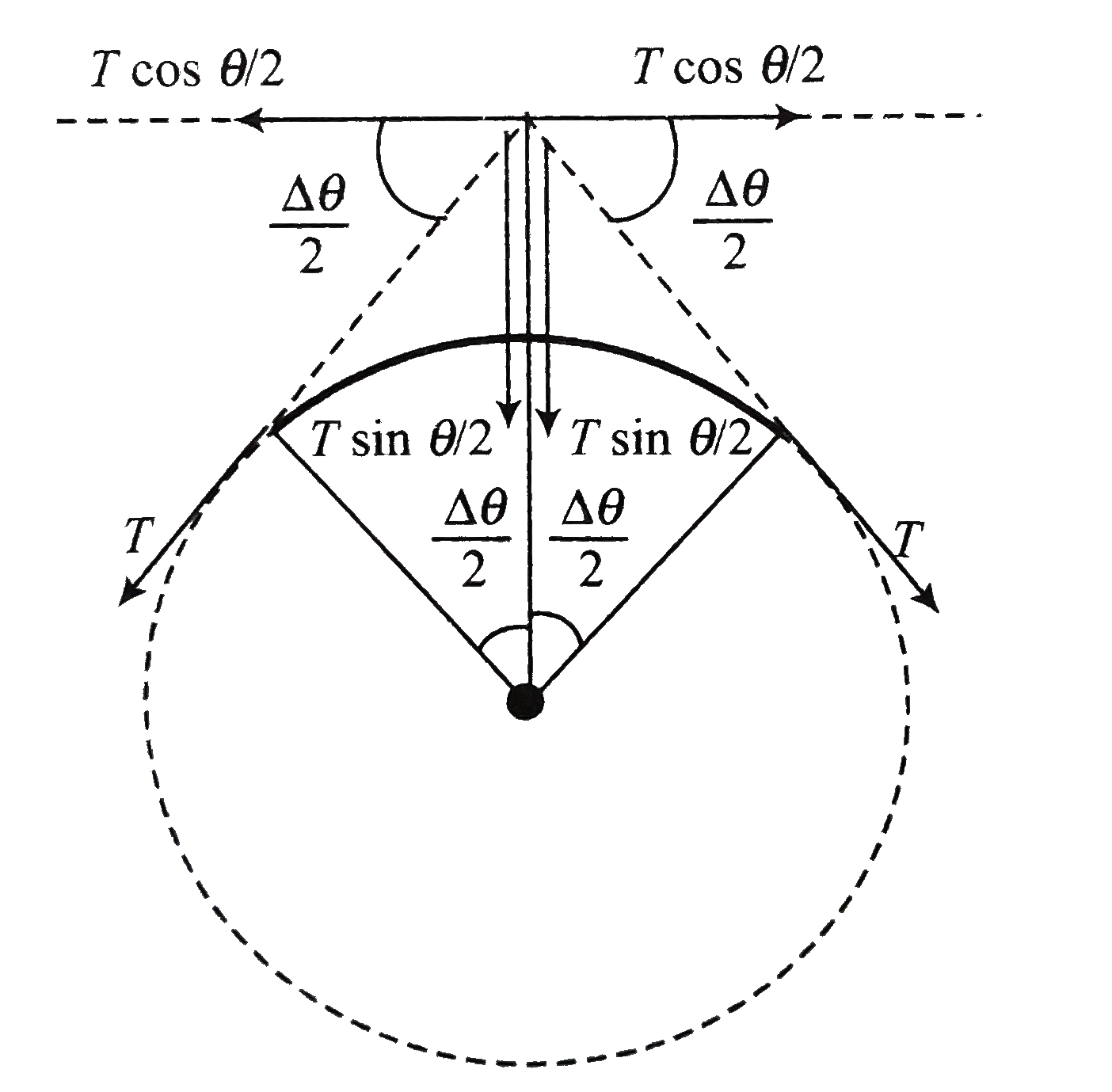
Thus, by Newton 's second law we have
2Tsin(Δθ)2=Δmv2R
As Δθ small, sin(Δθ)2=Δθ2
The above equation reduces in
2T(Δθ2)=(m2πΔθ)v2R
or T=mv22πR
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionA chain of mass m and radius R placed on a smooth table is revolving with a speed v about a vertical axis coinciding with the symmetry axis of the chain. Find the tension in the chain.
View Solution
Knowledge Check
A ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
AVRB2VRCV2RD√2VRA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 AvRB2vRCv2RD3vR
AvRB2vRCv2RD3vRFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,A912MR2B1112MR2C11.312MR2DMR2
,A912MR2B1112MR2C11.312MR2DMR2
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
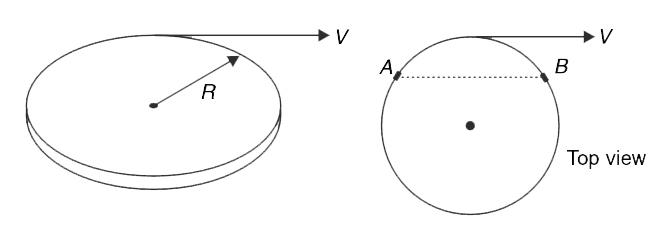
View SolutionA ring of mass M and radius R lies flat on a horizontal table. A light thread is wound around it and its free end is pulled with a constant velocity v.
(a) Two small segment A and B (see fig.) in the ring are rough and have a coefficient of friction μ with the table. Rest of the ring is smooth. Find the speed with which the ring moves.
(b) Find the speed of the ring if coefficient of friction is μ everywhere, for all points on the ring.
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionThere is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
View Solution
