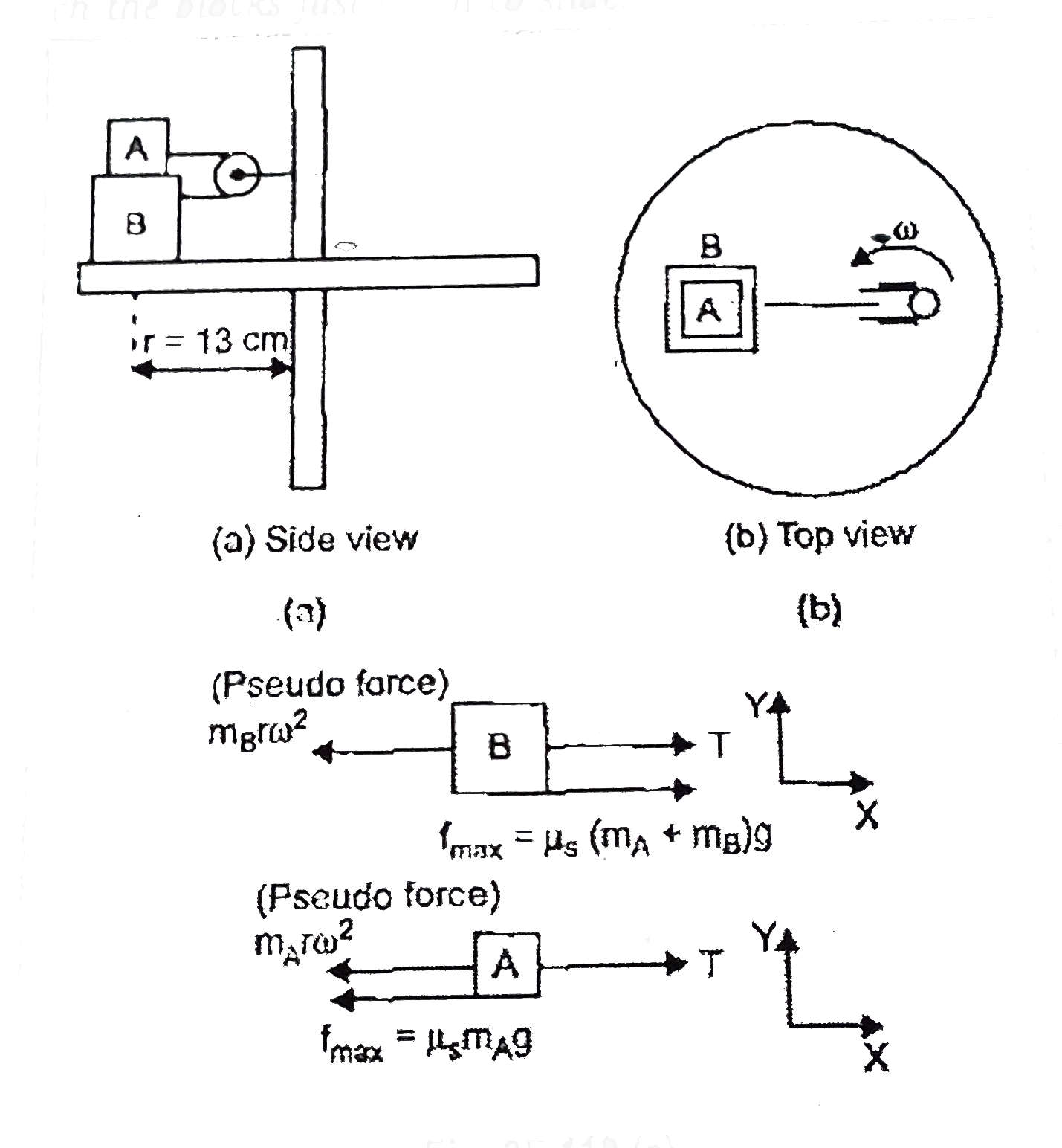
In fig two block of mass mAandmB are rotating at radius r kept on a rough table consider friction (μ) between all the contact surface pulley is frictionless determine the angular speed of the turn table for which the blocks just begin to slide

Equation for block B :
∑Fx=T+μsmA+mBg+μsmAg−mBrω2=0

Equation for block A :
∑Fx=T−μs(mA)g−(mArω2)=0 ...(i)
From equation (i) and (ii) , we climinate T as obtain
2μsmAg+μ(mA−mB)=(mB−mA)rω2
ω=[μsg(3mA+mB)r(mB−mA)]1/2
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
In Fig. shown two blocks are kept on a rough table, where mA=0.9kg,mB=1.7kg,r=13cm,μs=0.1. Consider friction between all the contact surface, pulley is frictionless. Determine the angular speed of the turn-rable for which the blocks just begin to slide
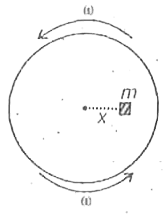
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
AThe maximum velocity of the block during the motion is PμmgBThe maximum velocity of the block during the motion is P2μmgCThe block's speed is never decreasing and finally becomes constantDThe speed of the block first increases to a maximum value and then decreasesA block m1, strikes a stationary blocks m3 inelastically. Another block m2, is kept on m3. Neglecting the friction between all contacting surfaces, the fractional decrease of KE of the system in collision is
Am1m1+m2+m3Bm1m2+m3Cm3m1+m3Dm2+m3m1+m2+m3
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

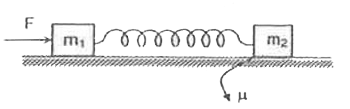
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View SolutionA block is kept on a horizontal table that is executing simple harmonic motion of frequency v in the horizontal plane. The coefficient of static friction between the block and the table is μ. Determine the maximum amplitude of the table for which the block does not slip on the surface of the table.
View SolutionTwo block of masses m and M are connected by a chord passing around a frictionless pulley which is attached to a rotating frame , which rotates about a vertical axis with an angular velocity ω If the coefficient of friction between the two masses and the surface are μ1 and μ2 respectively determine the value of ω at which the block starts sliding radially (M>m)

View SolutionA block m1 strikes a stationary block m3 inelastically. Another block m2 is kept on m3. Neglecting the friction between all contacting surfaces, calculate the fractional decrease in KE of the system in collision.
View Solution
