A block of mass m lying on a horizontal surface (coefficient of static friction =μs) is to be brought into motion by a pulling force F At what angle θ with the horizontal should the force F be applied so that its magnitude is minimum ? Also find the minimum magnitude

Let us first calculate the force F required to bring m into motion in terms of angle θ Equation using laws of motion are as follows:
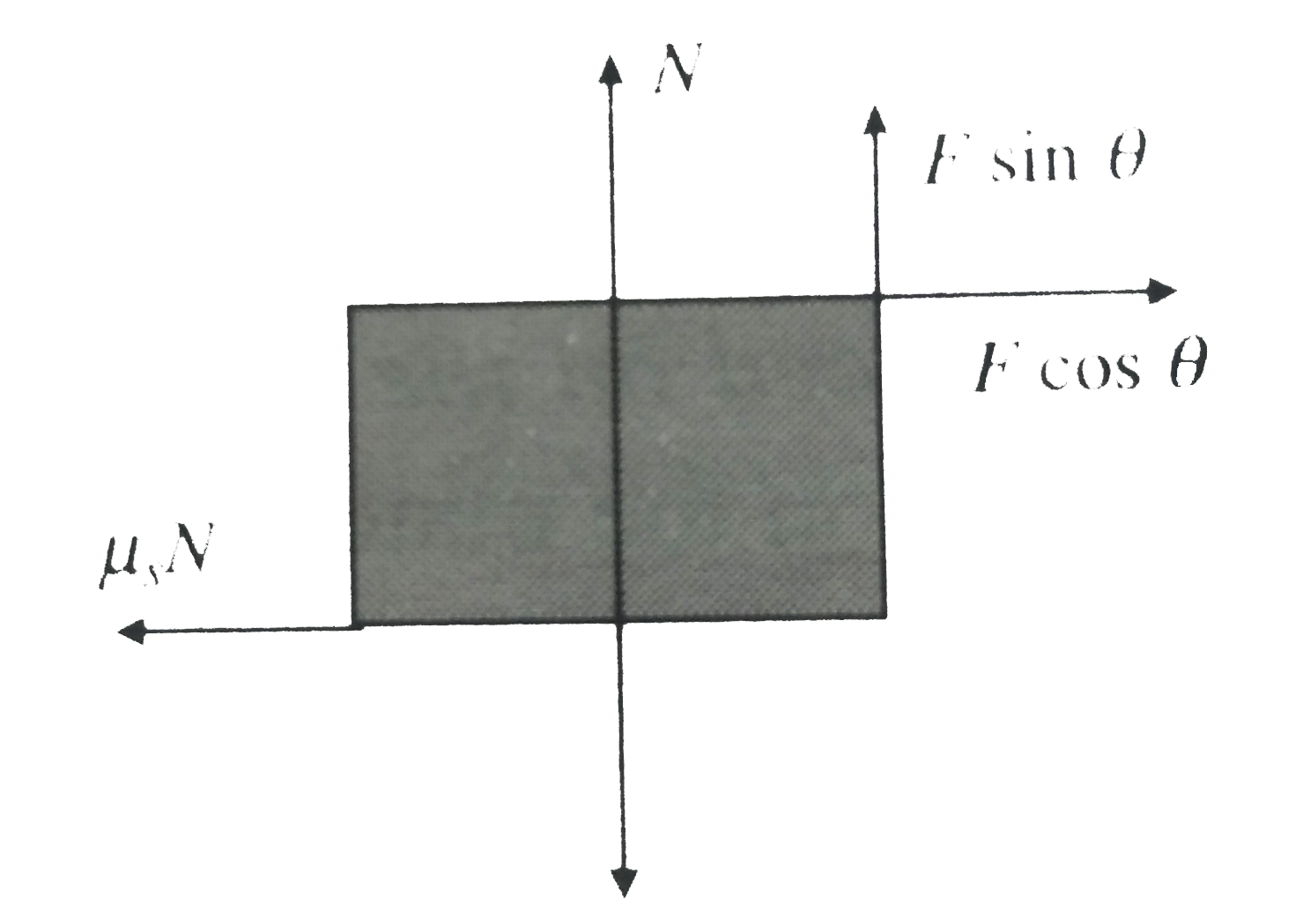
N=mg−Fsinθ
andFcosθ=μ0N
Fcosθ=μ,(mg−Fsinθ)
⇒F=μsmgcosθ+μssinθ
 We have to find the angle θ For which this force F is minimum substituting μs=tanθ (for simplification), we get
We have to find the angle θ For which this force F is minimum substituting μs=tanθ (for simplification), we get
F=mgtanϕcosθ+tanϕsinθ=mgsinϕcos(θ−ϕ)
F is minimum is cos(θ−ϕ)maximum ,Hence F is minimum for θ=ϕ=tan−1μs, and Fmin=mgsinθ
To bring m into motion with least effect force should be applied at an angular tan−1μs and should have a magnitude equal to
Fmin=mgsinϕ=μsmg√1+μ2s
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
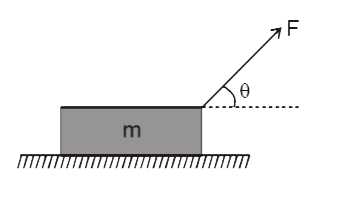
A wooden block of mass m resting on a rough horizontal table (coefficient of friction =μ ) is pulled by a force F as shown in figure.The acceleration of the block moving horizontally is:
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View Solution
Knowledge Check
A block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
Aμ=tanθBμ=cosθCμ=sinθDμ=cotθA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
A25NB5NC10NDZeroA block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
Amgsinϕcos(θ−ϕ)Bmgcosϕcos(θ−ϕ)CmgtanϕDmgsinϕ
A block of mass 1kg is at rest on a rough horizontal surface having coefficient of static friction 0.2 and kinetic friciton 0.15, find the frictional forces if a horizontal force,
(a) F=1N (b) F=1.96N (c) F=2.5N is applied on a block

View SolutionA block of mass m rests on a horizontal floor for which coefficient of friction is μ . Find the magnitude and the direction of force that should be applied to just move the block so that the applied force is minimum.
View SolutionA block of mass m is placed on a horizontal surface. The coefficient of frication between them is μ. The block has to be moved by applying a single external force on it. The force may be applied in my direciton. The minimum value of this force must be
View SolutionA block of mass m lying on a rough horizontal surface of friction coefficient μ is pulled by a force F as shown , the limiting friction between the block and surface will be
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and Kinetic friction are 0.3and0.1 and g=10m/s−2 If a horizontal force of 50N is applied on the block, the frictional force is
View Solution
