A smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R/4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant K=mg/R. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

1. The free-body diagram of the ring is shown in fig. the force acting on the ring are:
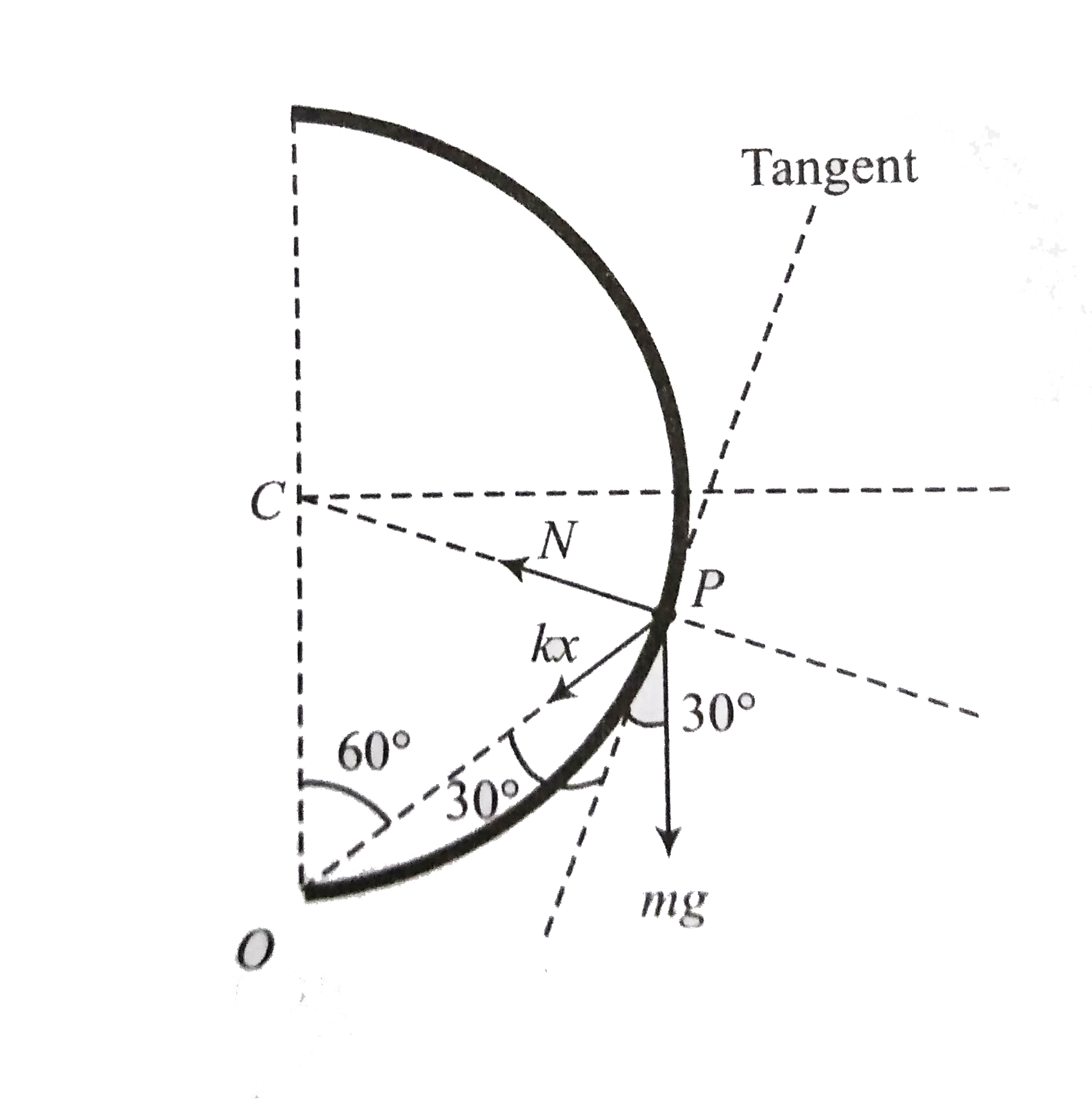
a. The weight mg acting vertically downwards
(b) Normal force N by the wire track.
Normal force on the ring could be either radially outwards or radially inwards depending on whether the ring presses against the inner surface or outer surface of the track. To ascertaion whether normal force is inwards or outwards, assume thatm to begin with, it is inwards. Then from Σ→F=m→a, find the value of normal force. If it is positive, it is inwards and if it id negative, it is outwards.
(c ) Force of the spring kx. In the given physical situation, the spring is extended, it will pull the ring. So the spring force kx is along the spring towards O.
2. Lenght of spring in the position shown=R.(CP=CO=R, ∠COP=∠OPC=60∘,∠COP is equilateral)
Change in length of the spring =R−(34)R=(R4)
kx=(mgR)(R4)=mg4
Now from Ft=mat,
(mg4)cos30∘+mgcos30∘=mat⇒at=5√38g
Now consider in radial direction
N+kxcos60∘=mgcos60∘
N=mgcos60∘−kxcos60∘
=mg(12)−(mg4)⋅(12)=38mg.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
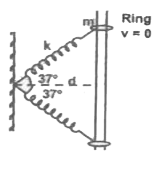
one end of a spring of naturla length ha and spring constant k is fixed at the ground and the other is fitted with a smooth ring of mass m which is alowed to slide on a horizontal rod fixed at a height h figure. Initialy, the spring makes an angle of 370 with the vertical when teh system is released from rest. find teh speed of the ring when teh spring becomes vertical.

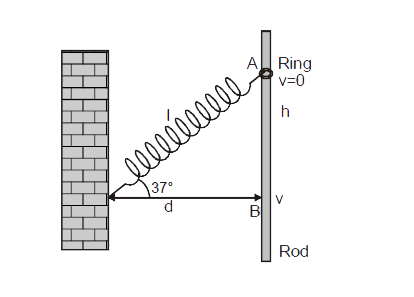
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
View Solution
Knowledge Check
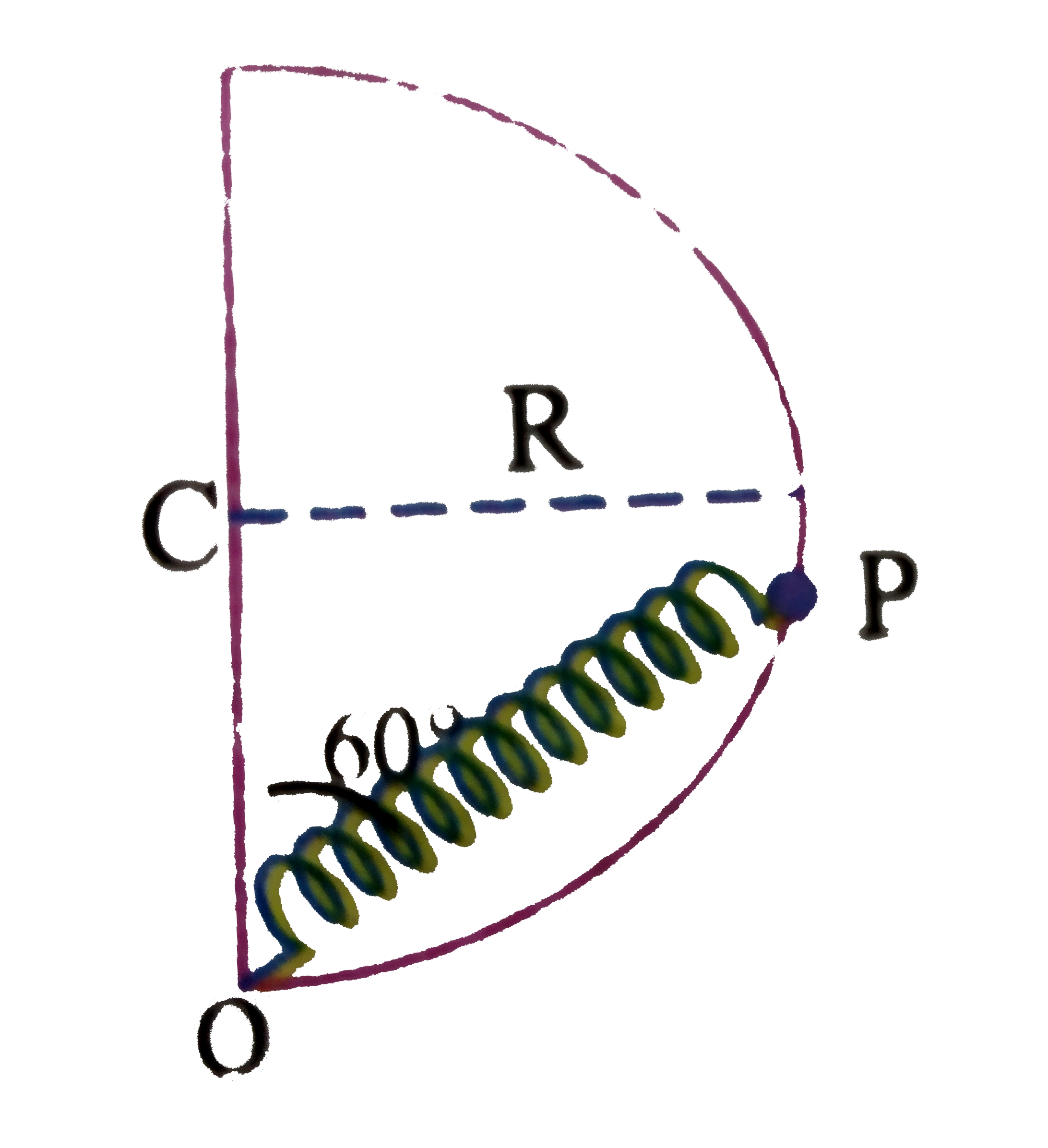
A smooth semicircular wire track of radius R if fixed in a vertical plane. One end of massless spring of netural length 3R4 is attached to the lowest point O of the wire track. A small ring of mass m which can slide on the track is attched to the other end of the spring. the ring is held stationary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant is K=mgR. considering the instance when the ring is released, the free body diagram of the ring, when aT is tengential acceleration, F is restoring force and N is normal reaction is
 A
A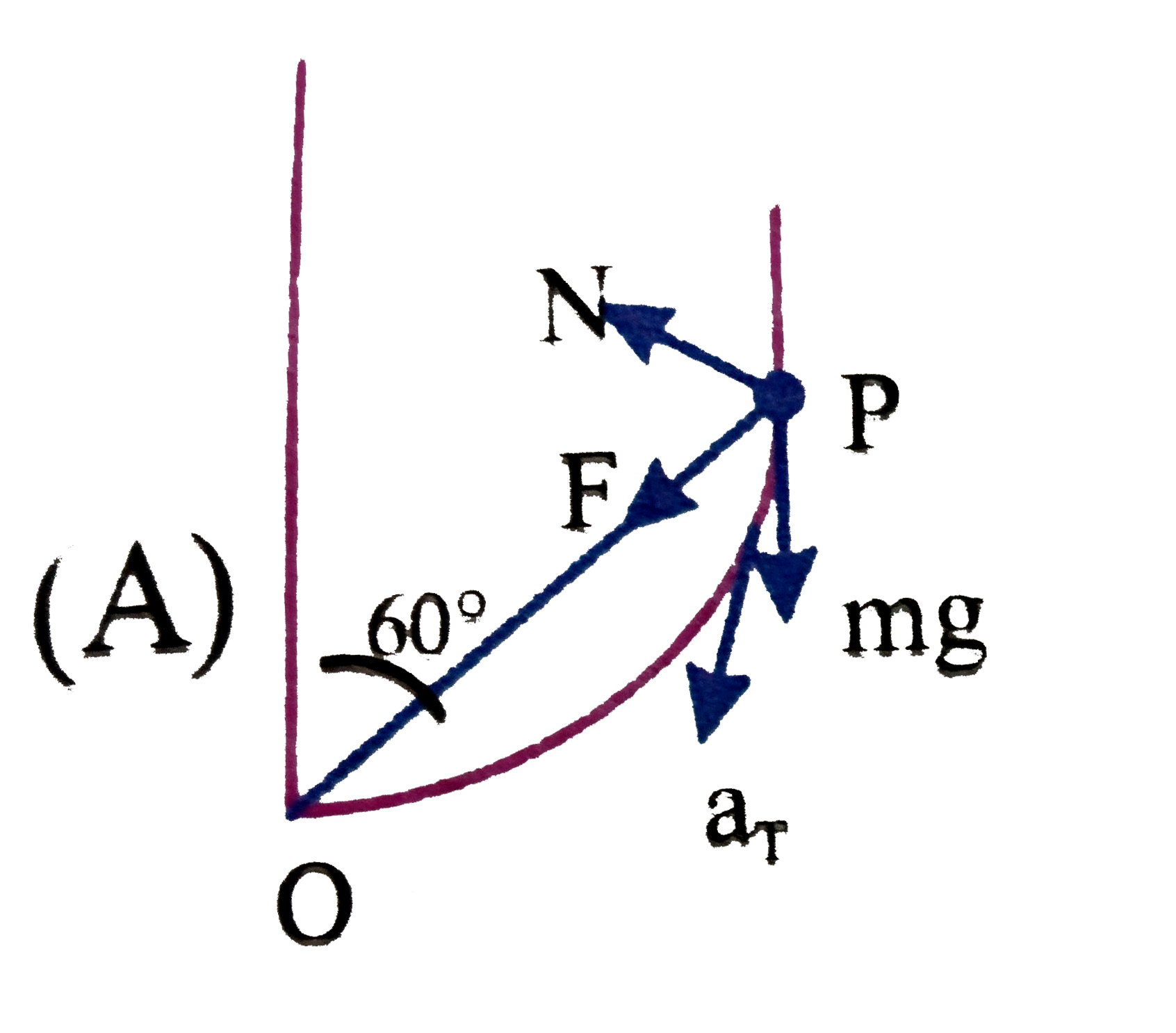 B
B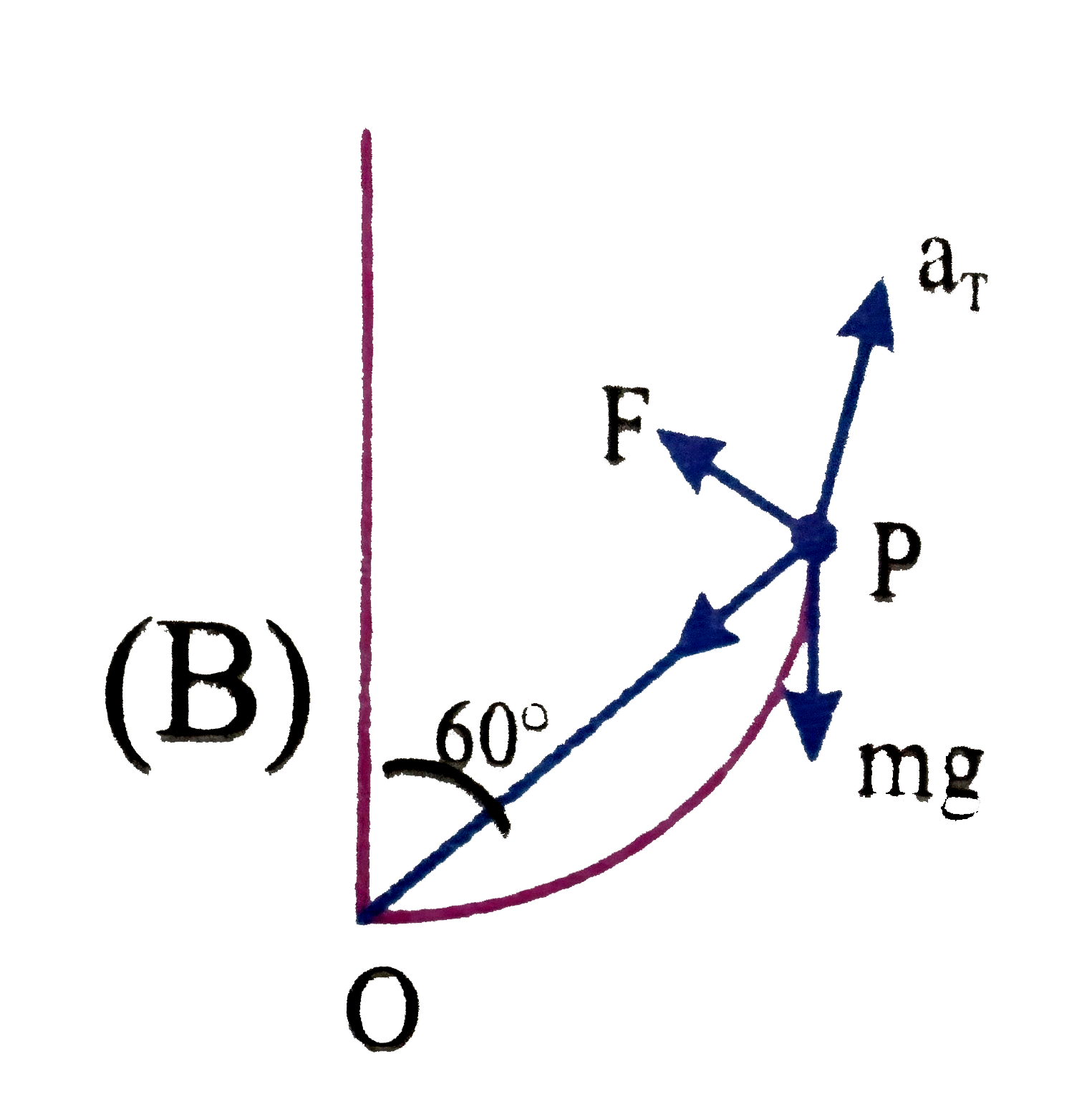 C
C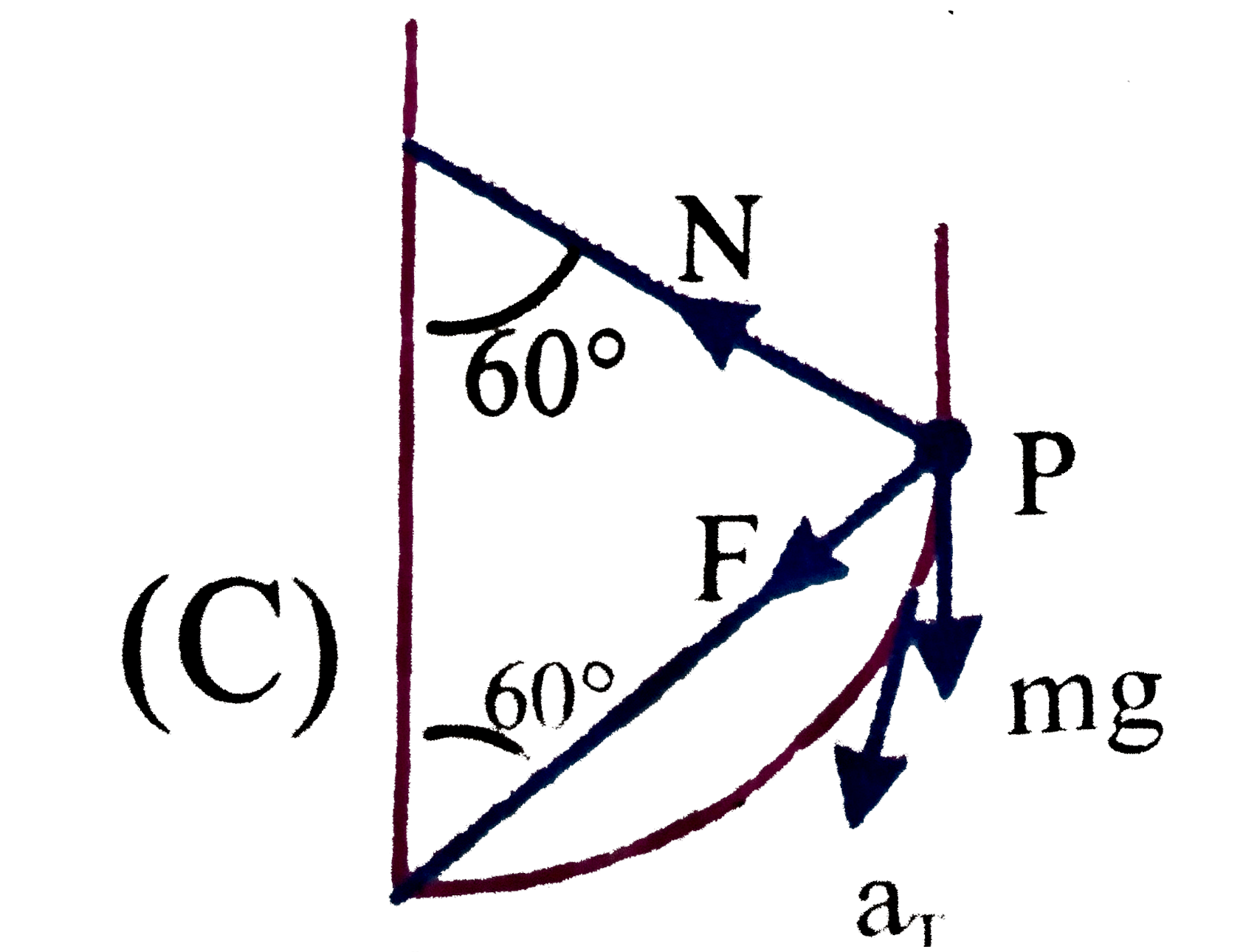 D
D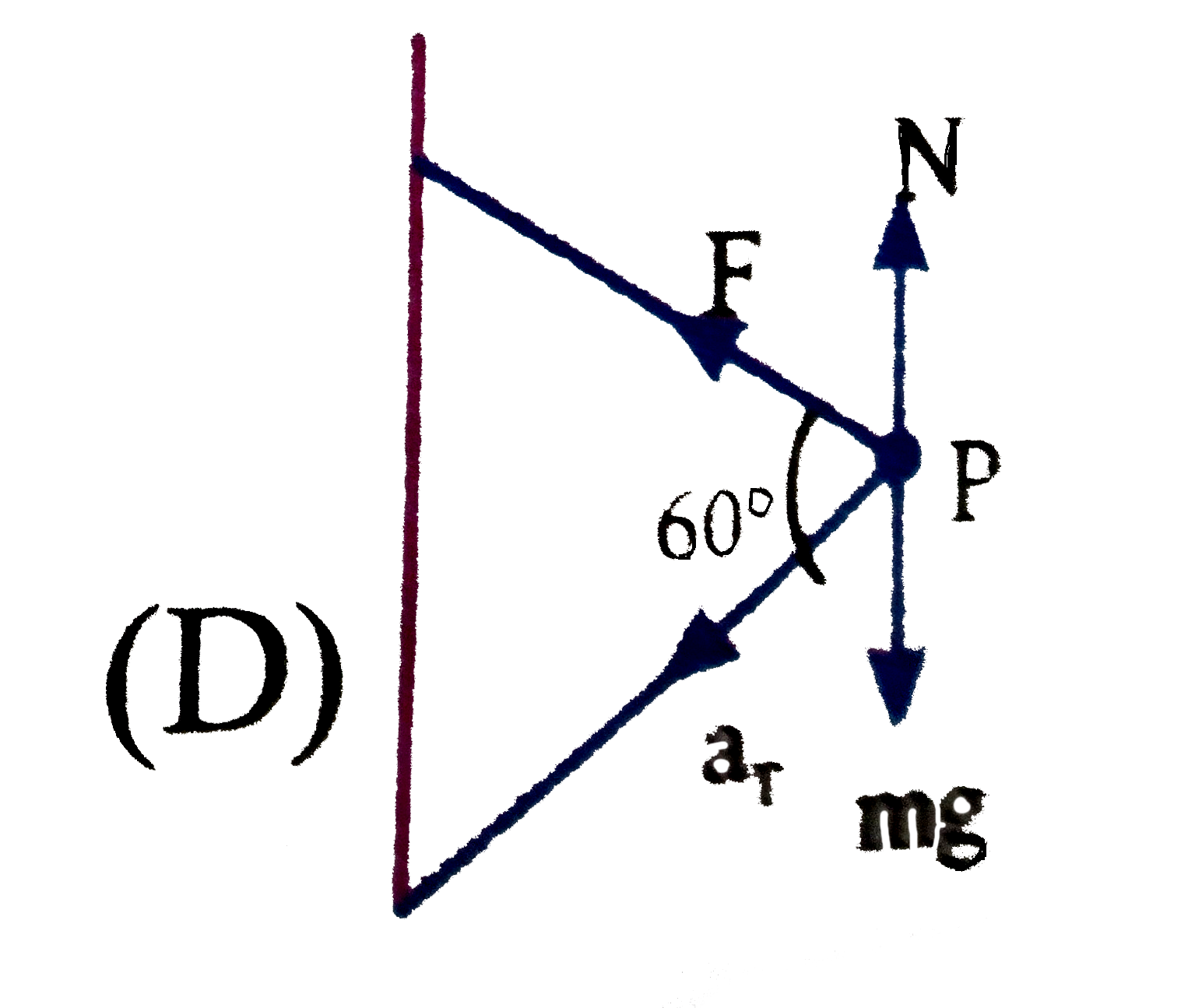
A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
Athe block will perform SHM of amplitude 5cmBthe block will have maximum velocity 30√5cm/sCthe block will have maximum acceleration 15m/s2Dthe minimum elastic potential energy of the spring will be zeroA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
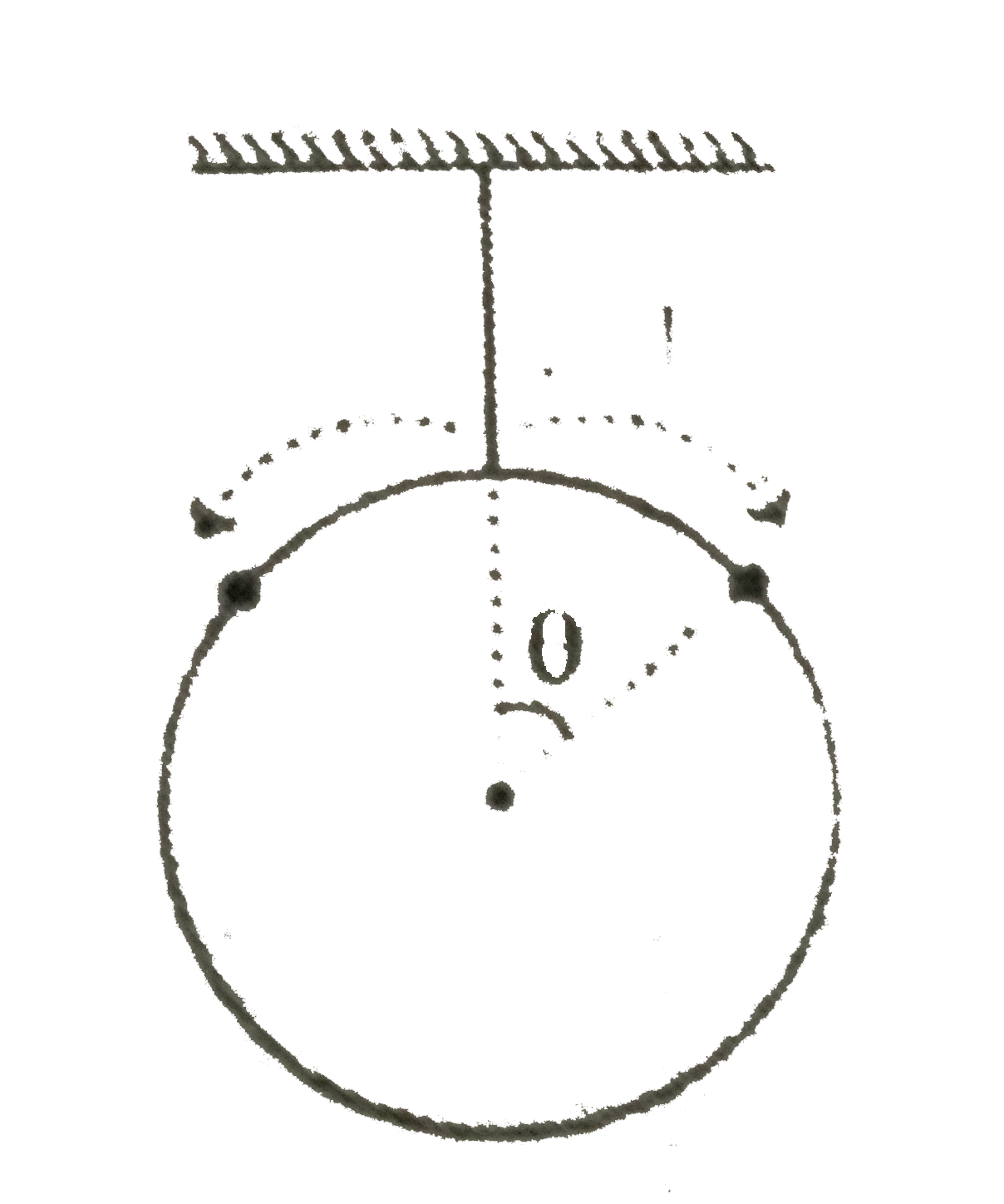 Aθ=sin−1[13(1+√1−GM3m)]Bθ=cos−1[53(1+√1−3M2m)]Cθ=cos−1[13(1+√1−3M2m)]Dθ=cos−1[13(1+√1−5M3m)]
Aθ=sin−1[13(1+√1−GM3m)]Bθ=cos−1[53(1+√1−3M2m)]Cθ=cos−1[13(1+√1−3M2m)]Dθ=cos−1[13(1+√1−5M3m)]
A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionOne end of a light spring of natural length 4m and spring constant 170 N/m is fixed on a rigid wall and the other is fixed to a smooth ring of mass 12 kg which can slide without friction in a verical rod fixed at a distance 4 m from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
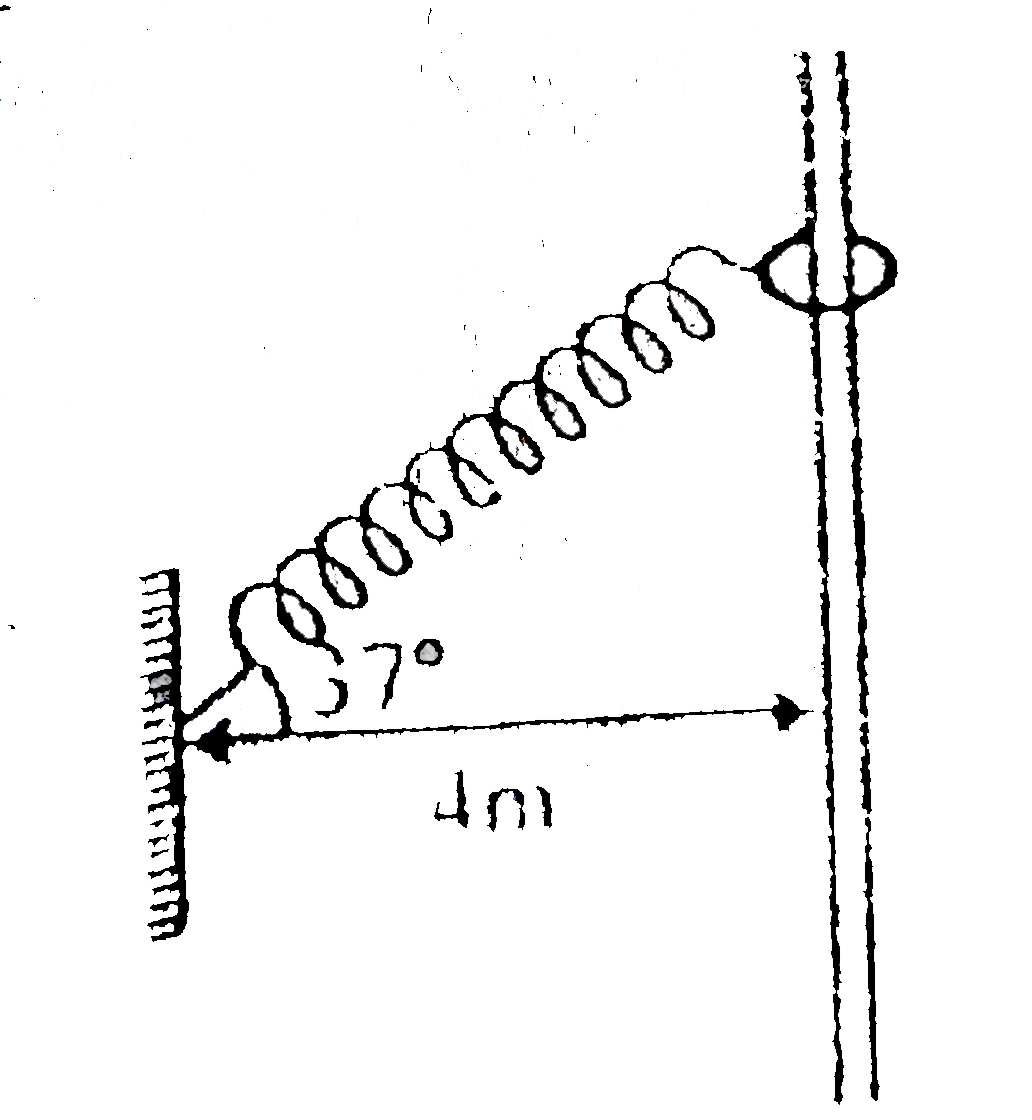
View SolutionOne end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
View SolutionA spring with one end attached to a mass and the other to a right support is stretched and released
View SolutionIn the figure shown there is a smooth tube of radius 'R' fixed in the vertical plane A ball 'B' of mass 'm'is released from the top of the tube B slides down due to gravity and compresses the spring the end 'C' of the spring is fixed and the end A is free Initially the line OA makes an angle of 60∘ with OC and finally it makes an angle of 30∘ after compression find the spring constant of the spring

View Solution
