A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
Method 1: Observation from ground frame. Let (ar) be the acceleration of the bead relative to the rod. Then arcosα is the leftward acceleration of the bead relative to the bead relative to the rod and arsinα is downward relative acceleration of the rod. If ay and ax be the absolute leftward horizontal and downward vertical acceleration of the bead , then
(→abead)x=(→abead,rod)x+(→arod)x
or ax=arcosα+a ...(i)
and arsinα=ay−0
or ay=arsinα...(ii)
From FBD of the bead (projecting forces vertically and horizontally)
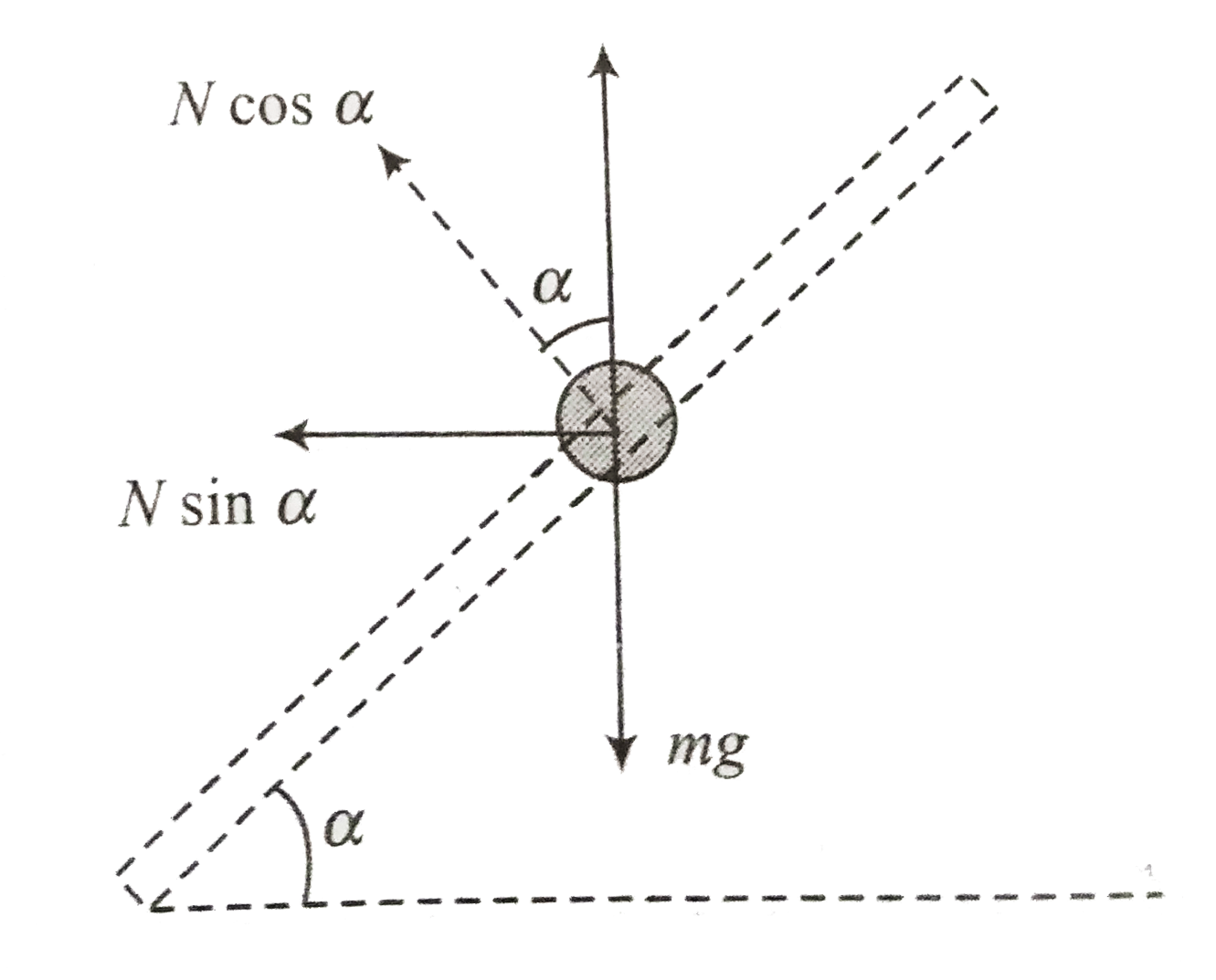
mg−Ncosα=marsinα ...(i)
and Nsinα=m(arcosα+a) ...(ii)
Eliminating N between (i) and (ii)
mgsinα=mar+macos(α)
or, ar=gsinα−asinα
Method 2: Observation from an observer moving with rod. Consider bead w.r.t rod i.e. from non-inertial frame. A pseudo force of magnitude ma will act on the bead in the direction opposite to accelerator of rod, i.e. in right direction
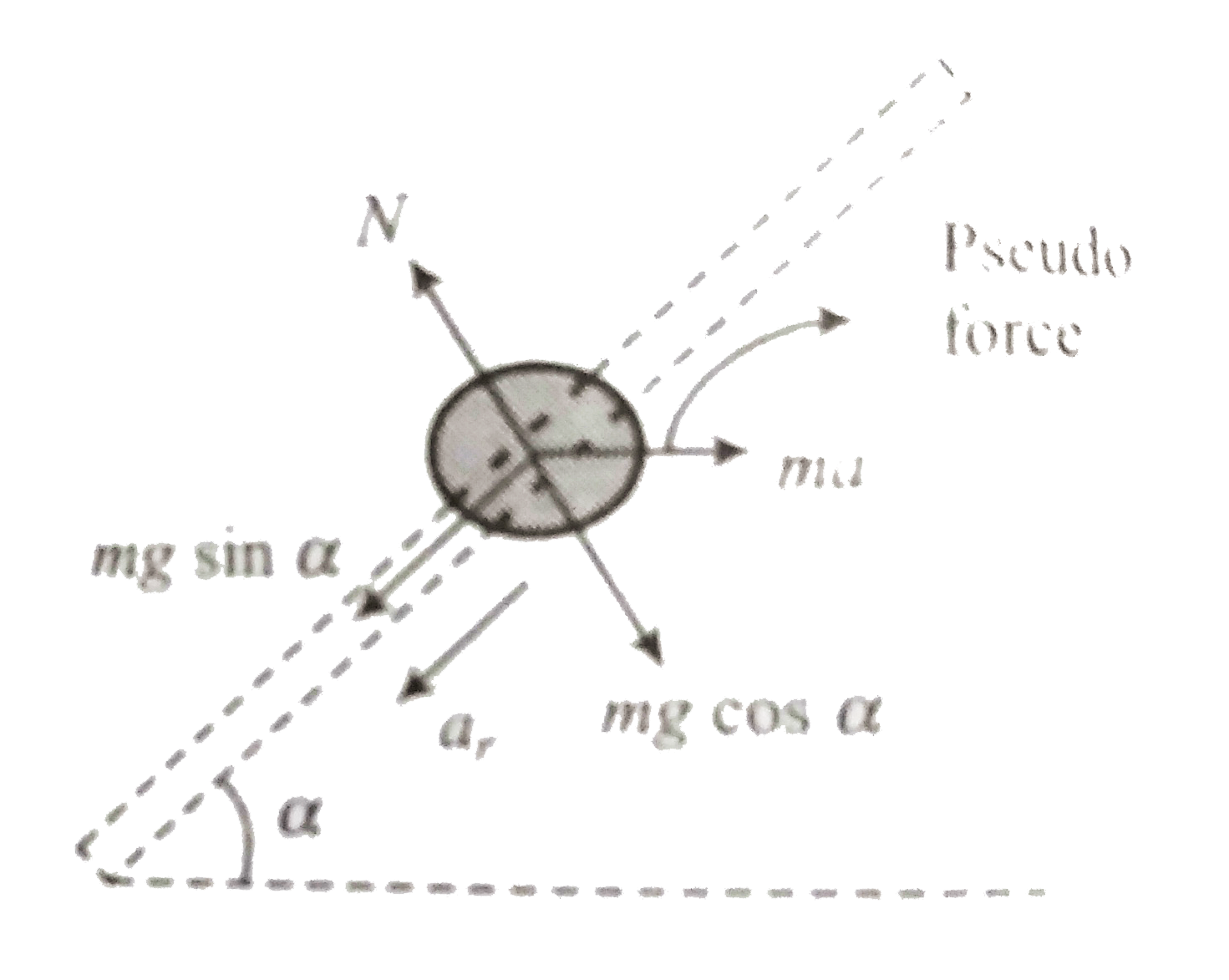
The bead is not moving perpendicular to rod. Hence,
N=mgcosα+masinα
Also in the direction along the rod, let acceleration of the bead w.r.t rod is ar.
Equation of motion of bead with rod,
mgsinα−macosα=mar
⇒ar=gsinα−acosα.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beada are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpenducular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionTwo balls of mass m and 4m are connected by a rod of length L. The mass of the rod is small and can be treated as zero . The size of the balls also can of the neglected . We also assume the centre of the rod is hinged ,but the rod can rotate about its centre in the vertical plane without friction . What is the gravity - induced angular acceleration of the rod when the angle between the rod and the vertical is θ as shown ?
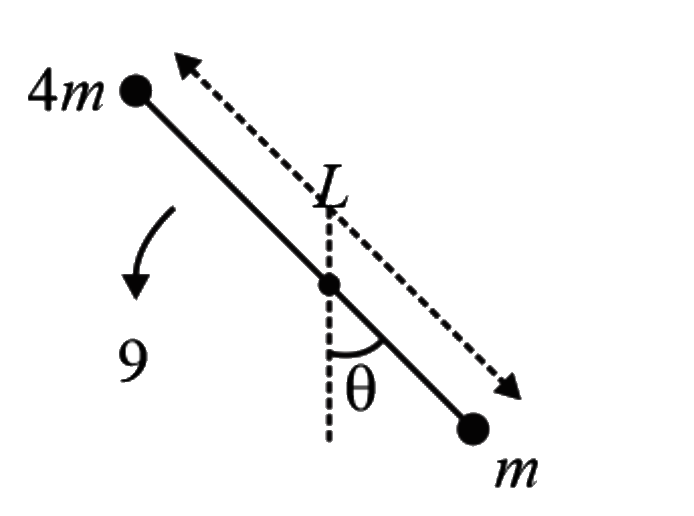
View Solution
Knowledge Check
A bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
 AgsinθB(g+a0)sinθCgsinθ+a0cosθDgsinθ−a0cosθ
AgsinθB(g+a0)sinθCgsinθ+a0cosθDgsinθ−a0cosθA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
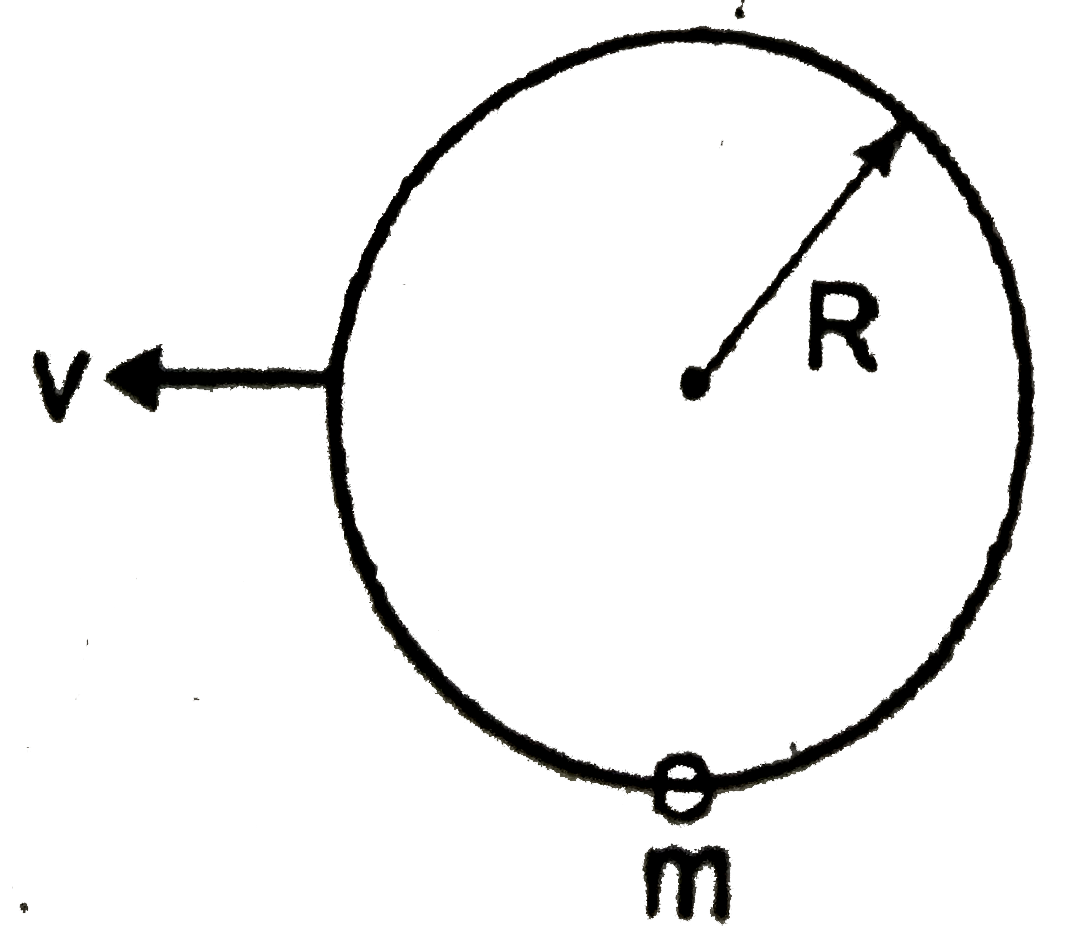 A√3gRB√4gRC√5gRD√5.5gR
A√3gRB√4gRC√5gRD√5.5gRA rod of mass 'm and length L is attached to a L shaped plank at 'A'. rod can move freely about A. A string is tied between rod and plank as shown in figure. Whole system is moving with a constant acceleration g in x-direction

If string is cut at any instant then the angular acceleration of rod (with respect to the plank) at that instant isA B
B C
C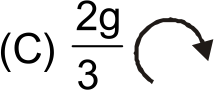 D
D
A rod touches a disc kept on a smooth horizontal plane. If the rod moves with an acceleration a, the disc rolls on the rod without acceleration a, the disc rools on therod without slidding. Then , the acceleration of the disc w.r.t the rod is

View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......

View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA rod of mass 'm and length L is attached to a L shaped plank at 'A'. rod can move freely about A. A string is tied between rod and plank as shown in figure. Whole system is moving with a constant acceleration g in x-direction
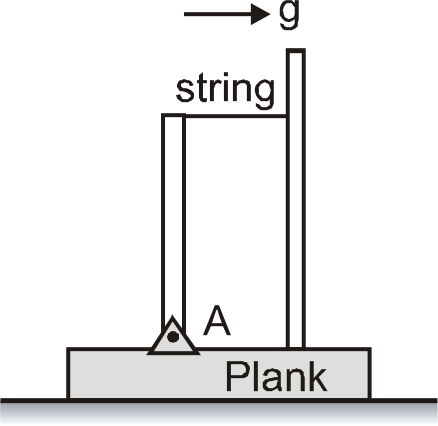
Force exerted by hinge on the rod is
View SolutionA ball of mass m moving with a speed u0 collides elastically with a rod of mass M suspended in the vertical plane by the hinge O. The rod is free to rotate in the vertical plane. Before and after the collision.
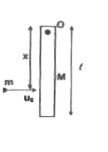
View Solution
