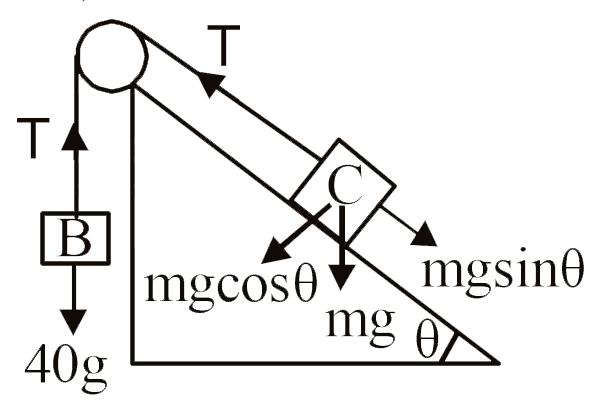
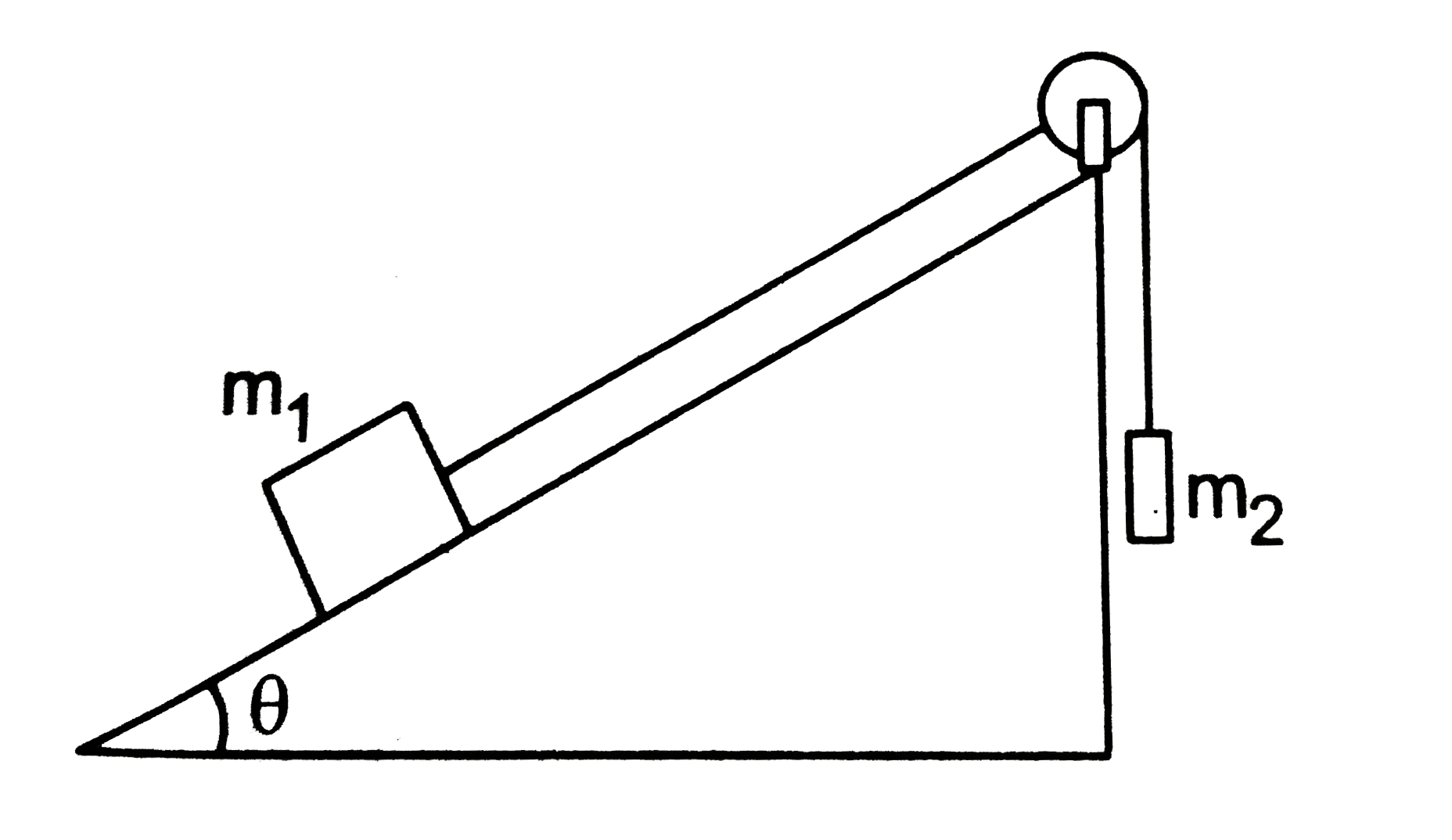
In fig.block A and B are connected together by a string and placed on a smooth inclined plane. B is connected to C(which is suspended vertically) by another string which passes over a smooth pulley fixed to th plane. The mass A is mA=1 kg and mass of B is mB=2kg.

(a) If the system is at rest, find the mass of C.
(b) If the mass of C is twice the mass calculate in (a) then find the acceleration of the system.
(a) From the free-body diagram of A :
T1: Tension in string betwwne A and B
NA: Normal reaction between A and incline
As A is at rest, net force parallel and perpendivular to inclined should be balanced.
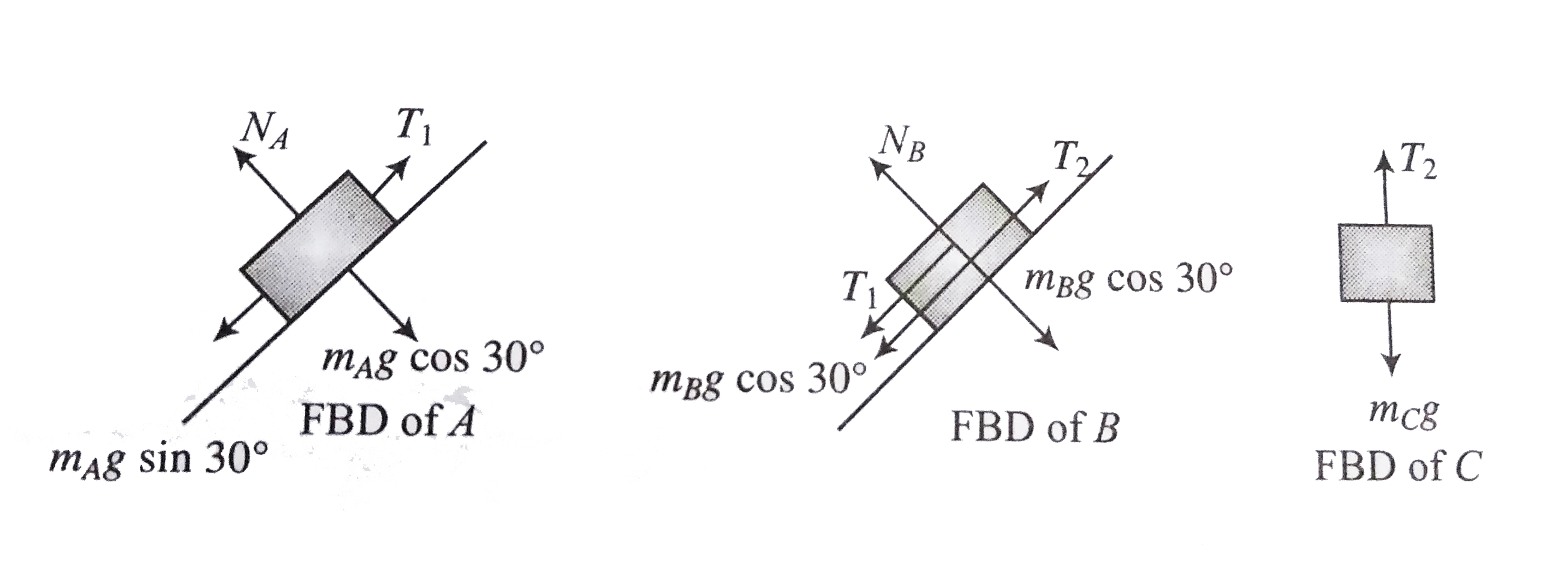
NA=mAgcosθ=10cos30∘=5√3N
T1=mAgsinθ=10sin30∘=5N
From the free-body diagram of B:
As B is connected to both strings, two tensions T1 and T2 will act on it.
T2 is the tension (force) of string between B and C acting upwards.
T1 is the tension of string between A and B acting downwards
Balancing forces:
NB=mBgcos30∘=20cos30∘=10√3N
T2=T1+mBgsin30∘=5+20sin30∘
=5+20×12=15N
Force diagram of C:
T2 is the pulling force of string on block C, therefore, mCg=T2, hence MC=1.5kg
(b) In this case, mass of C=3kg
Let the acceleration of the system be a. We can assume arbitrary direction of motion. Let the blocks move up the incline and block C move downward.
From FBD of A: T1−10sin30∘=1a ...(i)
From FBD of : T2−T1−20sin30∘=2a ...(ii)
From FBD of C: 30−T2=3a ...(iii)
Solving (i), (ii) and (iii) , a=2.5ms−2 .
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A body of mass 50kg resting on a smooth inclined plane is connected by a massless inextensible string passing over a smooth pulley, at the top of the inclined plane have another mass of 40 kg as shown in the figure. The distance through which 50 kg mass fall in 4 sec will be - (The angle of the inclined plane is 30∘)
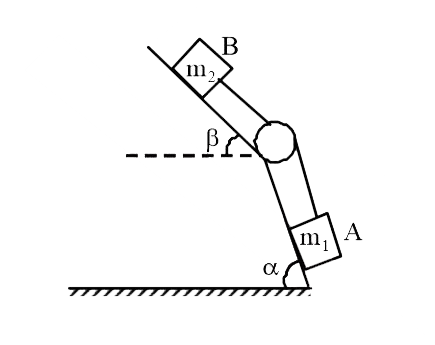
View SolutionTwo blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
View Solution
Knowledge Check
A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of masses is
A8:1B4:3C5:3D9:7A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A(a) 8:1B(b) 9:7C(c) 4:3D(d) 5:3A light string passing over a smooth light pulley connects two blocks of masses m1 and m2 (vertically). If the acceleration of the system is g/8, then the ratio of the masses is
A8:1B9:7C4:3D5:3
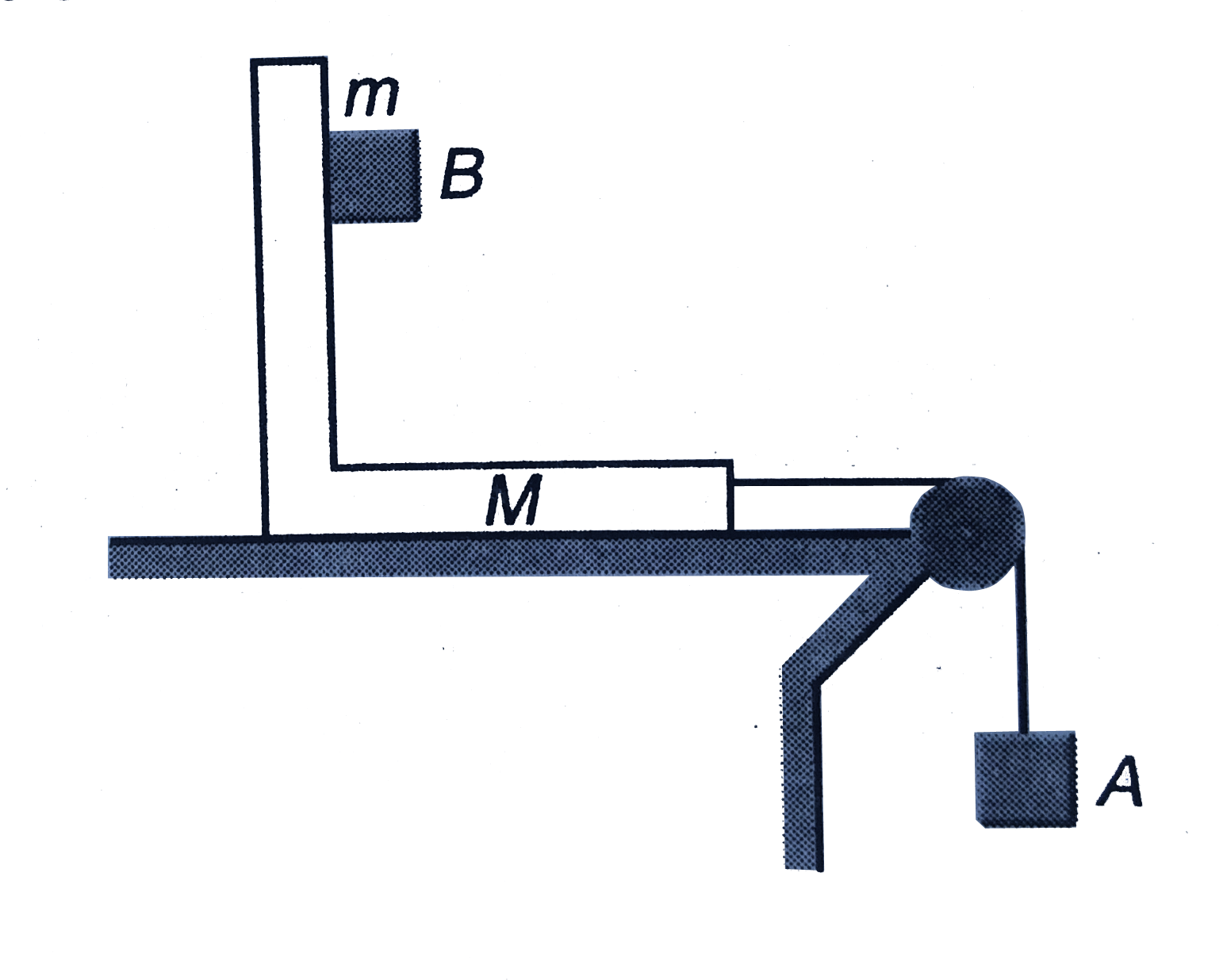
The figure an L shaped body of mass M placed on smooth horizontal surface. The block A is connected to the body by means of an inexiensible string , which is passing over a smooth pulley of negligible mass.Another block B of mass m is placed against a vertical wall of the body. Find the minimum value of the mass of block A so that B remain stationary relative to the wall. Coefficient of friction between the block B and the vertical wall is μ.
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
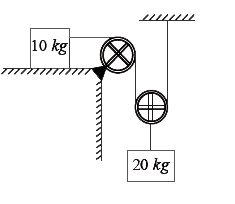
View SolutionTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View Solution
