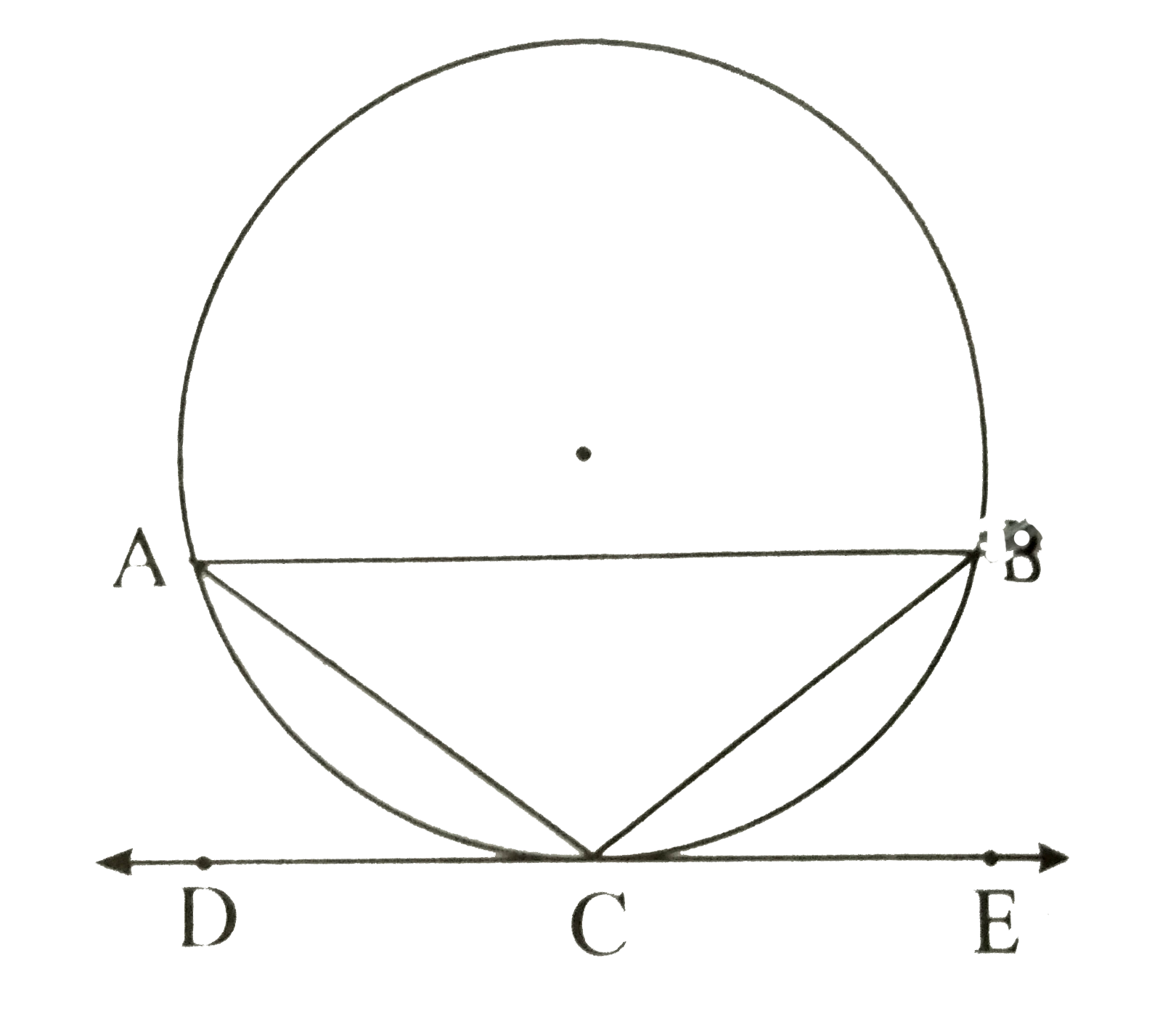
Two tangents AB and AC drawn from an external point A of a circle touch the circle at the point B and C .A tangent drawn a point X lies on minor are BC intersects AB and AC at the points D and E respectively. Prove that perimeter of ΔADE=2AB. Solution in Bengali
Let AB and AC are two tangents ddrawn from an external point A to the circle with centre O at the points B and C respectively.
∴AB=AC……..(1)
Similarly, DB=DxandEX=EC…..(2)
Now, perimeter of ΔADE=AD+DE+EA
=AD+(DX+EX)+EA [as per figure]
+AD+(DB+EC)+EA [from (2)]
=(AD+DB)+(AE+EC)
=AB+AC [as per figure]
AB+AB[∵AC=AB]=2AB.
Hence permeter of ΔADE=2AB. (Proved)

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
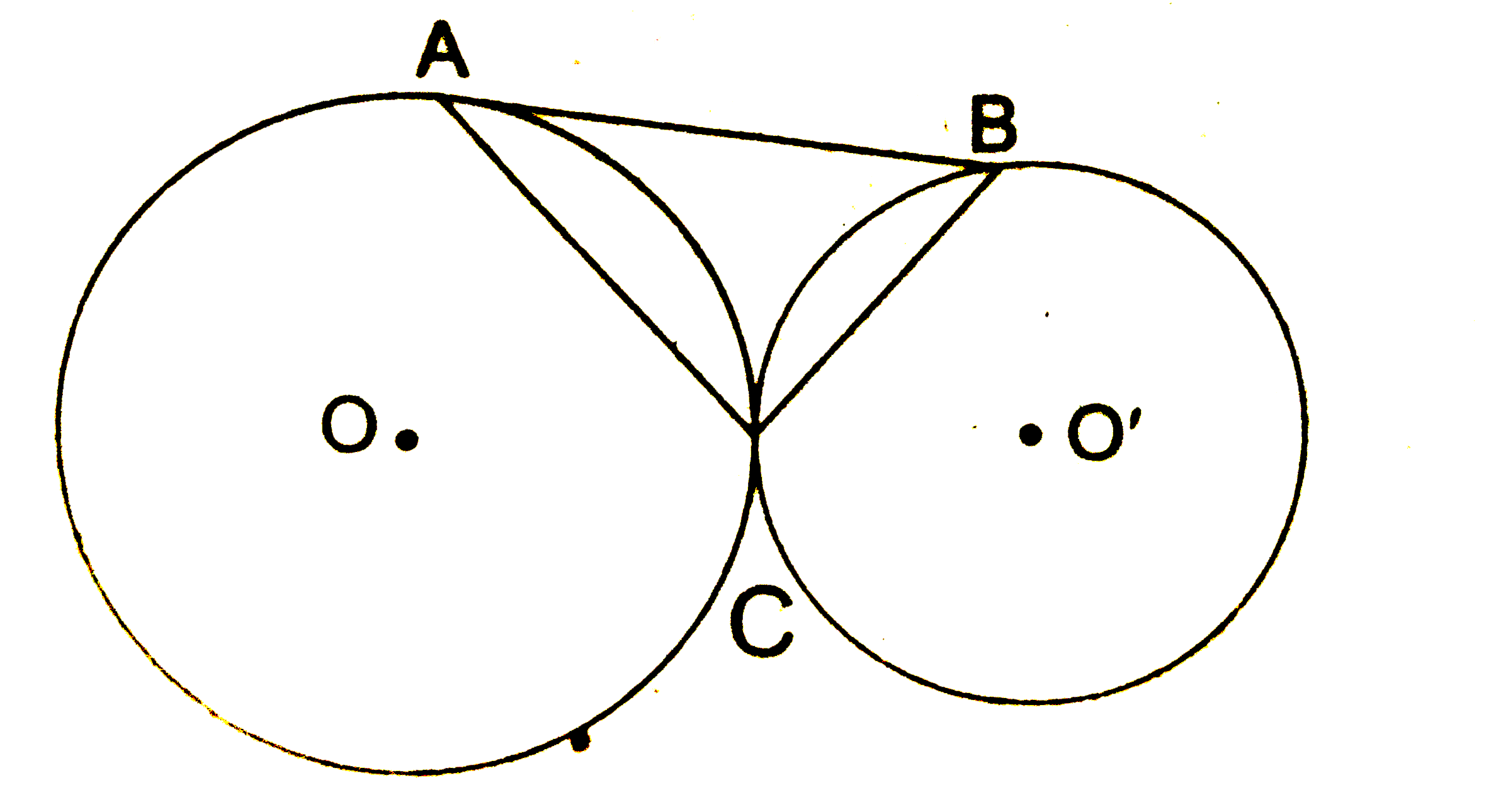
View SolutionTwo circles touch each other externally at point P.A common tangent AB is drawn touching the circles at A and B.Find /_APB .
View SolutionTwo circles are drawn with sides AB,AC of a triangle ABC as diameters. The circles intersect at a point D. Prove that D lies on BC.
View Solutionचित्र में O एवं O' केन्द्र के दो वृत्त एक-दूसरे का बाह्यतः बिन्दु C पर स्पर्श करते है। इन वृत्तों की एक उभयनिष्ठ स्पर्श रेखा AB खींची गई है। सिद्ध कीजिए कि ∠ACB=90∘
View SolutionIn the figure, chord AB∣∣ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
View SolutionThe tangent drawn from an extenral point A of the circle with centre C touches the circle at B. If BC=5cm,AC=13 cm, then the length of AB=
View SolutionTwo tangents are drawn from an external point A of the circle with centre at O which touches the circle at the points B and C. Prove that AO is the perpendicular bisector of BC.
View Solutionसमकोण त्रिभुज ABC क़ि भुजा AB को व्यास मानकर खींचा गया वृत्त कर्ण AC को P पर प्रतिच्छेद करता है सिद्ध कीजिये क़ि बिंदु P पर वृत्त क़ि स्पर्श रेखा भुजा BC को समद्विभाजित करती है।
View SolutionProve that if the two tangents drawn at the two points on the top of the circle intersect, then the lengths of the two straight lines drawn from the point of intersection to the point of tangent will be equal.
View SolutionTwo tangents AB and AC drawn from a point A outside of a circle touch the points B and C of the circle. The tangent intersects the tangent AB and AC at the points D and E, respectively, at the point X, located on the pressure BC. triangleADE Range of = 2AB.
View SolutionO কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ কর যে, BD^2=AD.DC
View Solutionदो वृत्त परस्पर P बिंदु पर बाह्यतः स्पर्श करते हैं और उभयनिष्ठ स्पर्श रेखाएं उन्हें A और B पर स्पर्श करती हैं तो सिद्ध कीजिए (i) P से खींची गई उभयनिष्ठ स्पर्श रेखाएं AB को समद्विभाजित करती है|
(ii) रेखा AB बिंदु P पर समकोण अंतरित करती है।
View Solution
