X is a point on the tangent at the point A lies on a circle with centre O.A secant drawn from a point X intersects the circle at the points Y and Z, If P is the mid-point of YZ, prove that XAPO or XAOP is a cyclic quadrilateral. . Solution in Bengali
XT is a tangent at A of the circle with centre at O. A secant XZ through X intersects the circel at the point Y and Z.P is the mid-point of YZ.
To prove : XAPOor XAOP is a cyclic quadrilateral.
Proof : YZ is a chord of the circle with centre at O and P is the mid-point of YZ ∴OP⊥YZ.
∴∠OPZ=90∘
Again XT is a tangent at A of the circle with centre at O.
∴OA⊥XT,∴∠OAX=90∘........(2)
Now, from (1) and (2) we get,
∠OPX+∠OAX=90∘+90∘=180∘
∴ Two opposite angles of the quadrilateral XAOP are supplementary.
∴XAOP is a cyclic quadrilateral. (Proved)

Topper's Solved these Questions
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.1
20 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
- TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE
66 Videos
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
View SolutionIf a point P is 17 cm from the centre of a circle of radius 8 cm, then find the length of the tangent drawn to the circle from point P.
View SolutionThrough a fixed point (h,k) secants are drawn to the circle x^(2)+y^(2)=r^(2). Then the locus of the mid-points of the secants by the circle is
View SolutionThrough a fixed point (h, k) secants are drawn to the circle x2+y2=a2 . The locus of the mid points of the secants intercepted by the given circle is
View SolutionP is any point on diameter of a circle with centre O.A perpendicular drawn on diameter at the point O intersects the point O intersects the circle at the point Q. Extended QP intersects the circle at the point R.A tangent drawn at the point R intersects extended OP at the point S. Prove theat SP=SR.[GP−X]
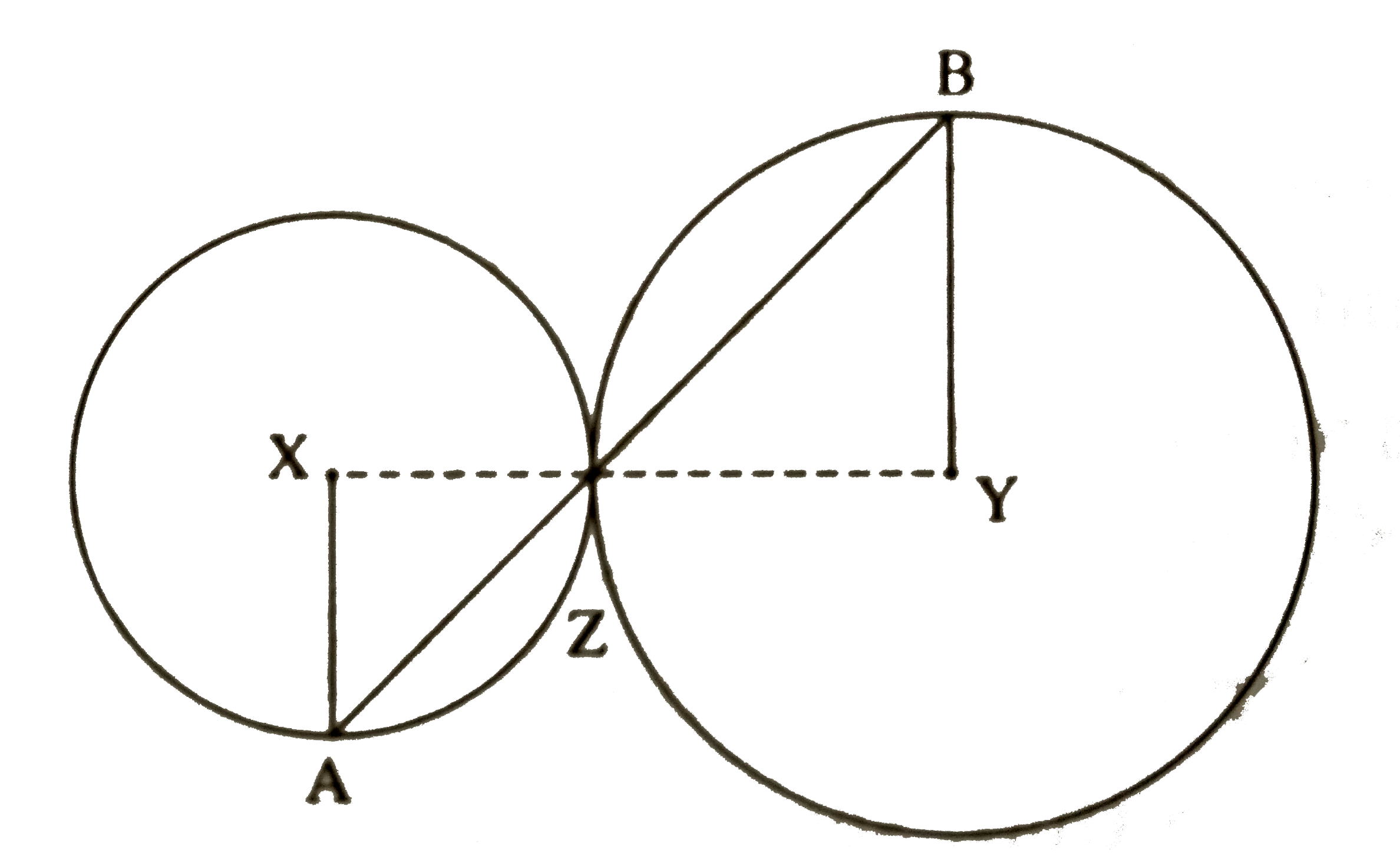
View SolutionIn the figure, circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, raduis XA || radius YB. Fill in the blanks and complete the proof:
View Solutionयदि एक चक्रीय चतुर्भुज ABCD के सम्मुख कोणों के समद्विभाजक इस चतुर्भुज के परिगत वृत्त को P और Q बिन्दुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि PQ इस वृत्त का व्यास है।
View SolutionP is a point outside a circle and is 13 cm away from its centre. A secant drawn from the point P intersects the circle at points A and B in such a way that PA=9 cm and AB=7 cm. The radius of the circle is
View SolutionXY of any circle is a diameter. Tangent to the PAQ circle at point A on the circle. The perpendicular drawn to the tangent of the circle from the point X intersects the PAQ at the point Z. Prove that XA, angleYXZ Isosceles of.
View SolutionO A point on the tangent to point A in a circle on a central circle. An intersection drawn from the point X intersects the circle at points Y and Z. If the midpoint of YZ is P, prove that XAPO or XAOP is a circular quadrilateral.
View SolutionProve that if the two tangents drawn at the two points on the top of the circle intersect, then the lengths of the two straight lines drawn from the point of intersection to the point of tangent will be equal.
View SolutionTwo tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
View Solution
