सिद्ध कीजिये कि समस्त त्रिभुजों के समुच्चय A में R = {(T1,T2):T1,T2 के समरूप है} द्वारा परिभाषित संबंध R एक तुल्यता संबंध है। भुजाओ 3, 4, 5 वाले समकोण त्रिभुज T1, भुजाओ 5, 12, 13 वाले समकोण त्रिभुज T2 तथा भुजाओ 6, 8, 10 वाले समकोण त्रिभुज T3 पर विचार कीजिये। T1,T2 और T3 में से कौन-से त्रिभुज परस्पर संबंधित है?
दिया गया है- R = {(T1,T2):T1,T2 के समरूप है T1,T2∈A} और जहाँ A समस्त त्रिभुजों का समुच्चय है।
स्वतुल्यता: माना T1∈A, तब T1 स्वयं के समरूप है क्योकि प्रत्येक त्रिभुज स्वयं के समरूप होते है।
⇒(T1,T1)∈R∀T1∈A
∴R,A में स्वतुल्य है।
सममितता: माना T1,T2∈A ऐसा है कि (T1,T2)∈R तब (T1,T2)∈R .
⇒T1,T2 के समरूप है।
⇒T2,T1 के समरूप है।
⇒(T2,T1)∈R∀T1,T2∈A
∴R,A में सममित है।
संक्रामकता: माना T1,T2,T3∈A ऐसा है कि (T1,T2)∈R और (T2,T3)∈R, तब
(T1,T2)∈R और (T2,T3)∈R
⇒T1,T2 के समरूप है और T2,T3 के समरूप है।
⇒T1,T3 के समरूप है।
⇒(T1,T3)∈R
∴R,A में संक्रामक है।
स्पष्टत: संबंध R, A में स्वतुल्य, सममित और संक्रामक है अत: R एक तुल्यता संबंध है।
द्वितीय भाग: त्रिभुज T1 की भुजाएं 3, 4, 5 है, त्रिभुज T2 की भुजाएँ 5, 12, 13 है तथा त्रिभुज T3 की भुजाएँ 6, 8, 10 है।
त्रिभुज T1 और T3 की भुजाएँ समानुपाती है अर्थात
36=48=510=12
∴T1,T3 के समरूप है।
⇒(T1,T3)∈R
⇒ त्रिभुज T1 और त्रिभुज T3 परस्पर संबंधित है।
Topper's Solved these Questions
- संबंध BOOK - PRABODH PUBLICATIONCHAPTER - संबंध EXERCISE - प्रश्नावली 1.1
12 Videos
- संबंध BOOK - PRABODH PUBLICATIONCHAPTER - संबंध EXERCISE - प्रश्नावली 1.2
8 Videos
- वर्धमान और ह्रासमान फलन BOOK - PRABODH PUBLICATIONCHAPTER - वर्धमान और ह्रासमान फलन EXERCISE - प्रश्नावली 15.2
37 Videos
- संबंध और फलन BOOK - PRABODH PUBLICATIONCHAPTER - संबंध और फलन EXERCISE - दीर्घ उत्तरीय प्रश्न
36 Videos
Similar Questions
माना समुच्चय A={1,3,5,7} में एक संबंध R इस प्रकार परिभाषित है कि R={(x,y):y=x+2}. संबंध R को क्रमित युग्मो के समुच्चय के रूप में लिखिए|
View Solutionसिद्ध कीजिये कि पूर्णको के समुच्चय Z में परिभाषित संबंध R,(a,b)∈R⇔a−b,5 से विभाज्य है, एक तुल्यता संबंध है।
View Solutionसिद्ध कीजिए कि फलन f(x)=x3−6x2+12x−18 पर एक निरंतर वधमान फलन है।
View Solutionसिद्ध कीजिए कि समुच्चय {1,2,} में R={(1,1),(2,2),(3,3),(1,2),(2,3)} द्वारा प्रदत्त संबंध स्वतुल्य है परन्तु न तो सममित है और न संक्रामक है।
View Solutionयदि एक वृत्त किसी समकोणीय अतिपरवलय से चार बिन्दुओं t1,t2,t3 तथा t4 में मिलता है, तो सिद्ध कीजिए कि t1,t2,t3,t4=1.
View Solutionसिद्ध कीजिए कि समस्त त्रिभुजो के समुच्यो A मै R={(T1,T2):T1,T2 के समरूप है। द्वारा परिभाषित संबंध R एक तुलयता संबंध है। भुजाओ 3, 4, 5 वाले समकोण त्रिभुज T1 भुजाओ 5, 12, 13 वाले समकोण त्रिभुज T2, तथा भुजाओं 6, 8 10 वाले सगकोण त्रिभुज T3 पर विचार कीजिए। T1,T2औरT3, में से कौन से त्रिभुज परस्पर संबंधित है?
View Solutionसिद्ध कीजिये की समस्त त्रिभुजों के समुच्चय A में, R={T1,T2}:T1,T2 के समरूप है, द्वारा परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T3 पर विचार कीजिये। T1,T2 और T3 में से कौन से त्रिभुज परस्पर संबंधित हैं?
View SolutionFind the sum of first 24 terms of on AP t1,t2,t3,...., if it is known that t1+t5+t10+t15+t20+t24=225.
View SolutionIf the sequence t1,t2,t3,… are in A.P. then the sequence t6,t12,t18,… is
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
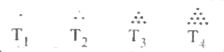
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View Solution
